Раздел IV
Дифференциальное исчисление функции двух переменных
Частные производные и дифференциал функции двух переменных.
Пусть имеем функцию двух независимых переменных  Геометрически эта функция описывает поверхность в трехмерной прямоугольной системе координат. Например, функция
Геометрически эта функция описывает поверхность в трехмерной прямоугольной системе координат. Например, функция  представляет собой уравнение параболоида вращения (рис. 4.1).
представляет собой уравнение параболоида вращения (рис. 4.1).
Предположим, что 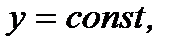 а переменная
а переменная  получает положительное приращение
получает положительное приращение  Тогда очевидно, что функция
Тогда очевидно, что функция  получает приращение только по
получает приращение только по  (см. рис. 4.1). Составим отношение частного приращения
(см. рис. 4.1). Составим отношение частного приращения 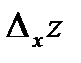 функции и приращения аргумента
функции и приращения аргумента  и перейдем к пределу при
и перейдем к пределу при  Если конечный такой предел существует, то он называется частным производным функции
Если конечный такой предел существует, то он называется частным производным функции  по переменной
по переменной  и обозначается так:
и обозначается так:
 (4.1)
(4.1)

Анологично определяется и частная производная по переменной  и обозначается так:
и обозначается так:
 (4.2)
(4.2)
Пример 4.1. Вычислить частные производные первого порядка функции 
Решение.


Ответ: 
Пример 4.2. Вычислить частные производные первого порядка функции 
Решение.

Ответ: 
Пример 4.3. Число рабочих на заводе увеличилось на 20%, а производительность труда каждого рабочего увеличилась на 40%. На сколько процентов увеличился обьем продукции?
Решение. Объем продукции есть функция двух независимых факторов (переменных), то есть  где
где  - количество рабочих, а
- количество рабочих, а 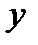 - производительность труда каждого
- производительность труда каждого
рабочего. При этом очевидно, что  После увеличения количества рабочих и производительности труда каждого рабочего на указанные в примере проценты новый объем продукции будет равен
После увеличения количества рабочих и производительности труда каждого рабочего на указанные в примере проценты новый объем продукции будет равен  где
где 
Тогда

Если теперь предположить, что  составляет
составляет  от
от  то будем иметь
то будем иметь 
Ответ: объем продукции увеличится на 
Пример 4.4. Издержки производства  зависият от двух независимых факторов (переменных)
зависият от двух независимых факторов (переменных)  и
и  по формуле
по формуле  Определить предельные издержки по каждому фактору.
Определить предельные издержки по каждому фактору.
Решение. Очевидно, чторешение сводится к нахождению частных производных функции  по переменным
по переменным  и
и  Итак имеем
Итак имеем

Ответ: предельные издержки по фактору  равны
равны  а по фактору
а по фактору 
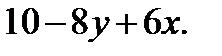
Определение 4.1. Если полное приращение 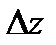 можно представить в виде
можно представить в виде
 (4.3)
(4.3)
где  при
при 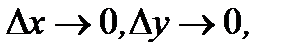 то функция
то функция  называется дифференцируемой. Главная линейная часть этого приращения называется дифференциалом функция
называется дифференцируемой. Главная линейная часть этого приращения называется дифференциалом функция  первого порядка, то есть
первого порядка, то есть
 (4.4)
(4.4)
Если теперь учесть, что  то из (4.4) для полного дифференциала первого порядка функции двух независимых переменных получим
то из (4.4) для полного дифференциала первого порядка функции двух независимых переменных получим
 (4.5)
(4.5)
Пример 4.5. Дано 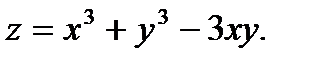 Найти
Найти 
Решение. Согласно (4.5) имеем

Ответ: 
Пример 4.6. Дано  . Найти
. Найти 
Решение. Согласно (4.5) имеем

Ответ: 
Пример 4.7. Дано  Найти
Найти 
Решение. Согласно (4.5) имеем
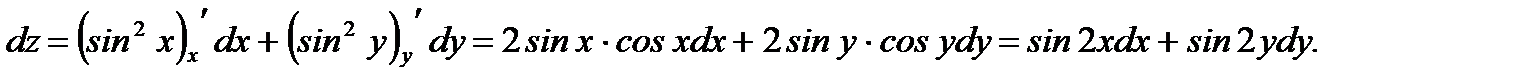
Ответ: 
Если вычислить частные производные от частных производных первого порядка функции  то получим частные призводные второго порядка функции
то получим частные призводные второго порядка функции  которые обозначаются следующим образом:
которые обозначаются следующим образом:

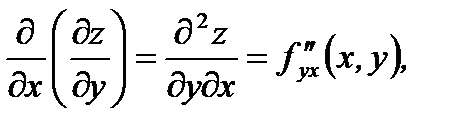 (4.6)
(4.6)
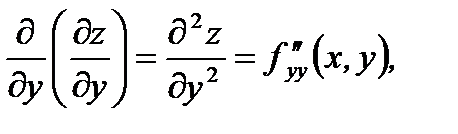
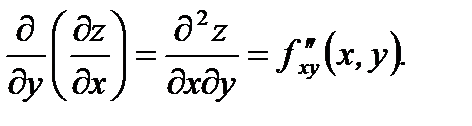 (4.7)
(4.7)
Теорема 4.1. Если смешанные производные второго порядка  и
и  являются непрерывными функциями по переменным
являются непрерывными функциями по переменным  , то они равны, то есть
, то они равны, то есть
 (4.8)
(4.8)
В случае независимых переменных  (
( ) и непрерывности частных производных второго порядка функции
) и непрерывности частных производных второго порядка функции  дифференциал второго порядка от функции
дифференциал второго порядка от функции  определяется следующим образом:
определяется следующим образом:
 (4.9)
(4.9)
Заметим, что принято символически (4.9) представить в виде
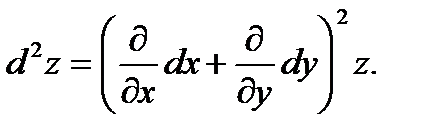
Пример 4.8. Дано  Найти
Найти 
Решение. Вычислим частные производные заданной функции двух независимых переменных и подставим в (4.9). Имеем

Ответ: 
Случаи сложной функции и функции, заданной в неявном виде.
Пусть функции  и
и  дифференцируемы по переменной
дифференцируемы по переменной  , а функция
, а функция
 дифференцируема в точке
дифференцируема в точке  Тогда можно доказать, что сложная функция
Тогда можно доказать, что сложная функция  дифференцируема по переменной
дифференцируема по переменной  и имеет место соотношение
и имеет место соотношение
 (4.10)
(4.10)
Аналогично, если  , и
, и 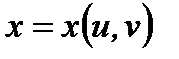 ,
,  , то имеют место следующие соотношения
, то имеют место следующие соотношения
 (4.11)
(4.11)
Теперь перейдем к случаю, когда функция двух независимых переменных  задана в неявном виде
задана в неявном виде  Тогда имеем
Тогда имеем
 (4.12)
(4.12)
Но с другой стороны
 (4.13)
(4.13)
Сравнивая (4.12) и (4.13), получим
 (4.14)
(4.14)
Пример 4.9. Дано:  Найти
Найти 
Решение. Согласно (4.6) имеем

Ответ: 
Пример 4.10. Дано  Найти
Найти 
Решение. Согласно (4.11) имеем


Ответ: 


Пример 4.11. Дано 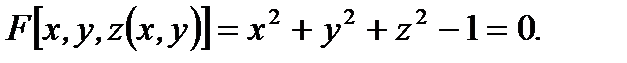 Найти
Найти 
Решение. Согласно (4.14) имеем

Ответ: 







