Математическая физика. Часть 2.
(курс предназначен для студентов физических специальностей ИФНИТ в осеннем семестре 3 курса)
Глава 1. Введение
1.1.  Предмет математической физики
Предмет математической физики
Основные задачи математической физики. Предметом математической физики является: постановка задач, вывод уравнений, определение граничных и начальных условий; классификация уравнении МФ, определение корректности задач; построение аналитических методов решения задач МФ; построение численных методов решения задач МФ, физическая интерпретация результатов. Основные обозначения в МФ.
1.2.  Декартовая, цилиндрическая и сферическая системы координат
Декартовая, цилиндрическая и сферическая системы координат
Характеристика радиуса вектора в декартовой системе координат  . Ортогональные орты в декартовой системе координат. Элемент поверхности
. Ортогональные орты в декартовой системе координат. Элемент поверхности  и элемент объема
и элемент объема  в декартовой системе координат. Правило суммирования Эйнштейна по дважды повторяющемуся индексу
в декартовой системе координат. Правило суммирования Эйнштейна по дважды повторяющемуся индексу  . Цилиндрическая система координат
. Цилиндрическая система координат  . Связь декартовых и цилиндрических компонент вектора
. Связь декартовых и цилиндрических компонент вектора  . Якобиан перехода от декартовой к цилиндрической системе координат. Элемент поверхности и элемент объема в цилиндрической системе координат. Площадь круга радиуса
. Якобиан перехода от декартовой к цилиндрической системе координат. Элемент поверхности и элемент объема в цилиндрической системе координат. Площадь круга радиуса  , величина боковой поверхности цилиндра, радиус которого равен
, величина боковой поверхности цилиндра, радиус которого равен  , а высота цилиндра равна
, а высота цилиндра равна  . Вычисление объема цилиндра
. Вычисление объема цилиндра  . Порядок интегрирования функций в цилиндрической системе координат. Связь декартовых компонент
. Порядок интегрирования функций в цилиндрической системе координат. Связь декартовых компонент  с компонентами вектора в сферической системе координат
с компонентами вектора в сферической системе координат  . Элементы поверхности и элементы объема в сферической системе координат. Якобиан перехода от декартовой к сферической системе координат. Поверхности сферы радиуса
. Элементы поверхности и элементы объема в сферической системе координат. Якобиан перехода от декартовой к сферической системе координат. Поверхности сферы радиуса  , объем сферы радиуса
, объем сферы радиуса  . Порядок интегрирования функций в сферической системе координат.
. Порядок интегрирования функций в сферической системе координат.
1.3  Скалярное произведение векторов. Евклидово пространство
Скалярное произведение векторов. Евклидово пространство
Определения скалярное произведение двух векторов. Символ Кронекера. Выражение скалярного произведения декартовых ортов через символ Кронекера. Выражение для скалярного произведения двух векторов с помощью правила суммирования Эйнштейна. Свойства символа Кронекера. Угол между двумя единичными векторами  и
и  , характеризующимися своими координатами в сферической системе координат
, характеризующимися своими координатами в сферической системе координат  и
и 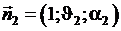 . Матрица перехода от ортов цилиндрической
. Матрица перехода от ортов цилиндрической  системы координат к ортам декартовой системы координат
системы координат к ортам декартовой системы координат  . Дифференцирование по времени ортов цилиндрической системы координат
. Дифференцирование по времени ортов цилиндрической системы координат 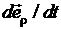 ,
, 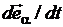 . Вычисление частных производных
. Вычисление частных производных  ,
,  ,
,  ,
,  . Матрица перехода от ортов cферической
. Матрица перехода от ортов cферической  системы координат к ортам декартовой системы координат
системы координат к ортам декартовой системы координат  . Вычисление частных производных
. Вычисление частных производных  ,
,  ,
,  ,
,  .
.  ,
,  . Пространство
. Пространство  , где
, где  – размерность пространства. Понятие евклидова пространства – конечномерного векторного пространства, в котором определено скалярное произведение. Скалярное произведение в евклидовом пространстве. Квадрат нормы вектора в
– размерность пространства. Понятие евклидова пространства – конечномерного векторного пространства, в котором определено скалярное произведение. Скалярное произведение в евклидовом пространстве. Квадрат нормы вектора в  – мерном евклидовом пространстве.
– мерном евклидовом пространстве.
1.4  Векторное, смешанное и двойное векторное произведение
Векторное, смешанное и двойное векторное произведение
Определение векторного произведения. Таблица векторного произведение декартовых ортов. Символ Леви-Чевита 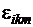 . Выражение для векторного произведения декартовых ортов через Символ Леви-Чивита. Смешанное произведение векторов. Двойное векторное произведение векторов. Доказательство свойств символов Леви-Чивита.
. Выражение для векторного произведения декартовых ортов через Символ Леви-Чивита. Смешанное произведение векторов. Двойное векторное произведение векторов. Доказательство свойств символов Леви-Чивита.
1.5  Тензорное исчисление
Тензорное исчисление
Поворот системы координат, где  –орты старой системы координат,
–орты старой системы координат,  –орты новой системы координат, повернутой относительно старой на некоторые углы. Условие ортогональности ортов
–орты новой системы координат, повернутой относительно старой на некоторые углы. Условие ортогональности ортов  в старой и новой системах координат
в старой и новой системах координат 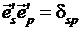 . Запись вектора
. Запись вектора  в старой системе координат
в старой системе координат  , и в новой системе координат
, и в новой системе координат 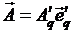 . Выражение для компонент вектора в новой системе координат
. Выражение для компонент вектора в новой системе координат  , через
, через  –косинусы углов между вектором
–косинусы углов между вектором  в новой системе координат, и вектором
в новой системе координат, и вектором  в старой системе координат. Вывод правил суммирования для косинусов
в старой системе координат. Вывод правил суммирования для косинусов  и
и  . Понятие инвариантности. Понятие скаляра, Понятие вектора (тензора 1 ранга). Понятие тензора 2 ранга. Понятие симметричного и антисимметричного тензора. Задача о произведении симметричного на антисимметричный тензор. Задача о инвариантности соотношений равенства между векторами и тензорами в старой и новой системах координат. Задача об инвариантности скалярного произведения. Закон связи двух векторов в анизотропной среде с помощью тензора 2 ранга. Задача об инвариантности шпура (суммы диагональных матричных элементов) тензора второго ранга.
. Понятие инвариантности. Понятие скаляра, Понятие вектора (тензора 1 ранга). Понятие тензора 2 ранга. Понятие симметричного и антисимметричного тензора. Задача о произведении симметричного на антисимметричный тензор. Задача о инвариантности соотношений равенства между векторами и тензорами в старой и новой системах координат. Задача об инвариантности скалярного произведения. Закон связи двух векторов в анизотропной среде с помощью тензора 2 ранга. Задача об инвариантности шпура (суммы диагональных матричных элементов) тензора второго ранга.
1.6. Векторный анализ в декартовой системе координат
Понятие скалярного поля  . Понятие поверхностей постоянного уровня для скалярного поля. Понятие плоской волны
. Понятие поверхностей постоянного уровня для скалярного поля. Понятие плоской волны  , где
, где  – волновой вектор,
– волновой вектор,  – радиус вектор, у которой фаза
– радиус вектор, у которой фаза  представляет собой уравнение плоскости. Понятие векторного поля
представляет собой уравнение плоскости. Понятие векторного поля  . Примеры скалярных и векторных полей в математической физике. Операция градиента для скалярного поля в декартовой системе координат. Оператор Гамильтона
. Примеры скалярных и векторных полей в математической физике. Операция градиента для скалярного поля в декартовой системе координат. Оператор Гамильтона  . Операция дивергенции вектора в декартовой системе координат. Операция ротора вектора в декартовой системе координат. Понятие оператора импульса
. Операция дивергенции вектора в декартовой системе координат. Операция ротора вектора в декартовой системе координат. Понятие оператора импульса 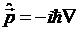 . Действие оператора импульса на плоскую волну
. Действие оператора импульса на плоскую волну  . Операции векторного анализа:
. Операции векторного анализа:  ,
,  ,
,  . Вид оператора Лапласа в декартовой системе координат
. Вид оператора Лапласа в декартовой системе координат  . Теорема Остроградского-Гаусса. Следствия из теоремы Остроградского Гаусса. Формула Грина. Теорема Стокса.
. Теорема Остроградского-Гаусса. Следствия из теоремы Остроградского Гаусса. Формула Грина. Теорема Стокса.
1.7. Криволинейные координаты. Операции  ,
,  ,
,  ,
,  в цилиндрической и сферической системах координат.
в цилиндрической и сферической системах координат.
Криволинейные координаты, Якобиан перехода от переменных  , Координатные поверхности
, Координатные поверхности 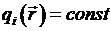 . Координатные линии – как линии пересечения двух координатных плоскостей. Квадрат элемента длины в декартовой системе координат. Квадрат элемента длины в цилиндрической системе координат (ЦСK). Определение коэффициентов Ламе в ортогональной системе координат. Коэффициенты Ламе в ЦСК. Выражение для градиента и для оператора Лапласа в ЦСК. Выражение для лапласиана в ЦСК системе координат, угловая часть, которого выражен через безразмерный оператор
. Координатные линии – как линии пересечения двух координатных плоскостей. Квадрат элемента длины в декартовой системе координат. Квадрат элемента длины в цилиндрической системе координат (ЦСK). Определение коэффициентов Ламе в ортогональной системе координат. Коэффициенты Ламе в ЦСК. Выражение для градиента и для оператора Лапласа в ЦСК. Выражение для лапласиана в ЦСК системе координат, угловая часть, которого выражен через безразмерный оператор  проекции момента, где оператор вектора момента импульса
проекции момента, где оператор вектора момента импульса  имеет вид
имеет вид  , где оператор импульса
, где оператор импульса 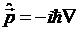 , оператор проекции момента импульса
, оператор проекции момента импульса  на оси
на оси  равен
равен  .
.
Выражения для градиента и лапласиана в произвольной ортогональной системе координат. Координатные поверхности и координатные линии в ЦСК. Квадрат элемента длины в сферической системе координат (ССК). Коэффициенты Ламе в (ССК). Выражения для градиента и оператора Лапласа в (ССК). Координатные поверхности и координатные линии в (ССК). Вывод выражения для оператора Лапласа в (ССК)  , где оператор
, где оператор 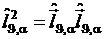 . Оператор
. Оператор  – представляет собой безразмерный оператор момента импульса.
– представляет собой безразмерный оператор момента импульса.
Глава 2. Специальные функции в математической физике
2.1.  Гамма и бета функция
Гамма и бета функция
Определение Гамма-Функции 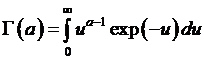 – интеграла Эйлера 2 рода. Условие сходимости Гамма-Функции при
– интеграла Эйлера 2 рода. Условие сходимости Гамма-Функции при  . Вывод выражения соотношения
. Вывод выражения соотношения 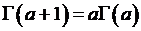 . Значения Гамма функции для целых значений аргумента. Выводы выражения
. Значения Гамма функции для целых значений аргумента. Выводы выражения  , где
, где  , величина
, величина  . Определение Бета функции (интеграл Эйлера 1 рода)
. Определение Бета функции (интеграл Эйлера 1 рода)  , где
, где  . Вывод соотношения
. Вывод соотношения  .
.
2.2 Формула Стирлинга. Объем сферы единичного радиуса в  мерном евклидовом пространстве
мерном евклидовом пространстве
Изложение метода перевала, использующегося для вычисления интеграла 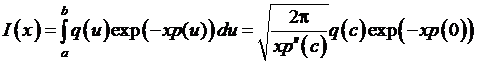 , где
, где 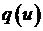 непрерывная функция, вещественный параметр
непрерывная функция, вещественный параметр  , и непрерывная функции
, и непрерывная функции  , имеет минимум в точке
, имеет минимум в точке  , где
, где  . Выражения для
. Выражения для  через Гамма функцию, где
через Гамма функцию, где  . Вычисление интеграла с Гамма функцией методом перевала для нахождения формулы Стирлинга
. Вычисление интеграла с Гамма функцией методом перевала для нахождения формулы Стирлинга  . Получение формулы для объема
. Получение формулы для объема  мерной сферы в евклидовом пространстве, имеющей радиус
мерной сферы в евклидовом пространстве, имеющей радиус  .
.
2.3. Интеграл вероятности и интеграл Досона
Определение интеграла вероятности  . Нечетность интеграла вероятности. Асимптотическое поведения интеграла вероятностей
. Нечетность интеграла вероятности. Асимптотическое поведения интеграла вероятностей  для
для  , и
, и  . График интеграла вероятности
. График интеграла вероятности  Явный вид полиномов
Явный вид полиномов  для
для  , удовлетворяющих соотношению
, удовлетворяющих соотношению  . Определение интеграла Досона
. Определение интеграла Досона 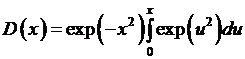 . График и асимптотика интеграла Досона
. График и асимптотика интеграла Досона  для
для  , и
, и  .
.
2.4.  Гильбертово пространство
Гильбертово пространство
Операторы в математической физике. Линейные операторы. Определение гильбертова пространства. Определение скалярного произведения комплексных функций в гильбертовом пространстве. Свойство скалярного произведения. Понятие нормы комплексной функции. Уравнения на собственные функции  и собственные значения
и собственные значения  оператора
оператора  :
:  . Ортогональность собственных функций. Орты гильбертова пространства
. Ортогональность собственных функций. Орты гильбертова пространства  . Разложение произвольной функции
. Разложение произвольной функции  в ряд по ортам гильбертова пространства
в ряд по ортам гильбертова пространства  :
: 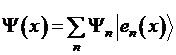 . Выражение для коэффициентов разложения
. Выражение для коэффициентов разложения  . Разложение функции
. Разложение функции  в ряд по ортогональной системе функций
в ряд по ортогональной системе функций  . Вывод выражения для коэффициентов разложения
. Вывод выражения для коэффициентов разложения  . Условие полноты базиса собственных функций в гильбертовом пространстве.
. Условие полноты базиса собственных функций в гильбертовом пространстве.
2.5 Операторы в гильбертовом пространстве
Единичный оператор. Произведение операторов, Обратный оператор. Комплексно сопряженные операторы  . Транспонированные операторы
. Транспонированные операторы  . Эрмитовски сопряженный оператор
. Эрмитовски сопряженный оператор  . Самосопряженные или эрмитовы операторы
. Самосопряженные или эрмитовы операторы  . Задача о нахождении собственных функций и собственных значений эрмитового оператора. Доказательство теоремы о вещественности собственных значений эрмитового оператора и о том, что собственные функции эрмитового оператора, отвечающие различным собственным значениям, ортогональны. Унитарный оператор. Задачи о транспонированном операторе
. Задача о нахождении собственных функций и собственных значений эрмитового оператора. Доказательство теоремы о вещественности собственных значений эрмитового оператора и о том, что собственные функции эрмитового оператора, отвечающие различным собственным значениям, ортогональны. Унитарный оператор. Задачи о транспонированном операторе 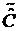 для оператора, представляющего собой произведение двух операторов
для оператора, представляющего собой произведение двух операторов  . Задача о доказательстве свойств эрмитовых операторов: оператора импульса
. Задача о доказательстве свойств эрмитовых операторов: оператора импульса 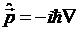 и оператора лапласиана
и оператора лапласиана  . Задача о собственных значениях унитарного оператора. Задача о инвариантности скалярного произведения унитарного оператора.
. Задача о собственных значениях унитарного оператора. Задача о инвариантности скалярного произведения унитарного оператора.
2.6.  Обобщенные функции математической физики. Дельта функция Дирака. Тета функция
Обобщенные функции математической физики. Дельта функция Дирака. Тета функция
Определение дельта функции  . Интеграл от произведения
. Интеграл от произведения  \ и непрерывной
\ и непрерывной  в симметричных пределах
в симметричных пределах  . Дельтаобразные последовательности
. Дельтаобразные последовательности  , зависящие от бесконечно малого параметра
, зависящие от бесконечно малого параметра  , которые моделируют дельта функцию
, которые моделируют дельта функцию  . Свойства
. Свойства  . Производная дельта функции. Ступенчатая Тета функция
. Производная дельта функции. Ступенчатая Тета функция  и ее связь с дельта функцией. Разложение
и ее связь с дельта функцией. Разложение  в интеграл Фурье. Фурье компонента дельта функции. Определение монохроматических волн – функций, зависящих от времени
в интеграл Фурье. Фурье компонента дельта функции. Определение монохроматических волн – функций, зависящих от времени  , представляющих собой колебание с фиксированной частотой
, представляющих собой колебание с фиксированной частотой  :
: 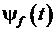 =
=  . Ортогональность двух монохроматических волн с различными частотами
. Ортогональность двух монохроматических волн с различными частотами  и
и  , выражающихся через дельта функцию. Трехмерная дельта функция
, выражающихся через дельта функцию. Трехмерная дельта функция  . Определение плоских волн – функций, зависящих от времени
. Определение плоских волн – функций, зависящих от времени  , с волновым вектором
, с волновым вектором  :
: 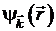 =
=  . Разложение трехмерной дельта функции
. Разложение трехмерной дельта функции  в интеграл Фурье. Ортогональность плоских волн с различными
в интеграл Фурье. Ортогональность плоских волн с различными  и
и  . Решение задачи о скалярном потенциале точечного заряда. Дельта функция в цилиндрической и сферической системах координат.
. Решение задачи о скалярном потенциале точечного заряда. Дельта функция в цилиндрической и сферической системах координат.
2.7. Ряды Фурье
Формулы разложения произвольной функции  в ряд по ортогональной системе функцию
в ряд по ортогональной системе функцию  . Введение безразмерных переменных для радиус векторов и моментов времени, которые позволяют свести задачу к безразмерной переменной
. Введение безразмерных переменных для радиус векторов и моментов времени, которые позволяют свести задачу к безразмерной переменной  , или к безразмерной переменной
, или к безразмерной переменной 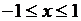 . Понятие рядов Фурье. Ортонормированность базиса тригонометрических функций
. Понятие рядов Фурье. Ортонормированность базиса тригонометрических функций  для
для  с весовой функцией
с весовой функцией  . Выражение для Фурье коэффициентов
. Выражение для Фурье коэффициентов  в этом базисе. Ортонормированность ортогональных функций
в этом базисе. Ортонормированность ортогональных функций  для
для 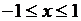 с весовой функцией
с весовой функцией 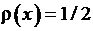 . Условия Дирихле для функции, имеющей точки разрыва. Теорема Дирихле о возможности разложения в ряд Фурье функции, удовлетворяющей условию Дирихле. Равенство Парсеваля, устанавливающее соответствие между квадратом нормы функции
. Условия Дирихле для функции, имеющей точки разрыва. Теорема Дирихле о возможности разложения в ряд Фурье функции, удовлетворяющей условию Дирихле. Равенство Парсеваля, устанавливающее соответствие между квадратом нормы функции  и суммой квадратов модулей Фурье коэффициентов
и суммой квадратов модулей Фурье коэффициентов  . Доказательство неравенства Бесселя, утверждающего, что возникающая погрешность между функцией
. Доказательство неравенства Бесселя, утверждающего, что возникающая погрешность между функцией  и аппроксимацией
и аппроксимацией  рядом Фурье с конечным количеством слагаемых, будет минимальна, при условии
рядом Фурье с конечным количеством слагаемых, будет минимальна, при условии 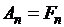 . Задачи на вычисление коэффициентов Фурье различных функций
. Задачи на вычисление коэффициентов Фурье различных функций  , где функция
, где функция  определяет знак переменной
определяет знак переменной 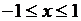 :
:  , если
, если  ;
;  , если
, если  ;
; 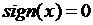 , если
, если  . Зависимость
. Зависимость  среднеквадратичного отклонения между
среднеквадратичного отклонения между  и
и  в зависимости от номера
в зависимости от номера  для различных
для различных  .
.
2.8.  Задача Штурма-Лиувилля о нахождении собственных значений и собственных функций уравнений математической физики
Задача Штурма-Лиувилля о нахождении собственных значений и собственных функций уравнений математической физики
Формулировка задачи Штурма-Лиувилля решения однородного дифференциального уравнения 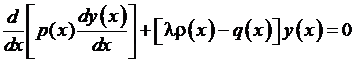 ,
,
где  – искомая функция,
– искомая функция,  – известные функции,
– известные функции,  –весовая функция. Понятие собственных значений
–весовая функция. Понятие собственных значений  и собственных функций
и собственных функций  . Простановка задач математической физики. Условия корректности Адамара. Классификация граничных задач уравнений математической физики: первая краевая задача (задача Дирихле); вторая краевая задача (задача Неймана); третья краевая задача (смешанная задача). Условие ограниченности решений
. Простановка задач математической физики. Условия корректности Адамара. Классификация граничных задач уравнений математической физики: первая краевая задача (задача Дирихле); вторая краевая задача (задача Неймана); третья краевая задача (смешанная задача). Условие ограниченности решений  для аргументов
для аргументов 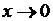 ,
,  . Начальные условия уравнений математической физики (задача Коши). Задача о нахождении собственных значений
. Начальные условия уравнений математической физики (задача Коши). Задача о нахождении собственных значений  и собственных функций
и собственных функций  одномерного стационарного уравнения Шредингера для частицы, помещенной в бесконечную потенциальную яму ширины
одномерного стационарного уравнения Шредингера для частицы, помещенной в бесконечную потенциальную яму ширины  , с граничными условиями для волновой функции
, с граничными условиями для волновой функции  ;
;  (задача Дирихле). Задача о разложении произвольной волновой функции
(задача Дирихле). Задача о разложении произвольной волновой функции  в бесконечной яме по собственным функциям
в бесконечной яме по собственным функциям  :
: 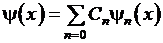 . Нахождение коэффициентов
. Нахождение коэффициентов  . Задача о нахождении собственных значений
. Задача о нахождении собственных значений  и собственных функций
и собственных функций  стационарного одномерного уравнения Шредингера для частицы, помещенной в потенциальную конечной высоты
стационарного одномерного уравнения Шредингера для частицы, помещенной в потенциальную конечной высоты  , причем ширина ямы равна
, причем ширина ямы равна  :
:  , если
, если  ;
;  , если
, если  .
.
2.9. Задача Штурма-Лиувилля для нахождения собственных значений и собственных функций стационарного одномерного уравнения Шредингера для частицы с энергией  , находящейся в потенциале
, находящейся в потенциале 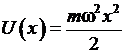 (задача гармонического осциллятора)
(задача гармонического осциллятора)
Поведение волновых функций 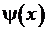 в различных потенциалах
в различных потенциалах  для инфинитного движения (непрерывный спектр собственных значений), полуфинитного движения и финитного движения (дискретный ряд собственных значений. Введения характерного масштаба изменения волновой функции
для инфинитного движения (непрерывный спектр собственных значений), полуфинитного движения и финитного движения (дискретный ряд собственных значений. Введения характерного масштаба изменения волновой функции  , безразмерной переменной
, безразмерной переменной  и приведение уравнения Шредингера для гармонического осциллятора к виду
и приведение уравнения Шредингера для гармонического осциллятора к виду  , где
, где  . Подстановка
. Подстановка 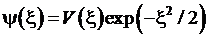 и дифференциальное уравнение для функции
и дифференциальное уравнение для функции  . Степенной ряд для функции
. Степенной ряд для функции  . Рекуррентные соотношения для коэффициентов степенного ряда. Условие ограниченности функции
. Рекуррентные соотношения для коэффициентов степенного ряда. Условие ограниченности функции  при
при  . Нахождение собственных значений
. Нахождение собственных значений  . Дифференциальное уравнение для полиномов Эрмита
. Дифференциальное уравнение для полиномов Эрмита  .
.
2.10. Свойство полиномов Эрмита
Вывод формулы Родрига для получения явного вида полиномов Эрмита  . Определение константы нормировки
. Определение константы нормировки  волновой функции
волновой функции 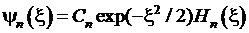 . Квадрат нормы полиномов Эрмита. Производящая функция для полиномов Эрмита. Вывод рекуррентных соотношений для полиномов Эрмита:
. Квадрат нормы полиномов Эрмита. Производящая функция для полиномов Эрмита. Вывод рекуррентных соотношений для полиномов Эрмита: 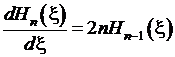 ,
,  . Задача: получить рекуррентные соотношения для нормированных волновых функций
. Задача: получить рекуррентные соотношения для нормированных волновых функций  задачи гармонического осциллятора. Задача: вычислить матричные элементы
задачи гармонического осциллятора. Задача: вычислить матричные элементы  операторов
операторов  =
=  по волновым функциям гармонического осциллятора
по волновым функциям гармонического осциллятора  . Задача об операторах рождения
. Задача об операторах рождения 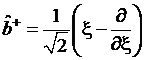 и уничтожения
и уничтожения  в квантовой задаче о гармоническом осцилляторе.
в квантовой задаче о гармоническом осцилляторе.
2.11. Полиномы Лежандра
Разложение 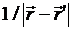 в ряд по полиномам Лежандра,
в ряд по полиномам Лежандра,  ,
, 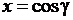 ,
,  – безразмерная переменная. Преобразование оператора
– безразмерная переменная. Преобразование оператора  . Явный вид полиномов Лежандра:
. Явный вид полиномов Лежандра:  ,
,  ,
,  . Ортогональность полиномов Лежандра. Переход от угловой части в операторе Лапласа, записанного в сферической системе координат, к безразмерной переменной
. Ортогональность полиномов Лежандра. Переход от угловой части в операторе Лапласа, записанного в сферической системе координат, к безразмерной переменной  . Собственные функции
. Собственные функции  и собственные значения
и собственные значения  уравнения
уравнения  . Формула Родрига для полиномов Лежандра
. Формула Родрига для полиномов Лежандра  . Собственные значения
. Собственные значения 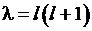 уравнения для полиномов Лежандра. Уравнения для производящей функции
уравнения для полиномов Лежандра. Уравнения для производящей функции  для полиномов Лежандра, в которых производящая функция равняется
для полиномов Лежандра, в которых производящая функция равняется 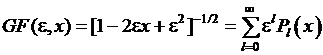 . Рекуррентные формулы для полиномов Лежандра, получающиеся из уравнений для производящей функции
. Рекуррентные формулы для полиномов Лежандра, получающиеся из уравнений для производящей функции  . Вычисление нормы для полиномов Лежандра. Аппроксимация произвольных функций
. Вычисление нормы для полиномов Лежандра. Аппроксимация произвольных функций  , заданной на интервале аргумента
, заданной на интервале аргумента 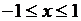 . Вычисление коэффициентов
. Вычисление коэффициентов 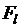 . Среднеквадратическая ошибка
. Среднеквадратическая ошибка  между функцией
между функцией  и ее аппроксимацией
и ее аппроксимацией  с помощью конечного ряда полиномов Лежандра
с помощью конечного ряда полиномов Лежандра  . Задача: аппроксимация функции
. Задача: аппроксимация функции  , вычисление коэффициентов
, вычисление коэффициентов  . Нахождение
. Нахождение  .
.
2.12 Присоединенные полиномы Лежандра. Сферические гармоники
Нахождение собственных чисел  и собственных функций
и собственных функций  уравнения
уравнения  для целых значений
для целых значений  и условиях ограниченности функции
и условиях ограниченности функции  . Случай
. Случай 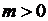 . Использование подстановки
. Использование подстановки  для получения дифференциального уравнения для
для получения дифференциального уравнения для  :
:  . Доказательство того, что уравнению для
. Доказательство того, что уравнению для  удовлетворяют присоединенные полиномы Лежандра
удовлетворяют присоединенные полиномы Лежандра  , где
, где  полиномы Лежандра, а собственные числа
полиномы Лежандра, а собственные числа 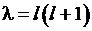 . Доказательство соотношения
. Доказательство соотношения  . Ортогональность присоединенных полиномов Лежандра
. Ортогональность присоединенных полиномов Лежандра  и
и  одинаковым значением
одинаковым значением  и различными значениями
и различными значениями  и
и  .
.
2.13. Метод Фурье. Разделение переменных в уравнении Лапласа в сферической системе координат
Метод разделения переменных (метод Фурье) для стационарного уравнения Шредингера. Фундаментальное решение для уравнения Лапласа  в случае сферической симметрии
в случае сферической симметрии  . Разделение переменных для уравнения Лапласа
. Разделение переменных для уравнения Лапласа  в случае, если функция
в случае, если функция  имеет азимутальную симметрию и не зависит от угла
имеет азимутальную симметрию и не зависит от угла  . Разделение переменных в уравнении Лапласа, в случае, если функция
. Разделение переменных в уравнении Лапласа, в случае, если функция 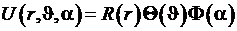 . Однозначные собственные функции оператора
. Однозначные собственные функции оператора  . Уравнение для функции
. Уравнение для функции  . Ортонормированные сферические гармоники
. Ортонормированные сферические гармоники 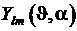 и их ортогональность. Оператор Лапласа в сферической системе координат
и их ортогональность. Оператор Лапласа в сферической системе координат  , где оператор
, где оператор 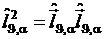 . Сферические гармоники
. Сферические гармоники 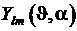 , как собственные функции уравнений
, как собственные функции уравнений  ,
,  . Явный вид сферических гармоник
. Явный вид сферических гармоник  ,
,  ,
,  ,
, 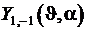 . Общее решение уравнения
. Общее решение уравнения  для функции
для функции 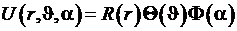 . Теорема сложения для сферических гармоник
. Теорема сложения для сферических гармоник  . Задачa об определении скалярного потенциала во всем пространстве, если существует идеально проводящая сфера радиуса
. Задачa об определении скалярного потенциала во всем пространстве, если существует идеально проводящая сфера радиуса  , на поверхности которой выполняется условие
, на поверхности которой выполняется условие  , а также точечный заряд
, а также точечный заряд  , находящейся на оси
, находящейся на оси  в точке
в точке  . Задача об определении скалярного потенциала во всем пространстве от сферы радиуса
. Задача об определении скалярного потенциала во всем пространстве от сферы радиуса  , помещенной в начало координат, поверхность которой заряжена с поверхностной плотностью
, помещенной в начало координат, поверхность которой заряжена с поверхностной плотностью  .
.
2.14 Разделение переменных в уравнении Лапласа в цилиндрической системе координат. Решение задачи Дирихле для круга
Уравнение Лапласа в цилиндрической системе координат. Фундаментальное решение для уравнения Лапласа 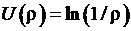 . Разделение переменных в уравнении Лапласа для задач, имеющих трансляционную симметрию по оси
. Разделение переменных в уравнении Лапласа для задач, имеющих трансляционную симметрию по оси  :
:  Однозначные собственные функции
Однозначные собственные функции  , где
, где  –целое число. Ограниченные собственные функции
–целое число. Ограниченные собственные функции 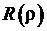 для внутренней задачи Дирихле (
для внутренней задачи Дирихле ( ). Ограниченные собственные функции
). Ограниченные собственные функции 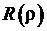 для внешней задачи Дирихле (
для внешней задачи Дирихле ( ). Граничное условие Дирихле на границе круга радиуса
). Граничное условие Дирихле на границе круга радиуса  :
:  , – где
, – где  – известная функция. Решение уравнения Лапласа во всем пространстве
– известная функция. Решение уравнения Лапласа во всем пространстве  , (
, ( и
и  ), удовлетворяющее условию Дирихле.
), удовлетворяющее условию Дирихле.
2.15. Полиномы Чебышева 1 и 2 рода
Общая характеристика полиномов Чебышева 1 и 2 рода. Явный вид полиномов Чебышева 1 рода  для безразмерной переменной
для безразмерной переменной 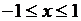 .Тригонометрическое выражения для полиномов Чебышева 1 рода
.Тригонометрическое выражения для полиномов Чебышева 1 рода  . Рекуррентные соотношения для полиномов Чебышева 1 рода. Квадрат нормы полиномов Чебышева 1 рода с весовой функцией
. Рекуррентные соотношения для полиномов Чебышева 1 рода. Квадрат нормы полиномов Чебышева 1 рода с весовой функцией  . Дифференциальное уравнение для полиномов Чебышева 1 рода. Рекуррентные соотношения для полиномов Чебышева 1 рода. Разложение произвольной функции
. Дифференциальное уравнение для полиномов Чебышева 1 рода. Рекуррентные соотношения для полиномов Чебышева 1 рода. Разложение произвольной функции  в ряд по полиномам Чебышева 1 рода. Вычисление коэффициентов разложения
в ряд по полиномам Чебышева 1 рода. Вычисление коэффициентов разложения  . Среднеквадратичное отклонение
. Среднеквадратичное отклонение  между аппроксимируемой функцией
между аппроксимируемой функцией  и конечным рядом
и конечным рядом  . Полинома Чебышева 2 рода
. Полинома Чебышева 2 рода  . Основные их свойства. Ортогональность полиномов Чебышева 2 рода с весовой функцией
. Основные их свойства. Ортогональность полиномов Чебышева 2 рода с весовой функцией  . Задача об аппроксимации функции
. Задача об аппроксимации функции  с помощью конечного ряда либо полиномов Чебышева 1 рода, либо Полиномов Чебышева 2 рода. Вычисление коэффициентов
с помощью конечного ряда либо полиномов Чебышева 1 рода, либо Полиномов Чебышева 2 рода. Вычисление коэффициентов  и среднеквадратичных отклонений
и среднеквадратичных отклонений 
2.16. Функции Бесселя вещественного аргумента  с целочисленным индексом
с целочисленным индексом 
Разложение функции  в ряд Фурье
в ряд Фурье  . Нахождения дифференциального уравнения для функции
. Нахождения дифференциального уравнения для функции  :
:  . Доказательство линейной зависимости между функциями Бесселя с положительным и отрицательным индексом
. Доказательство линейной зависимости между функциями Бесселя с положительным и отрицательным индексом  :
:  . Доказательство явного вида производящей функции
. Доказательство явного вида производящей функции  для функции Бесселя:
для функции Бесселя:  . Рекуррентные соотношения для функций Бесселя. Представление функции Бесселя с целочисленным индексом в виде бесконечных степенных рядов. Явный вид функций Бесселя
. Рекуррентные соотношения для функций Бесселя. Представление функции Бесселя с целочисленным индексом в виде бесконечных степенных рядов. Явный вид функций Бесселя 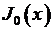 и
и  . Доказательство теоремы о асимптотическом вычислении сильно осциллируемых интегралов с помощью метода стационарной фазы
. Доказательство теоремы о асимптотическом вычислении сильно осциллируемых интегралов с помощью метода стационарной фазы  для
для  , причем
, причем 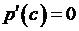 ,
,  , где точка
, где точка  удовлетворяет условию
удовлетворяет условию  . Асимптотическое значение
. Асимптотическое значение  :
:  . Нахождение асимптотики Бесселевской функции
. Нахождение асимптотики Бесселевской функции  с помощью метода стационарной фазы.
с помощью метода стационарной фазы.
2.17. Функции Бесселя с произвольным значением индекса 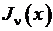
Уравнение для функций Бесселя 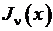 c нецелочисленным индексом
c нецелочисленным индексом  :
:  . Степенные ряды для функций
. Степенные ряды для функций 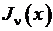 и
и  . Асимптотика поведения
. Асимптотика поведения 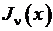 и
и  для малых
для малых  и больших значений
и больших значений  аргумента
аргумента  . Общее решение уравнения Бесселя
. Общее решение уравнения Бесселя  с нецелочисленным значением индекса
с нецелочисленным значением индекса  . Функция Бесселя второго рода
. Функция Бесселя второго рода  . Второе линейно независимое решение уравнения Бесселя для целочисленных значений
. Второе линейно независимое решение уравнения Бесселя для целочисленных значений  :
:  . Общее решение уравнений Бесселя
. Общее решение уравнений Бесселя  с целочисленным значением индекса
с целочисленным значением индекса  . Асимптотика поведения
. Асимптотика поведения  при
при  , асимптотика
, асимптотика  при
при  . Функции Ханкеля первого рода
. Функции Ханкеля первого рода 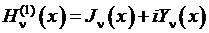 и второго рода
и второго рода  . Асимптотики
. Асимптотики  и
и  при
при  .
.
2.18. Функции Бесселя полуцелого аргумента 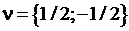 для вещественного аргумента
для вещественного аргумента  . Уравнение для функций Бесселя комплексного аргумента
. Уравнение для функций Бесселя комплексного аргумента  .
.
Функции Бесселя полуцелого индекса 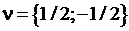 для вещественного аргумента
для вещественного аргумента  . Подстановка
. Подстановка  , которая приводит уравнение для функций Бесселя с индексом
, которая приводит уравнение для функций Бесселя с индексом  :
:  к дифференциальному уравнению
к дифференциальному уравнению  . Решения этого уравнения для
. Решения этого уравнения для 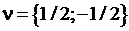 :
:  ;
;  .
.
Уравнение Бесселя для комплексного аргумента  :
:  . Введение функций
. Введение функций  ;
;  . Асимптотики поведения
. Асимптотики поведения  ,
,  при малых и больших значениях аргумента. Задача об интегральном представлении функции
при малых и больших значениях аргумента. Задача об интегральном представлении функции  и ее асимптотиках при
и ее асимптотиках при  и
и  .
.






