Пятигорская государственная фармацевтическая академия
Кафедра физической и коллоидной химии
Примеры задач с решениями
по физической и коллоидной химии
Для студентов II и III курсов
Пятигорск
2005
УДК
Авторы: доц. Л.П. Мыкоц, ст. преп. А.В. Погребняк, ст. преп. Е.И. Распопов
асс. С.Н.Бондарь, асс. Т.А.Савельева, асс. Т.Н.Сысоева,
асс. Н.Н.Степанова
Под общей редакцией
заведующего кафедрой физической и коллоидной химии,
доцента Л.П. Мыкоц
Рецензент: зав. кафедрой неорганической химии, профессор,
д.ф.н. В.А. Компанцев.
Утверждено на заседании ЦМС ПГФА «____»__________________2005 г.
Председатель ЦМС профессор Погорелов В.И.
Сборник типовых задач с решениями по физической и коллоидной химии для студентов 2,3 курсов очного и заочного отделений подготовлен на кафедре физической и коллоидной химии в соответствии с программой по дисциплине: физическая и коллоидная химия, Москва, 2002 год. Рекомендовано ЦМС ПГФА для подготовки студентов к сдаче экзамена и для выполнения контрольных работ студентов заочного отделения внутри академии
Предисловие
Навык решения задач является одной из самых важных составляющих образовательного процесса в разделе естественно-научных дисциплин. Решая задачи, студенты приобретают знания, необходимые для использования теории в практических целях. С учетом роста требований к практическим знаниям выпускников фармацевтических вузов и факультетов, обучение их методам и приемам расчетов выходит на первый план.
Настоящее пособие, не подменяя существующие учебники и сборники задач, предоставляет студентам фармацевтических факультетов очного и заочного отделений возможность достаточно быстро освоить приемы решения важнейших задач, включенных в действующую Учебную программу по физической и коллоидной химии, а также успешно подготовиться к заключительному экзамену.
В настоящий сборник задач по физической и коллоидной химии, подготовленный коллективом преподавателей кафедры физической и коллоидной химии Пятигорской ГФА вошли примеры решения типовых задач, в том числе:
по разделам физической химии - основы химической термодинамики, фазовые равновесия, электрохимия, кинетика химических реакций;
по разделам коллоидной химии - поверхностные явления, дисперсные системы, высокомолекулярные вещества.
Примеры решения задач по физической химии
Задача 1. Вычислите DНо, DUо, DGо и DА0 для реакции
2СО2(г) = 2СО (г) + О2 (г)
Определите, возможно ли самопроизвольное протекание реакции при стандартных условиях.
Решение: Воспользовавшись данными, приведенными в Приложении, рассчитаем тепловой эффект реакции при постоянном давлении:
DНоr = Sni DНof прод – Sni DНof исх =
= 2DНof CO + DНof O2 – 2DНof CO2 =
= [2(–110,70) + 0] – 2(–393,51) = 565,62 кДж/моль.
Изменение внутренней энергии связано с изменением энтальпии зависимостью: DUor = DHor – DnRT,
где: Dn – изменение числа молей газообразных веществ в ходе реакции,
Dn = 3 – 2 = 1;
R – универсальная газовая постоянная (8,314´10-3кДж/моль·К);
Т = 298К.
Следовательно:
DU0r = 565,62 – 8,314´10–3 ·298 = 563,14 кДж/моль.
Для расчета DGor найдем предварительно изменение энтропии:
DSor = 2SoСО + SoО2 – 2SoСО2 =
= (2´197,48+205,03) – 2´213,66 = 172,67 Дж/моль·К.
Tогда изменение энергии Гиббса будет равно:
DGоr = DНоr – ТDS0r = 565,62 – 298·172,67´10–3 = 514,16 кДж/моль.
Теперь определим изменение энергии Гельмгольца:
DАor = DUor – TDSor = 563,14–298·172,67´10–3 = 511,68 кДж/моль
Положительные значения величин DGor и DАor указывают на то, что при стандартных условиях реакция не будет самопроизвольно идти в прямом направлении.
Задача 2. Для реакции крекинга метана
СН4 (г) = С (т) + 2Н2(г) + ΔНr
Используя данные Приложения, рассчитать ΔG0r298 и ΔA0r298. Определить,
возможно ли самопроизвольное протекание данной реакции при температуре
298 К.
Решение:
1) Воспользовавшись данными Приложения
(ΔG0 f СН4 (г) = - 50,85; ΔG0 f С (т) = 0; ΔG0 f н2 (г) = 0 кДж/моль),
рассчитаем ΔG0r (изменение энергии Гиббса)
ΔG0r = åni ΔG0 f прод. - åni ΔG0 f исх. = ΔG0 f С (т) + 2 ΔG0 f н2 (г) - ΔG0 f СН4 (г) =
= 0 + 2× 0 – (-50,85) = +50,85 кДж
2) Для расчета ΔA0r воспользуемся соотношением между ΔG0r и ΔA0r:
ΔA0r = ΔG0r – ΔnRT,
где Δn – изменение числа молей газообразных веществ в ходе реакции,
R - универсальная газовая постоянная
Находим Δn: Δn = ånпрод. - ånисх. = 2 – 1 = 1
Отсюда:
ΔA0r = 50,89 - 1× 8,314 × 10-3 × 298 = 48,41 кДж,
т.к. ΔG0r298 и ΔA0r298 > 0, то при 298 К невозможно самопроизвольное протекание данной реакции в прямом направлении.
Задача 3. Для реакции крекинга метана
СН4 (г) = С (т) + 2Н2(г) + ΔНor
Рассчитать ΔН0r, используя значение стандартных теплот сгорания веществ (лДж/моль): ΔН0с СН4 (г) = - 890,31; ΔН0с С (т) = -393,51; ΔН0с Н2 (г) = -285,84
Определить экзо- или эндотермической является данная реакция.
Решение: В соответствии со следствием закона Гесса:
ΔН0r = åni ΔН0с исх. - åni ΔН0с прод. =
= ΔН0с СН4 (г) – (ΔН0с С (т) + 2 ΔН0с Н2 (г)) =
= -890,31 - [-393,51 + 2× (-285,84)] = +74,88 кДж
т.к. ΔН0r > 0, реакция является эндотермической.
Задача 4. Напишите уравнение реакции сгорания метана.Вычислите стандартную теплоту образования метана, если его стандартная теплота сгорания
ΔН0с = -890,31 кДж/моль
Продукты сгорания имеют следующие теплоты образования (кДЖ/моль)
ΔН0f СО2 (г) = -393,51; ΔН0f Н2О (ж) = -285,84
Решение:
Напишите термохимическое уравнение реакции сгорания метана
СН4 (г) + 2О2 (г) = СО2 (г) + 2Н2О (ж) + ΔН0r
В соответствии со следствием закона Гесса:
ΔН0r = åni ΔН0f прод. - åni ΔН0f исх. =
= (ΔН0f СО2 (г) + 2 ΔН0f Н2О (ж) ) – (ΔН0f СН4 (г) + 2× ΔН0f О2 (г))
С другой стороны: ΔН0r = ΔН0С СН4 (г)
Тогда: ΔН0с СН4 (г) = (ΔН0f СО2 (г) + 2 ΔН0f Н2О (ж)) – (ΔН0f СН4 (г) + 2 ΔН0f О2 (г) );
-890,31 = (-393,51 + 2× (-285,84)) – (ΔН0f СН4 (г) + 2 × 0);
- 890,31 = -393,51 – 571,68 - ΔН0f СН4 (г)
ΔН0f СН4 (г) = -74,88 кДж/моль.
Задача 5. Используя уравнение Кирхгоффа для небольшого температурного интервала рассчитать тепловой эффект реакции
СН3ОН(г)+3/2О2(г)=СО2(г)+2Н2О(г)
при температуре 500К и давлении 1,0133´105 Па.
Решение: По данным приложения сначала рассчитываем тепловой эффект реакции при 298К:
DНоr 298 = (DНof CO2 + 2 DНof H2O) – (DНof CH3OH +3/2DНof О2) =
= (–393,51–2´241,8) –(–201,00 + 3/2´0) = –676,13 кДж/моль.
Зная DНоr 298, можно по уравнению Кирхгоффа рассчитать тепловой эффект реакции при 500К:
DНоr Т2 = DНоr Т1 + DСор(Т2 - Т1)
где DСор – изменение теплоемкости в ходе реакции. Его можно определить таким образом:
DСор = SniСрi прод. – SniСрi исх. =
= (СорСО2 + 2СорН2О) – (СорСН3ОН – 3/2 СорО2) =
= (37,11+2´33,56)–(43,9–3/2´28,83) = 17,10 Дж/моль•К
и значит, тепловой эффект реакции при 500К равен:
DНor 500 = DНor 298 + DСор(500–298) =
= –676130 + 17,1´202 = –672676 Дж/моль = –672,676 кДж/моль.
Задача 6. Значение стандартной энергии Гиббса DGor реакции
СН3СООН(г)+С2Н5ОН(г)=СН3СООС2Н5(г)+Н2О(г)
равно –3,434 кДж/моль. Вычислите константы равновесия Кр и Кс. Каков будет состав равновесной реакционной смеси, если в реакцию введены 1 моль кислоты и 2 моля спирта?
Решение: Воспользуемся соотношением DGor = – RTlnKp, из которого получаем
DGor - 3,434
lnKp= – ¾¾¾¾ = – ¾¾¾¾¾¾¾ = 1,386
RT 8,314х10-3х298
и значит Кр = е1,386 = 3,9989» 4.
Кс = Кр(RT)–Dn, а так как Dn = 2 – 2 = 0, то Кс = Кр = 4.
Для того, чтобы ответить на вопрос о составе равновесной реакционной смеси, необходимо в общем виде проанализировать начальный и равновесный состав реакционной смеси:
| СН3СООН + С2Н5ОН = СН3СООС2Н5 + Н2О | ||||
| Исходный состав, моль | 1 | 2 | 0 | 0 |
| Равновесный состав, моль | 1–х | 2–х | х | х |
Выразим константу равновесия через равновесные количества молей веществ:
| х ·х Кс = ¾¾¾¾¾ = 4 (1–х)(2-х)
|
и решим уравнение относительно х:
х2=(1-х)(2-х)= 4; х2=(2–3х+х2)= 4; х2=8–12х+4х2; 3х2–12х+8=0
 D = Ö144–96=6,928; и значит
D = Ö144–96=6,928; и значит
| 12 + 6,928 12 – 6,928 х1 = ¾¾¾¾¾ = 3,15 моля; х2 = ¾¾¾¾¾ = 0,845 моля. 6 6 |
значение = 3,15 мол. х1 не имеет физического смысла (так как из 2 молей спирта нельзя получить 3 моля этилацетата) и отбрасывается. Таким образом, состав реакционной смеси при равновесии будет следующим:
уксусной кислоты: 1–0,845 = 0,155 моля,
спирта: 2–0,845 = 1,155 моля,
этилацетата: 0,845 моля,
воды: 0,845 моля.
Задача 7. Выразите известным вам способом концентрацию раствора 10 г NaCl в 100 мл (г) воды. В качестве способов выражения концентрации используйте:
1) молярную весовую концентрацию (моляльность);
2) молярную объемную концентрацию (молярность);
3) нормальность (молярную концентрацию эквивалента);
4) моляльную (молярную) долю;
5) титр;
6) весовой процент;
7) число граммов растворенного вещества на 100 г растворителя (коэффициент растворимости при данных условиях).
Решение:
|
Если обозначить:
Э - эквивалентный вес растворённого вещества;
M - молекулярный вес растворённого вещества;
MP - молекулярный вес растворителя;
n - число грамм-эквивалентов в 1 моль растворённого вещества;
p - плотность раствора, то:
nNaCl= mNaCl/MNaCl=10/23+35.5=0.17 моля;
nNaCl • m’H2O (1000 г) 0.17 • 1000
1) Сm = ----------------------------------- = -------------------- = 1,7 моль/1000 г;
mH2O 100
nNaCl • 1000 мл 0.17 1000
2) CM = ---------------------------- = --------------------- = 1,7 моль/л
100 мл (V H2O) 100
T • 1000
3) СN = ---------------- =; CN = 1,7 г экв/л
Э
также возможен расчет нормальности раствора по следующей формуле:
m X
СN = -----------------, где
Э 100
m – масса, г; X - массовая доля, %; Э - эквивалентная масса, г/г-экв.
nNaCl • n’H2O (1 моль) 0.17 1
4) N = --------------------------- = ----------------------; nр-ра = nNaCl + nH2O; N = 0,033
nр-ра 5+0.17
mNaCl • V’H2O (1 мл) 10 1
5) Т = ----------------------- = ------------------------; Т = 0,1 г/мл
V H2O 100
mNaCl 10
6) Р = ------------ = -------------; Р = 9,09 %
mH2O + mNaCl 100+10
7) А = mNaCl / m’H2O; А = 0,1 г/100 г воды
Задача 8. В 100 г воды растворено 1,53 г глицерина. Давление пара воды при 298К равно 3167,2 Н/м2. Вычислите: а) понижение давления пара воды над раствором; б) температуру кипения раствора; в) температуру его замерзания; г) его осмотическое давление.
Решение:
а) В соответствии с законом Рауля относительное понижение давления равновесного с раствором пара равно:
| ро – р Dр ¾¾¾¾ = ¾¾¾ = Хгл, ро ро
|
где Хгл – мольная доля глицерина в растворе.
Хгл = nгл/(nгл + nводы), где n – количество вещества (моль).
| nводы=100/18 = 5,555 моль; nгл = 1,53/92 = 0,017 моль;
|
Значит, Хгл= 0,017/(0,017 + 5,555) = 0,003,
и тогда Dр/3167,2 = 0,03; DР = 95,02 Па.
б) Повышение температуры кипения раствора неэлектролита можно вычислить по эбуллиоскопической формуле:
| Кэ m 1000 DТкип = ¾¾¾¾¾, M a
|
где Кэ – эбуллиоскопическая константа растворителя (для воды она равна 0,52); m – масса растворенного вещества в граммах; М – его молярная масса;
а – масса растворителя в граммах. Отсюда
| 0,52´1,53´1000 DТкип = ¾¾¾¾¾¾¾¾ = 0,086о. 92´100
|
Следовательно, температура кипения раствора будет равна 100,0860С.
в) Понижение (депрессия) температуры замерзания раствора рассчитывается по криоскопической формуле:
| Кк m 1000 DТзам = ¾¾¾¾¾, M a |
где Кк - криоскопическая константа растворителя (для воды 1,86):
| 1,86·1,53·1000 DТзам = ¾¾¾¾¾¾¾ = 0,309о 92·100
|
Следовательно, раствор будет замерзать при –0,309оС.
г) в соответствии с законом Вант–Гоффа осмотическое давление в растворах неэлектролитов можно рассчитать по уравнению
p = CRT,
где С – молярная концентрация раствора.
При пересчете в систему СИ концентрация должна быть выражена в моль/м3. Считая плотность раствора равной плотности воды, получим:
| 1,53·1000 С = ¾¾¾¾¾ = 0,17 моль/л = 0,17´103 моль/м3. 90·100 |
Тогда
p = 0,17´103·8,314·298 = 421187,2 Па (» 4,2 атм).
Задача 9.
Рассчитайте осмотическое давление водного раствора хлорида кальция с концентрацией 0,05 моль/л при температуре 370С. Степень диссоциации
(ионизации) CaCl2 равна 97%. Каким этот раствор является по отношению к плазме крови: гипо-, гипер- или изотоническим?
Решение:
Осмотическое давление растворов электролитов рассчитывается по уравнению Вант - Гоффа:
pосм = iCRT,
где i - изотонический коэффициент Вант – Гоффа
С – концетрация раствора (моль/л, моль/м3)
R – универсальная газовая постоянная
Т – температура, К
Расчет i: i = 1 + a(n - 1),
где a - кажущаяся степень диссоциации электорлита
n - число частиц (ионов), на который диссоциирует молекула
электролита СаСl2 «Са2+ + 2Сl-
(n = 3); i = 1 + 0,97(3 – 1) = 1 + 1,94 = 2,94
pосм = iCRT = 2,94 × 0,05 × 0,082 × 310 = 3,74 атм.
или: pосм = 2,94 × 0,05 × 103 × 8,314 × 310 = 378868,98 p а
т.к. pосм р. СаСl2 = 3,74 атм < pосм плазмы крови (7,6 атм)
Следовательно этот раствор гипотонический.
Задача 10. Из 1 л водного раствора, содержащего 1 г иода, иод экстрагируют сероуглеродом. Коэффициент распределения иода между водой и сероуглеродом равен 0,0017. Рассчитайте:
а) массу иода, оставшегося в водном растворе после одной операции экстрагирования объемом 40 мл экстрагента;
б) массу иода, оставшегося в водном растворе после 4-х кратного экстрагирования порциями по 10 мл сероуглерода;
в) массу иода, которая извлечется сероуглеродом в случаях (а) и (б);
г) степень извлечения иода в случаях (а) и (б);
д) число операций экстрагирования порциями по 10 мл сероуглерода, необходимых, чтобы извлечь из водного раствора 97% иода.
Решение.
а) Воспользуемся уравнением для однократной экстракции:
| KV1 1·0,0017·1000 m1 = m0 ¾¾¾¾ = ¾¾¾¾¾¾¾ = 0,041 г, KV1+V2 0,0017·1000+40 |
где К – коэффициент распределения растворенного вещества;
m0 – масса иода (г) в исходном водном растворе;
m1 – масса иода, оставшегося в водном растворе (рафинате) после
однократной операции экстрагирования;
V1 – объем исходного водного раствора (мл);
V2 – объем экстрагента (мл) в одной операции экстрагирования.
б) В случае многократной экстракции в рафинате остается
|
m = m0 -------- = 1· ---------------- = 0,00044 г, KV1+V2 0,0017·1000+10 |
где n - число операций экстрагирования.
в) Перейдет в экстракт при четырехкратном экстрагировании
mэ = m0 - m = 1 - 0,00044 = 0,99956 г.
|
m = m0 [1– ¾¾¾¾ ] = 1· [1 - ¾¾¾¾¾¾¾ ] = 0,99956 г KV1+V2 0,0017·1000 + 10
|
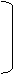
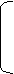 Массу экстрагированного вещества можно рассчитать и с помощью другого уравнения:
Массу экстрагированного вещества можно рассчитать и с помощью другого уравнения:
г) Степень извлечения вычислим как отношение массы иода, перешедшего в экстракт, к массе его в исходном водном растворе. В первом случае:
a1 = (1–0,041)/1 = 0,959 или 95%;
во втором случае:
a2 = 0,99956/1 = 0,99956 или 99,956%.
д) Число экстракций для достижения заданной степени извлечения при V2=10 мл, найдем с помощью уравнения, использованного в п. (в):
| KV1 n a = mэ/m0 = 1 – (¾¾¾¾); 0,97 = 1 – 0,145n; 0,03 = 0,145n. KV1+V2 |
Отсюда
lg 0,03 = n lg 0,145; n = lg 0,03/lg 0,145 = (-1,5229/-0,8386) =1,82.
Т.е. число экстракций равно двум (1,82»2).
Задача 11. Вычислить давление, необходимое для понижения температуры замерзания воды на 1о, и температуру, при которой будет плавиться лед при повышении давления на 1 атм. При 0оС удельная теплота плавления льда равна 333,5´103 Дж/кг, плотность воды 0,9998´103 кг/м3, плотность льда 0,9168´103 кг/м3.
Решение: Используем уравнение Клапейрона для фазовых превращений в однокомпонентных системах:
| Dр L ¾ = ¾¾¾ DТ T DV
|
где Dр/DТ – изменение давления фазового превращения при изменении температуры на 1 градус; L – удельная теплота фазового превращения при температуре Т; DV = (Vж – Vтв) – изменение удельного объема при фазовом переходе.
Удельные объемы – величины обратные плотности, следовательно:
Vж=1/9,998´102=1,0002´10–3 м3/кг;
Vтв=1/9,168´102=1,0908´10–3 м3/кг;
и DV=1,0002´10–3 – 1,0908´10–3 = –9,06´10–5 м3/кг;
| Dр 333,5´103 ¾¾ = ¾¾¾¾¾¾¾ = –134,8´105 Па/К DТ 273(–9,06´10–5) |
Знак «минус» указывает на то, что для уменьшения температуры кристаллизации воды (или плавления льда) давление должно быть повышено. Следовательно, для понижения температуры замерзания воды на 1оС необходимо давление повысить на 134,8´105 Па (или 133 атм), т.е. довести его до 134 атм.
Изменение температуры фазового перехода при изменении давления на единицу найдем с помощью преобразования уравнения:
| DТ 1 ¾¾ = ¾¾¾¾¾ = –0,0074´10–5 К/Па; DР –134,8´105
DТ 1 или ¾¾ = ¾¾¾ = –0,0075 К/атм; DР –133
|
Следовательно, при повышении давления на 1 атм температура плавления льда уменьшается на 0,0075К и становится равной -0,0075оС.
Задача 12. Рассчитайте количество водяного пара, необходимого для перегонки 10 кг анилина, если смесь анилина с водой при атмосферном давлении кипит при 98,4оС. При этой температуре давление водяного пара равно 94605 Па.
Решение. Коэффициент расхода пара mв/mа при перегонке с водяным паром рассчитывается по уравнению:
| mв рв Мв ¾¾ = ¾¾¾¾, mа ра Ма
|
где mв и mа –массы воды и анилина, Мв и Ма – молярные массы воды и анилина; рв и ра – парциальные давления паров воды и анилина при температуре перегонки.
ра находится с помощью закона Дальтона как разность между нормальным атмосферным давлением и рв:
ра = 101325 Па – 94605 Па = 6720 Па.
Отсюда:
| mв 94605·18 2,72 ¾¾ = ¾¾¾¾¾ = ¾¾¾ = 2,72 mа 6720·93 1
|
Следовательно, для перегонки 1 кг анилина требуется 2,72 кг водяного пара, а для 10 кг анилина его понадобится 27,2 кг.
Задача 13. Раствор, содержащий 0,8718 моль/л тростникового сахара, при Т = 291К, изотоничен с раствором хлорида натрия, содержащим 0,5 моль/л NaCl.Рассчитайте: а) изотонический и осмотический коэффициенты для хлорида натрия; б) кажущуюся степень его диссоциации.
Решение:
а) Для раствора сахара осмотическое давление рассчитывается по уравнению Вант-Гоффа для неэлектролитов: p1 = С1RT; а для раствора NaCl по уравнению для электролитов: p2 = iC2RT, где i -изотонический коэффициент. Так как осмотические давления растворов равны, т.е. p1 = p2, и значит С1RT = iC2RT.
Отсюда i = С1/С2 = 0,8718/0,5 = 1,7436.
По величине изотонического коэффициента рассчитываем осмотический коэффициент g:
g = i/n = 1,7436/2 = 0,8718,
где n– число ионов, образующихся при диссоциации одной молекулы.
б) Кажущуюся степень диссоциации a вычисляем с помощью уравнения, связавющего ее с изотоническим коэффициентом:
i = 1 + a(n –1);
Отсюда a = (i –1)/(n–1) = (1,7436 –1)/(2 –1) = 0,7436.
Задача 14. Для предотвращения частичного разложения лекарственного препарата в кипящем водном растворе при отгонке воды необходимо понизить температуру кипения на 20о. Вычислите, какое давление при этом надо поддерживать в перегонном аппарате. Теплота испарения воды
40660 Дж/моль.
Решение: Используем для расчета уравнение Клапейрона–Клаузиуса:
| р2 DНисп. (T2 – T1) ln ¾¾ = ¾¾¾¾ · ¾¾¾¾¾ р1 R T1·T2
|
Считая, что температура кипения раствора T2 при нормальном атмосферном давлении р2 = 101325 Па равна 100оС (373К), подставим значения:
| 101325 40660 (373 – 353) ln ¾¾¾¾ = ¾¾¾¾ · ¾¾¾¾¾¾ = 0,7428. р1 8,314 353·373
|
отсюда lnр1 = ln101325 – 0,7428 = 11,5261 – 0,7428 = 10,7832,
и значит, требуемое давление р1 = e10,7832 = 48204 Па (0,47 атм.).
Задача 15. Рассчитайте объемы 0,1 М растворов уксусной кислоты и ацетата натрия, необходимые для приготовления 20 мл ацетатного буферного раствора с рН = 4.
Решение. Так как концентрации растворов одинаковы, расчет ведется по уравнению:
| Vс.о. Сс.о. рН = рКа + lg ¾¾¾¾¾, Vс.к. Сс.к..
|
где рКа – показатель кислотности уксусной кислоты, равный 4,74;
Vс.о. и Vс.к. – соответственно объемы растворов сопряженных основания и кислоты. Отсюда при Сс.к. = Сс.о.:
lg Vс.о./Vс.к. = рН – рКа = 4 – 4,74 = –0,74; Vс.о./Vс.к. = 10–0,74 = 0,18.
Принимая Vс.о. = 20 – Vс.к., получим (20–Vс.к.)/Vс.к. = 0,18;
откуда объем раствора уксусной кислоты Vс.к. = 16,95 мл, и объем раствора ацетата натрия Vс.о. = 20 – 16,95 = 3,05 мл.
Задача 16. Удельная электрическая проводимость 0,175 М раствора аммиака равна 4,76´10–4 Ом–1см–1. Подвижность ионов NH4+ и ОН– при 25оС соответственно равны 73,5 и 198,3 Ом–1см2моль–1. Рассчитайте молярную проводимость, степень и константу ионизации аммиака, его рКb, концентрацию ионов водорода в растворе и его рН.
Решение: Удельная À и молярная l электрические проводимости связаны между собой соотношением
| À 1000 l = ¾¾¾¾¾, С
|
где С – концентрация в моль/л, 1000 – пересчетный коэффициент из литров в см3.
Рассчитываем l:
| 4,76´10–4·1000 l = ¾¾¾¾¾¾¾ = 2,72 Ом–1см2моль–1 0,175
|
Степень ионизации a можно вычислить с помощью отношения a=l/l¥, где l¥ – молярная проводимость при бесконечном разведении, которая рассчитывается по закону Кольрауша: l¥ = l+ + l– (l+ и l– – подвижности ионов):
l¥ = 73,5 + 198,3 = 271,8 Ом–1см2моль–1
Отсюда a = 2,72/271,8 = 0,01.
В соответствии с законом разведения Оствальда К = a2С/(1–a), где
К – константа ионизации электролита (в данном случае К = Кb
аммиака);
С – концентрация, выраженная в моль/л.
Находим Кb: Кb = 0,012·0,175/(1–0,01) = 1,77´10–5,
отсюда рКb = – lgКb = 4,752.
Концентрация ионов ОН– в растворе будет равна aС:
СОН– = 0,01·0,175 = 0,00175 моль/л.
Отсюда рОН = – lg0,00175 = 2,76 и, значит, pH = 14 – 2,76 = 11,24.
Задача 17. Написать формулу гальванического элемента, состоящего из медного электрода, погруженного в раствор сульфата меди с активностью 0,01 М и цинкового электрода, погруженного в раствор хлорида цинка с активностью 0,02 М.
Решение: Опорным при составлении формулы гальванического элемента является электрохимический ряд напряжений металлов, приведенный ниже:
Электрохимический ряд напряжений металлов
Li K Ba Ca Na Mg Al Mn Cr Zn Fe Co Sn Pb H2 Cu Hg Ag Au
Ослабление восстановительных свойств (активности) слева направо
Формула начинается со знака минус в круглых скобках, затем указывается металл, находящийся слева в ряду напряжений, в нулевой степени окисления. Ставится вертикальная черта, имеющая значение границы раздела между металлом и ионосодержащим раствором. За ней указывается активный ион. Далее следует вертикальная двойная черта, обозначающая границу между двумя полуэлементами и показывающая, чо диффузный потенциал устранен. За двойной чертой (в зеркальном порядке) указывается активный ион второго полуэлемента и, через одинарную вертикальную черту, металл в нулевой степени окисления, находящийся в электрохимическом ряду справа. За ним следует знак «плюс» в круглых скобках. Под каждым из активных ионов подписывается соответствующая ему активность из условия задачи. Конечный результат должен выглядеть следующим образом:
(-) Zn0 | Zn2+ || Cu2+ | Cu0 (+)
М 0,01М
Примечание: вместо активного иона позволительно указывать также и полную брутто формулу соли, в раствор которой погружен соответствующий электрод.
Задача 18. Рассчитайте электродные потенциалы, ЭДС гальванического элемента (–)Zn|ZnSO4 (c=0,5M)||CuSO4 (c=1M)|Cu(+), изменение энергии Гиббса DGо и константу равновесия реакции, протекающей в нем при замыкании цепи (Т=250С).
Решение: Потенциалы электродов вычислим с помощью уравнения Нернста:
| RT 0,059 ЕМеn+/Ме = ЕоМеn+/Ме + ¾¾ ln aМеn+ = EоМеn+/Ме + ¾¾¾ lg aМеn+, nF n
|
где ЕоМеn+/Ме – стандартный электродный потенциал (см. Приложение); aМеn+ – активность соответствующих ионов в растворе; n – число электронов, участвующих в электродной реакции; F – число Фарадея (96500 Кл).
Для расчета активности а = gС находим в справочнике коэффициенты активности g солей и подставляем их значения:
аCu2+ = 0,043´1=0,043 моль/л; аZn2+ = 0,063´0,5=0,0315 моль/л.
Отсюда
ЕCu2+/Cu= +0,337 + (0,059/2) lg 0,043 = +0,297 В;
ЕZn2+/Zn = –0,763 + (0,059/2) lg 0,0315 = –0,807 В.
И, значит, электродвижущая сила равна
Е = Е+ – Е– = +0,297–(–0,807) = 1,104 В.
Между DG0 реакции, протекающей в гальваническом элементе, и стандартной ЭДС существует связь, выражаемая уравнением: DGо = –nFEо.
Стандартная ЭДС рассчитывается как разность стандартных электродных потенциалов: Ео = Ео+ – Ео– . Значит
Ео = +0,337 –(–0,763) = 1,100 В,
и DGо = –2·96500·1,100 = –212300 Дж/моль.
Константа равновесия реакции (Ка = Кр) находится с помощью уравнения
DG0 = –RTlnKp,
откуда lnKа = lnKp = – DG0/RT = – (–212300)/[8,314·(25+273)] =
= 85,6887 и Ка = Кр = е85,6887 = 1,64´1037.
Задача 19. Рассчитать растворимость и произведение растворимости сульфида цинка при 25оС. Электродвижущая сила концентрационного гальванического элемента
| 1 2 Zn | ZnS || ZnSO4 | Zn а=х C=0,5М
|
равна 0,276 В.
Решение: ЭДС данного концентрационного элемента определяется уравнением:
| 0,059 aZn2+, (2) Е = ¾¾¾ lg ¾¾¾¾¾. n aZn2+, (1)
|
Примем, что aZn2+, (1) – концентрация (активность) ионов цинка в насыщенном растворе ZnS, равная х. Тогда aZn2+, (2) = gС= 0,063´0,5 = 0,0315 (см. предыдущую задачу).
Отсюда
| aZn2+, (2) n E 0,276·2 lg ¾¾¾¾ = ¾¾¾ = ¾¾¾¾ = 9,3559; x 0,059 0,059
aZn2+, (2) ¾¾¾¾ = 109,3559 = 2,2693´109; х |
и далее: х = aZn2+, (1) = 0,0315/(2,2693´109) = 1,391´10–11.
Значит, концентрация сульфида цинка в насыщенном растворе равна
1,39´10–11 моль/л, а его произведение растворимости -
ПР = СZn2+ · CS2– = х2 = (1,39´10–11)2 = 1,93´10–22.
Задача 20. Электродвижущая сила Е элемента, составленного из водородного и насыщенного каломельного электродов при 25°С равна 0,4185 В. Чему равны рН раствора, с которым контактирует водородный электрод, и активность ионов водорода в нем?
Решение:
| Е – ЕКЭ рН = ¾¾¾¾¾; 0,059 |
(потенциал каломельного электрода берем из Приложения). Отсюда
рН = (0,4185–0,2415)/0,059 = 3;
аН+ = 10–рН = 10–3 = 0,001 моль/л.
Задача 21. Константа скорости омыления этилацетата гидроксидом натрия при 10°С равна 2,38 мин–1. Определить время, необходимое для омыления 90% этилацетата, если реакционная смесь получены смешением 1л 0,05 н. раствора этилацетата с:
1)1 л 0,05 н. раствора NаОН; 2) 1 л 0,1 н. раствора NaОН.
Решение:
1) Реакция омыления этилацетата в щелочной среде является реакцией второго порядка. В случае равенства концентраций эфира и щелочи воспользуемся уравнением:
| 1 x 1 x k = ¾ · ¾¾¾, откуда t1 = ¾ · ¾¾¾, t1 a(a–x) k a(a–x) |
где а – исходное количество молей; х – количество прореагировавшего вещества к моменту времени t.
Общий объем смеси 2 л, поэтому концентрация веществ вследствие разбавления уменьшится в два раза и значит,
а = 0,025 моль/л, х = 0,025·0,9 = 0,0225 моль/л.
Отсюда
| 1 0,0225 t1 = ¾¾ · ¾¾¾¾¾¾¾¾¾¾ = 151,2 мин. 2,38 0,025(0,025–0,0225) |
2. Во втором случае концентрации эфира и щелочи неодинаковы, поэтому необходимо использовать уравнение:
| 1 b(a–x) k = ¾¾¾ ln ¾¾¾¾¾ t2(a–b) a(b–x) |
Если а - начальная концентрация этилацетата, а b – начальная концентрация щелочи, то а = 0,1/2 = 0,05 моль/л; b = 0,05/2 = 0,025 моль/л; x = 0,025´0,9 = 0,0225 моль/л.
Решаем уравнение относительно t2:
| 1 0,025(0,05–0,0225) t2 = ¾¾¾¾¾¾¾¾ ln ¾¾¾¾¾¾¾¾¾¾ = 28,65 мин 2,38 (0,05-0,025) 0,05(0,025–0,0225)
|
Задача 22. Константа скорости диссоциации фосгена
СОCl2 = CO + Cl2
при температуре 382оС равна 0,5´10–2 мин–1, а при температуре 482оС - 67,6´10–2 мин–1. Рассчитать: а) энергию активации реакции;
б) константу скорости реакции при температуре 425оС; в) количество фосгена, которое разложится при температуре 382оС за 100 минут после начала реакции, если начальное содержание его составляло 1 моль/л.
Решение:
а) Расчет энергии активации Е* ведем по уравнению:
| Т1Т2 R k2 Е* = ¾¾¾¾ ln ¾¾, T2–T1 k1 |
где: k1 и k2 – константы скорости реакции соответственно при
температурах Т1 и Т2. Подставляем значения:
655·755·8,314 67,6´10–2
Е*= ¾¾¾¾¾¾¾ln¾¾¾¾¾ = 201740,3 Дж/моль» 201,7 кДж/моль
755–655 0,5´10–2
б) Для расчета константы скорости реакции при 425оС воспользуемся тем же уравнением и найденным значением Е*.
| k3 Е* T3 – T1 ln ¾¾ = ¾ · ¾¾¾¾. k1 R T3T1 |
Решая это уравнение относительно k3, получим:
| 201740 698–655 ln k3 = ¾¾¾¾ · ¾¾¾¾¾ + ln 0,5´10–2 = –3,016, 8,314 698´655 |
откуда k3 = е–3,016 = 0,049.
в) Реакция диссоциации фосгена является реакцией первого порядка. Поэтому количество прореагировавшего фосгена может быть рассчитано по уравнению:
1 С0
k = ¾¾ ln ¾¾¾¾, где
t С0 - х
С0 – исходная концентрация вещества; C0–x – концентрация к моменту времени t; х – число молей прореагировавшего вещества.
Подставляя в это уравнение значение константы скорости реакции, время от начала реакции и исходную концентрацию, решаем уравнение относительно х:
0,5´10–2 = (1/100) ln [1/(1-х)];
ln [1/(1–x)] = 0,5; ln(1–x) = –0,5; 1–x = е-0,5 =0,6
и, окончательно, x = 0,4 моля.
Таким образом, при температуре 382оС за 100 минут от начала реакции концентрация фосгена уменьшится от 1 до 0,6 моль/л, так как в каждом литре разложится 0,4 моля фосгена.
Задача 23. Во сколько раз возрастет скорость разложения сульфацила натрия в глазных каплях при повышении температуры от 20 до 80оС? Температурный коэффициент скорости реакции равен 2.
Решение:
Воспользуемся соотношением vT2/vT1 = kT2/kT1= g (T2–T1)/10, где g=2, T2=80oС; T1=20оС:
Vt2/Vt1 = 26 = 64,
то есть скорость разложения возрастет в 64 раза.
Задача 24. Рассчитайте время разрушения аэрозольного препарата «Камфомен» на 10%, считая константу скорости разложения основного действующего вещества (фурацилина) равной 1,2´10–5 час–1 при 20oС.
Решение: Считая исходное количество вещества равным 100%, и используя кинетическое уравнение для реакции 1-го порядка
| 1 a k = ¾ ln ¾¾, t a–x |
получим:
| 1 100 0,1053 t = ¾ ln ¾¾¾¾ = ¾¾¾¾ = 8775 часов» 1 год. k 100–90 1,2´10–5 |
Задача 25. В течение какого времени через раствор сульфата меди необходимо пропускать ток силой 1,5 А, чтобы из него 6,4 г. меди?
Решение: По закону Фарадея масса выделившегося вещества при электролизе (в граммах) m = ЭJt/F, где
Э – электрохимический эквивалент вещества
J – сила тока (ампер)
t – время (Сек) Кулон
F – число Фарадея 96494 К/г-экв (¾¾¾) или 96500 К/г-экв.
г-экв
Электрохимическим эквивалентном называется количества вещества, выраженное в граммах, выделяемое 1к электричества, проходящим через электролит.
А
Э = ¾, где
n
А – атомная масса; n – валентность
Для меди 63,54
Э = ¾¾¾ = 31,77 г/к
2
mF 6,4 × 96500
t = ¾¾¾ = ¾¾¾¾¾¾ = 12959,8 сек = 216 мин = 3 ч. 36 мин.
ЭJ 31,77 × 1,5
Примеры решения задач по коллоидной химии
Задача 1. Найти поверхностное натяжение анилина s, если сталагмометрическим методом при 20oС получены следующие данные: число капель анилина n = 42, воды nо=18. Плотность анилина r=1,4´103 кг/м3; поверхностное натяжение воды sо=72,75´10–3 Н/м.
Решение: Используем для расчета формулу:
| nо r 18 · 1,4´103 s = sо ¾¾¾ = 72,75´10–3 ¾¾¾¾¾¾ = 43,65´10–3 Н/м. n rо 42 · 1´103 |
Задача 2. Найти поверхностное натяжение анилина, если методом наибольшего давления пузырьков получены данные: давление пузырьков при пропускании их через воду равно 11,8 × 102 Н/м, а в анилин – 712 Н/м.
Температура 200С, поверхностное натяжение воды s0 = 72,75 × 10-3 Н/м
Решение:
Используем для расчета формулу:
h р-ра 712
s = sН2О ¾¾¾ = 72,75´10–3 ¾¾¾¾¾¾ = 43,89´10–3 Н/м.
h Н2О 11,8´102
Задача 3. Используя константы уравнения Шишковского (a = 12,6´10-3 и b = 21,5), рассчитайте поверхностное натяжение водного раствора масляной кислоты с концентрацией 0,104 моль/л при 273К. Поверхностное натяжение воды при этой температуре s0 = 75,62´10-3 Н/м.
Решение: С помощью уравнения Шишковского
Ds = s0 - s = a ln(1 + bC)
рассчитаем поверхностное натяжение раствора s:
s = s0 - a ln(1 + bC) = 75,62´10-3 -12,6´10-3(1 + 21,5´0,104) =
=60,82´10-3 Н/м.
Задача 4. Коллоидный раствор колларгола содержит частицы серебра с диаметром 6´10–8 см. Определите число частиц, образующихся при диспергировании 0,5 см3 серебра, удельную поверхность золя и суммарную поверхность частиц, если они имеют: а) сферическую форму с диаметром (d) 6 × 10-8 см
б) кубическую с длиной ребра (ℓ) 10-6 см.
Решение: Зная радиус, можно рассчитать объем одной частицы (сферической)
Vч = 4/3pr3 = 4/3 [3,14 (3´10–8)3] = 113,04´10–24 см3
Vкуб. част. = ℓ3 = (10-6)3 = 10-18 см3
Теперь определим число частиц:
n = Vдисп. фазы/Vч = 0,5/113,04´10–24 = 4,4´1021 (сферических)
n = Vдисп. фазы/Vч = 0,5/10-18 = 0,5 × 1018 (кубических)
Удельную поверхность системы, содержащей сферические частицы, можно вычислить по формуле
| 3 3 Sуд= ¾ = ¾¾¾ =108 см–1; r 3´10–8 |
6 6
Sуд. куб. = ¾ = ¾¾¾ = 6 ×106 см–1
ℓ 10–6
Зная Sуд и суммарный объем частиц дисперсной фазы, найдем суммарную поверхность частиц:
Sсумм = SудVд.ф. = 108´0,5 =5´107 см2 (сферич.); Sкуб. = 6´106´0,5 = 3´106см2
Или иначе:
Sсумм= nSч = n4pr2 = 4,4´1021·4·3,14·(6´10-8)2 = 4,97´107» 5´107см2.
Задача 5. Определите поверхностный избыток (в кмоль/м2) при 10оС для водного раствора, содержащего 50 мг/л пеларгоновой кислоты С8Н17СООН. Поверхностные натяжения исследуемого раствора и воды соответственно равны 57´10–3 Н/м и 74,22´10–3 Н/м.
| Ds С Г= – ¾¾ · ¾¾. DС RT |
Решение: Используем уравнение Гиббса:
Выразим концентрацию раствора в кмоль/м3:
С = 0,05/158 = 3,164´10–4 моль/л = 3,164´10–4 кмоль/м3, (158 – молярная масса пеларгоновой кислоты). Отсюда
| (57´10–3 –74,22´10–3) 3,164´10–4 Г = - ¾¾¾¾¾¾¾¾¾¾ · ¾¾¾¾¾¾ = 7,32´10–9 кмоль/м2. 3,164´10–4 - 0 8,314´103´283 |
Задача 6. Определите длину молекулы масляной кислоты на поверхности раздела «раствор – воздух», если площадь, занимаемая одной молекулой в поверхностном слое, равна 30´10–20 м2, а плотность масляной кислоты r = 978 кг/м3.
Решение: Длина молекулы l рассчитывается по формуле
| Г¥ М l = ¾¾¾. r |
1
Учитывая, что S = ¾¾¾, (где NA-число Авогадро, равное
Г¥ NA
6,02´1026 молекул/кмоль), находим предельный поверхностный избыток:
1 1
Г¥ = ¾¾ = ¾¾¾¾¾¾¾¾¾ = 0,055´10–7 кмоль/м2.
S NA 30´10–20´6,02´1026
Тогда длина молекулы масляной кислоты (М=88):
| 0,055´10–7´88 l = ¾¾¾¾¾¾¾ = 4,95´10–10» 5´10–10 м = 5 Å (ангстрем). 978 |
Задача 7. При изучении адсорбции паров этанола на активированном угле были получены следующие данные:
| р´10–2, Па | 5,33 | 9,87 | 17,33 | 23,06 | 45,53 |
| А ´103, м3/кг | 14,9 | 19,1 | 24,2 | 27,3 | 36,8 |
(р - равновесное давление пара, А - величина адсорбции). Графически определите константы уравнений Фрейндлиха и Ленгмюра. Рассчитайте величину адсорбции при р = 3000 Па. Используя оба уравнения, вычислите, сколько этанола адсорбируется на 5 кг угля.
Решение: Для нахождения констант уравнения Фрейндлиха строят график зависимо






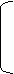

 KV1 n 0,0017·1000 4
KV1 n 0,0017·1000 4
 KV1 4 0,0017·1000 4
KV1 4 0,0017·1000 4
