Краткие теоретические сведения

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

ГОУ ВПО ЧЕРЕПОВЕЦКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

 

 

Факультет общих математических и естественнонаучных дисциплин

Кафедра химии

 

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

ПО  ДИСЦИПЛИНЕ

«ОБЩАЯ И НЕОРГАНИЧЕСКАЯ ХИМИЯ»

 

(Для студентов заочной формы обучения)

Часть 3

Учебно-методическое пособие

 

 

                                                       Специальности:    240301   Химическая технология

                                                        неорганических веществ;   280201 Охрана окру-

                                                           жающей  среды  и  рациональное  использование

                                                           природных ресурсов; 240801 Машины и аппара-

                             ты химических производств

 

 

Череповец

2007

 

 

Примеры решения задач по дисциплине «Общая и неорганическая химия» для студентов заочной формы обучения: В 3 ч. Ч. 3: Учеб.-метод. пособие. – Череповец: ГОУ ВПО ЧГУ, 2007. – 35 с.

 

 

Рассмотрено на заседании кафедры химии, протокол №  9 от 14.05. 07.

Одобрено редакционно-издательской комиссией факультета общих математических и естественнонаучных дисциплин ГОУ ВПО ЧГУ, протокол №  8 от 15.05. 07.

 

Составители:   О.А. Калько – канд. техн. наук, доцент;              

                      Ю.С. Кузнецова;

Н.В. Кунина

                          

 

Рецензенты:  С. Н. Балицкий  – канд. хим. наук, доцент (ГОУ ВПО ЧГУ);

                 Л.Ю. Кудрявцева – канд. техн. наук, доцент (ГОУ ВПО ЧГУ)

                      

 

 

Научный редактор: Г.А. Котенко – канд. хим. наук, профессор

 

 

                                                      © Калько О.А., Кунина Н.В.,

                                                           Кузнецова Ю.С., 2007

                                                      ©ГОУ ВПО Череповецкий государст-­

                                                                  венный  университет, 2007

 

ВВЕДЕНИЕ

Данное учебно-методическое пособие содержит краткие теоретические сведения и примеры решения задач по теме «Растворы» курса «Общая и неорганическая химия». Пособие предназначено для студентов заочной формы обучения в качестве вспомогательного руководства для самостоятельной работы при выполнении домашних контрольных работ. Содержание учеб­но-методического пособия соответствует государственному стандарту дисциплины «Общая и неорганическая химия» для химических специальностей.

 

 

РАСТВОРИМОСТЬ. СПОСОБЫ ВЫРАЖЕНИЯ

СОСТАВА РАСТВОРОВ

Краткие теоретические сведения

 

    Раствор – однофазная гомогенная система, состоящая из двух или более компонентов, а также продуктов их взаимодействия, состав которой может непрерывно меняться в пределах, ограниченных взаимной растворимостью веществ.

Вещество называют растворителем, если при образовании раствора оно не меняет своего агрегатного состояния, остальные компоненты раствора считают растворенными веществами. В случае, когда все компоненты при образовании раствора остаются в том же агрегатном состоянии, растворителем является компонент, которого в системе больше.

    Растворимостью называют, как способность вещества образовывать раствор с данным растворителем, так и количественную характеристику этой способности. Качественно растворимость характеризуется понятиями «хорошо растворимо», «мало растворимо», «нерастворимо». Количествен-ной мерой растворимости является масса вещества в граммах, которая способна раствориться в 100 г растворителя при данной температуре с образованием насыщенного раствора.

    Раствор называется насыщенным, если в нем находится предельное при данных условиях количество растворенного вещества. Если в растворе содержится больше растворенного вещества, чем это определяется растворимостью, раствор называется пересыщенным, а если меньше – ненасыщенным.

    Важнейшей характеристикой раствора является количественное содержание растворенных веществ. На практике состав раствора принято выражать с помощью следующих величин:

1. Массовая доля растворенного вещества w₂ (иначе процентная массовая концентрация) – отношение массы растворенного вещества m ₂ к массе раствора m

     (1)

Здесь и далее у величин, относящихся к растворителю, применяется индекс «1», индекс «2» относится к растворенному веществу, а отсутствие индекса указывает на свойство раствора как целого.

Это безразмерная величина, выраженная в долях единицы или в процентах, % масс. Таким образом, w₂ показывает, сколько грамм растворенного вещества содержится в ста массовых частях раствора.

2. Моляльная концентрация вещества С _m (иначе моляльность раствора) – отношение числа моль растворенного вещества n ₂ к массе растворителя m ₁ в килограммах

 ,                                              (2)

где М ₂ – молярная масса растворенного вещества, г/моль.

Если массу растворителя выражать в граммах, то для расчета моляльности следует пользоваться формулой

 .                                    (3)

Данный способ выражения состава раствора показывает, сколько моль растворенного вещества содержится в 1 кг растворителя. Его единицы измерения – моль/кг.

3. Молярная концентрация вещества С ₂ (иначе молярность раствора) – отношение числа моль растворенного вещества к объёму раствора V в дм³ (иначе в литрах)

 .                                           (4)

Она показывает, сколько моль растворенного вещества содержится в 1 дм³ раствора. Единицы измерения – моль/дм³ или М.

4. Молярная концентрация эквивалента вещества С ₂  (иначе нормальность раствора, нормальная концентрация или эквивалентная концентрация) – отношение числа моль эквивалентов растворенного вещества n ₂  к объёму раствора  в дм³

,                                 (5)

где М ₂ – молярная масса эквивалента растворенного вещества, г/моль; z – число эквивалентности растворенного вещества.

Нормальность раствора показывает, сколько моль эквивалентов растворенного вещества содержится в 1 дм³ раствора. Единицы измерения  –моль/дм³ или н.

Взаимосвязь между молярной и нормальной концентрациями одного и того же растворенного вещества выражается соотношением

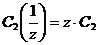.                                                (6)

То есть, эквивалентная концентрация в z раз больше молярной концентрации.

5. Титр раствора Т – масса растворенного вещества в граммах, которая содержится в одном см³ (иначе 1 мл) раствора

.                            (7)

Единицы измерения данного способа выражения состава раствора –г/мл или г/см³.

6. Мольная доля растворенного вещества х ₂ – отношение числа моль растворенного вещества к общему числу моль всех компонентов раствора n

.                          (8) 

Это безразмерная величина, выраженная в долях единицы.

 

Общее правило, используемое для приготовления разбавленных растворов из концентрированных: при одном и том же количестве растворенного вещества массы растворов и их массовые доли обратно пропорциональны друг другу:

w₁ × m ₁ = w₂ × m ₂,                                                  (9)

где m ₁(m ₂) – масса исходного (конечного) раствора. Если массу раствора представить через его плотность и объем, то формула (9) примет вид

ω₁ · ρ₁ · V ₁= ω₂ · ρ₂ · V ₂,                                      (10)

где V ₁(V ₂) – объем исходного (конечного) раствора; r₁ (r₂) – плотность исходного (конечного) раствора.

Если раствор получают путем смешивания двух растворов с различной концентрацией одного и того же растворенного вещества, то содержание растворенного вещества в конечном растворе можно определить с помощью правила смешивания: массы смешиваемых растворов m ₁ и m ₂ обратно пропорциональны разностям массовых долей w₁ и w₂  смешиваемых растворов и массовой доли смеси w₃

m ₁ / m ₂ = (w₃ – w₂) / (w₁ – w₃).                      (11)

При использовании правила смешивания применяют так называемое   правило креста (иначе квадрат Пирсона):

 

 

w₁                                      w₃ – w₂                       m ₁

               w₃

 w₂                                                     w₁ – w₃                              m ₂

          m ₁ / m ₂ = (w₃ – w₂) / (w₁ – w₃)

Пояснение: по диагонали из большей концентрации вычитают меньшую, получают   (w₁ – w₃), так какw₁ > w₃,  и (w₃ – w₂), так как w₃ > w₂. Затем составляют отношение масс исходных растворов m ₁ / m ₂.

Если при сливании двух растворов, содержащих различные по природе растворенные вещества, между ними происходит химическое взаимодействие, то по закону эквивалентов вещества реагируют в количествах, пропорциональных их эквивалентам. Например, для процесса взаимодействия кислоты с основанием будет выполняться соотношение

 .         (12)

 

Примеры решения задач

 

Пример 1. Растворимость KClO₃ при 20 °С равна 7,3 г/100 г воды, а при 100 °C – 56,2 г/100 г воды. Какая масса хлората калия выкристаллизуется из 50,0 г раствора данной соли насыщенного при 100 °C, если раствор охладить до 20 °C?

Р е ш е н и е

При охлаждении раствора масса воды, остается постоянной, а масса растворенного вещества, а значит, и масса раствора в целом, меняются. Из определения растворимости следует, что при 100 °C раствор содержит 100,0 г воды и 56,2 г KClO₃. Масса такого раствора составляет (100 + 56,2) = 156,2 г. По пропорции определяем массу воды в 50 г раствора

156, 2 г раствора — 100,0 г Н₂О;

50,0 г раствора — m ₁ г Н₂О;

Откуда m ₁ = 32,0 г Н₂О.

Тогда масса соли в 50,0 г горячего раствора равна: (50,0 – 32,0) = 18,0 г.

    По значению растворимости при 20 °C определяем, сколько соли будет растворено в 32 г воды

в 100 г Н₂О — 7,3 г KClO₃;

в 32,0 г Н₂О — х ₁ г KClO₃;

Откуда m ₂ = 2,3 г KClO₃.

Тогда масса KClO₃, выкристаллизовавшаяся после охлаждения раствора, равна (18,0 – 2,3) = 15,7 г.

 

Пример 2. Рассчитайте массовую долю и моляльную концентрацию глюкозы в растворе, полученном путем растворения 25 г глюкозы (С₆Н₁₂О₆) в 100 см³ воды.

Р е ш е н и е

Находим массу раствора, считая плотность воды равной 1 г/см³

.

Тогда по формуле (1) .

Для определения моляльной концентрации раствора найдем молярную массу глюкозы

М ₂(С₆Н₁₂О₆) = 12·6 + 1·12 + 6·16 = 180 г/моль.

Тогда по формуле (3)  .

Пример 3. В дистиллированной воде объёмом 250 мл растворили кристаллогидрат FeSO₄ ·7H₂О массой 50 г. Определите массовую долю кристаллогидрата и безводного сульфата железа (II) в растворе.

Р е ш е н и е

Найдем массу раствора, считая плотность воды равной 1 г/мл

.

Тогда по формуле (1) массовая доля кристаллогидрата FeSO₄ ·7H₂О

.

Определяем молярную массу безводного сульфата железа (II) и молярную массу кристаллогидрата

М ₂(FeSO₄) = 56 + 32 + 16·4= 152 г/моль;

М ₂(FeSO₄ ·7H₂О) = 152 + 7·18 = 278 г/моль.

Массу безводной соли в 50 г FeSO₄ ·7H₂О определяем по пропорции

 1 моль (278 г) FeSO₄ ·7H₂О содержит 1 моль (152 г) FeSO₄ ;

50 г FeSO₄ ·7H₂О содержит       m ₂ г FeSO₄ ;

Откуда           .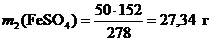

Массовая доля безводной соли FeSO₄ в 300 г раствора равна

 

Пример 4. Вычислите массовую долю (% масс.), молярную и молярную эквивалентную концентрации растворенного вещества, а также определите моляльность и титр раствора, полученного при растворении 18 г фосфата калия в 250 см³ воды, если плотность раствора r = 1,31 г/см³ = = 1310 г/дм³.

Р е ш е н и е

Находим массу раствора, считая плотность воды равной 1 г/см³

.

Тогда по формуле (1)    .

    Определяем молярную массу растворенного вещества

М ₂(К₃РO₄) = 3∙39 + 31 + 4∙16 = 212 г/моль.

Молярную концентрацию находим по формуле (4)

 .

    Для расчета молярной концентрации эквивалента вещества используем формулу (6)

,

где 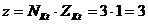; N _Kt – число катионов в 1 молекуле соли; Z _Kt – заряд катиона соли.

    Рассчитываем моляльную концентрацию раствора по формуле (3)

.

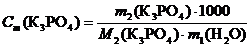
    Вычисляем титр раствора по формуле (7)

 .

Пример 5. Определите мольную долю сульфата алюминия в растворе с концентрацией 10 % масс.

Р е ш е н и е

Определяем молярные массы компонентов раствора

М ₂(Al₂(SO₄)₃) = 2∙27 + 3∙(32 + 16·4) = 342 г/моль;

М ₁(H₂О) = 18 г/моль.

По условию w₂(Al₂(SO₄)₃) = 10 % масс., значит в 100 г раствора содержится 10 г соли и 90 г воды. Тогда по формуле (8)

.

        

Пример 6. Рассчитайте массовый процент Al₂(SO₄)₃ в растворе с мольной долей соли х ₂ = 0,25.

Р е ш е н и е

Пусть общее количество раствора n = 1 моль, тогда мольная доля растворенного вещества будет равна числу моль данного компонента в растворе

.

Число моль растворителя определяем по формуле

.

Рассчитаем массы веществ, которые содержатся в 1 моль раствора

; .

Массовый процент Al₂(SO₄)₃ в растворе равен

 

Пример 7. Рассчитайте, какой объём 2,5 %-ного раствора КMnO₄ и воды нужно взять для приготовления 40 мл 0,05 %-ного раствора. Плотность 0,05 %-ного раствора равна 1,003 г/мл, а 2,5 %-ного – 1,017 г/мл.

Р е ш е н и е

Примем обозначения для величин, указанных в условии задачи:

Исходный раствор: w₁ = 2,5 % масс.; r₁ = 1,0175 г/мл; V ₁ –?;

Конечный раствор: w₂ = 0,05 % масс.; r₂ = 1,003 г/мл; V ₂ = 40 мл.

Приготовление раствора с концентрацией 0,05 % масс. из раствора с концентрацией 2,5 % масс. происходит путем разбавления последнего чистым растворителем, то есть водой, поэтому используем формулу (10). Из которой выражаем V ₁

Объем воды найдем по формуле, считая плотность воды r(Н₂О) = 1 г/мл

.

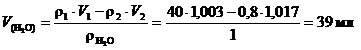       Пример 8. Сколько граммов 90 %-ного и 10 %-ного раствора серной кислоты необходимо взять для приготовления 800 г 40 %-ного раствора?

Р е ш е н и е

    Пользуясь правилом смешивания (иначе правилом креста), определяем соотношение весовых частей, в которых необходимо смешать 90 %-ный. и 10 %-ный растворы серной кислоты, чтобы получить 40 %-ный раствор по формуле (11)

m ₁ / m ₂ = (w₃ – w₂) / (w₁ – w₃) = (40 – 10) / (90 – 40) = 3/5.

    Таким образом, исходные растворы серной кислоты необходимо смешать в соотношении 3: 5.

По условию задачи необходимо получить 800 г 40 %-ного раствора серной кислоты. Поэтому 800 г делим на две части пропорциональные полученному отношению

 ; .

    Следовательно, необходимо взять 300 г 90 %-ного и 500 г 10 %-ного раствора серной кислоты.

 

Пример 9. Какой объем 0,52 М раствора гидроксида натрия потребуется для нейтрализации 15,45 см³ раствора серной кислоты с массовой долей 3 %  масс. и плотностью 1,018 г/см³.

Р е ш е н и е

Объем гидроксида натрия следует находить по закону эквивалентов. Для этого необходимо пересчитать концентрацию раствора серной кислоты из % масс. в нормальность.

Находим массу раствора кислоты, используя объем и плотность

.

Тогда из формулы (1) найдем массу серной кислоты

.

    Определяем молярную массу эквивалента серной кислоты

М ₂( Н₂SO₄) = .

По формуле (5) определяем нормальность раствора Н₂SO₄

 .

По формуле (6) определяем нормальность раствора гидроксида натрия

.

Объем NaOH найдем по формуле (12)

 .

 

Пример 10. Какое количество (см³) потребуется для приготовления 0,1 дм³ раствора серной кислоты с концентрацией 3,55 н из 96 %-ного Н₂SO₄ плотностью r = 1,836 г/см³.

Р е ш е н и е

    Массу Н₂SO₄, содержащуюся в растворе найдем из формулы (5)

 ;

 .

    Объем 96 %-ного раствора серной кислоты, необходимый для приготовления 0,1 дм³ 3,55 н раствора найдем из формулы (1)

.