МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ
БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Факультет прикладной математики и информатики
Кафедра теории вероятностей и математической статистики
Иванова Ивана Ивановича
Моделирование базовой случайной величины
Отчет по лабораторной работе №1
(«Имитационное и статистическое моделирование»)
Студента 4 курса 11 группы
| Работа сдана 13 октября 2018 г зачтена 2018 г (подпись преподавателя) | Преподаватель Гайдук Антон Николаевич |
Теоретическая часть
Моделирование БСВ
Линейный конгруэнтный метод
Согласно этому методу псевдослучайная последовательность реализаций 
БСВ 
определяется по рекуррентным формулам:
где 
, 
,..., 
– выходная последовательность генератора длины n, 
– начальное значение, a ≠ 0 – множитель, с – приращение, M – модуль.
Период датчика Т 
.
Метод Маклорена-Марсальи
Метод основан на комбинировании двух простейших программных датчиков БСВ (например, линейных конгруэнтных).
Пусть 
– псевдослучайные последовательности, порождаемые независимо работающими датчиками; 
– результирующая псевдослучайная последовательность реализаций БСВ; 
– вспомогательная таблица 
чисел.
Процесс вычисления включает следующие этапы:
· первоначальное заполнение таблицы 
:
· случайный выбор из таблицы:
· обновление табличных значений:
.
Данный метод позволяет ослабить зависимость между членами псевдослучайной последовательности и получить сколь угодно большие значения её периода Т при условии, что периоды Т1, Т2 исходных датчиков являются взаимно простыми числами.
Проверка точности моделирования
1.2.1 Тест «совпадения моментов»
Пусть в результате 
-кратного обращения к датчику БСВ получена выборка значений 
. Известно, что БСВ имеет среднее значение 
и дисперсию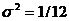 
. Обозначим случайные отклонения выборочных оценок от истинных характеристик 
как:
, 
(1.1)
где
, 
(1.2)
Тест «совпадения моментов» – это программа для ЭВМ, реализующая статистические критерии проверки по выборке А гипотез:
(1.3)
, 
(1.4)
Тогда решающее правило имеет вид:
принимается 
(1.5)
где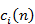 
– нормировочные множители; 
– порог критерия.
Если 
верна, а >>1 (практически ≥20), то в силу ЦПТ: 
~Ν1(0,1) (распределено приближённо по стандартному нормальному закону). С учётом этого из ограничения на вероятность ошибки первого рода:
(1.6)
находится выражение для порога критериев:
Δ = Ф-1(1 - 
), (1.7)
где Ф-1 
– квантиль стандартного нормального закона, 
– заданный уровень значимости.
В лабораторной работе реализована эквивалентная форма решающих правил, связывающей задаваемый пользователем уровень значимости 
и вычисляемые по выборке А критические вероятности 
-значения):
принимается 
, 
(1.8)
1.2.2 Тест «ковариация»
Ковариационной функцией случайной последовательности называется функция целочисленной переменной 
:
(1.9)
Если – независимые, одинаково распределённые по закону R(0,1) случайные величины, то 
и 
независимы для любого 
и следовательно:
(1.10)
Пусть 
– оценка 
по выборке , полученной в результате - кратного обращения к исследуемому датчику:
(1.11)
где 1<t<< 
– выборочное среднее. Заметим, что 
- выборочная дисперсия).
Тест «ковариация» позволяет проверить свойство (1.10) (гипотезу ) для последовательности 
и описывается следующим решающим правилом:
принимается 
(1.12)
где: 
для 
Δ – порог, определённый для заданного уровня значимости по формуле:
Δ = Ф-1(1 - ). (1.13)
В лабораторной работе использована эквивалентная форма правила (1.12):
принимается 
, 
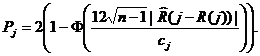(1.14)
