1. На рисунке 1 АЕ – биссектриса треугольника АВС, АD = DЕ, АЕ = СЕ, 
АСВ = 37°. Найдите ВDЕ.
2. На рисунке 2 АD – биссектриса треугольника АВС, АО = ОD, МО 
АD. Докажите, что МD || АВ.
Рис. 1 Рис. 2
3. Решить задачи №№ 217, 211 (б).
III. Самостоятельная работа (проверочного характера с анализом ее выполнения).
Вариант I
1. На рисунке 12 прямые а и b параллельны, угол 2 на 34° больше угла 1. Найдите угол 3.
2. Через вершину прямого угла С треугольника АВС проведена прямая СD, параллельная стороне АВ. Найдите углы А и В треугольника, если DСВ = 37°.
Вариант II
1. На рисунке 13 прямые а и b параллельны, угол 2 в четыре раза меньше угла 1. Найдите угол 3.
2. Через вершину С треугольника СDЕ с прямым углом D проведена прямая СР, параллельная прямой DЕ. Найдите углы С и Е треугольника, если РСЕ = 49°.
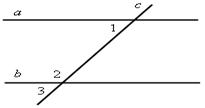
Рис. 3 Рис. 4
IV. Итог урока.
Домашнее задание: подготовиться к контрольной работе, решить № 210.
Урок 41
КОНТРОЛЬНАЯ РАБОТА № 3 «ПАРАЛЛЕЛЬНЫЕ ПРЯМЫЕ»
Цели: проверить знания, умения и навыки учащихся по теме «Параллельные прямые» и применение знаний к решению задач.
Ход урока
I. Организация учащихся на выполнение работы.
II. Выполнение работы по вариантам.
Вариант I
1. Отрезки ЕF и РD пересекаются в их середине М. Докажите, что РЕ || DF.
2. Отрезок DМ – биссектриса треугольника СDЕ. Через точку М проведена прямая, параллельная стороне СD и пересекающая сторону DЕ в точке N. Найдите углы треугольника DМN, если СDЕ = 68°.
Вариант II
1. Отрезки MN и EF пересекаются в их середине P. Докажите, что ЕN || MF.
2. Отрезок АD – биссектриса треугольника АВС. Через точку D проведена прямая, параллельная стороне АВ и пересекающая сторону АС в точке F. Найдите углы треугольника АDF, если ВАС = 72°.
Вариант III
(для более подготовленных учащихся)
1. Отрезок АD – биссектриса треугольника АВС. Через точку D проведена прямая, пересекающая сторону АВ в точке Е так, что АЕ = ЕD. Найдите углы треугольника АЕD, если ВАС = 64°.
2. На рисунке 14 АС || ВD, точка М – середина отрезка АВ. Докажите, что М – середина отрезка СD.
Вариант IV
(для более подготовленных учащихся)
1. Отрезок DM – биссектриса треугольника СDЕ. Через точку М проведена прямая, пересекающая сторону DЕ в точке N так, что DN = MN. Найдите углы треугольника DMN, если СDЕ = 74°.
2. На рисунке 15 АВ || DС, АВ = DС. Докажите, что точка О – середина отрезков АС и ВD.
III. Итоги урока.
Домашнее задание: повторить пункты 5–29.
Вариант I
1. Отрезки ЕF и РD пересекаются в их середине М. Докажите, что РЕ || DF.
2. Отрезок DМ – биссектриса треугольника СDЕ. Через точку М проведена прямая, параллельная стороне СD и пересекающая сторону DЕ в точке N. Найдите углы треугольника DМN, если СDЕ = 68°.
Вариант II
1. Отрезки MN и EF пересекаются в их середине P. Докажите, что ЕN || MF.
2. Отрезок АD – биссектриса треугольника АВС. Через точку D проведена прямая, параллельная стороне АВ и пересекающая сторону АС в точке F. Найдите углы треугольника АDF, если ВАС = 72°.
Вариант I
1. Отрезки ЕF и РD пересекаются в их середине М. Докажите, что РЕ || DF.
2. Отрезок DМ – биссектриса треугольника СDЕ. Через точку М проведена прямая, параллельная стороне СD и пересекающая сторону DЕ в точке N. Найдите углы треугольника DМN, если СDЕ = 68°.
Вариант II
1. Отрезки MN и EF пересекаются в их середине P. Докажите, что ЕN || MF.
2. Отрезок АD – биссектриса треугольника АВС. Через точку D проведена прямая, параллельная стороне АВ и пересекающая сторону АС в точке F. Найдите углы треугольника АDF, если ВАС = 72°.
Вариант I
1. Отрезки ЕF и РD пересекаются в их середине М. Докажите, что РЕ || DF.
2. Отрезок DМ – биссектриса треугольника СDЕ. Через точку М проведена прямая, параллельная стороне СD и пересекающая сторону DЕ в точке N. Найдите углы треугольника DМN, если СDЕ = 68°.
Вариант II
1. Отрезки MN и EF пересекаются в их середине P. Докажите, что ЕN || MF.
2. Отрезок АD – биссектриса треугольника АВС. Через точку D проведена прямая, параллельная стороне АВ и пересекающая сторону АС в точке F. Найдите углы треугольника АDF, если ВАС = 72°.
Вариант I
1. Отрезки ЕF и РD пересекаются в их середине М. Докажите, что РЕ || DF.
2. Отрезок DМ – биссектриса треугольника СDЕ. Через точку М проведена прямая, параллельная стороне СD и пересекающая сторону DЕ в точке N. Найдите углы треугольника DМN, если СDЕ = 68°.
Вариант II
1. Отрезки MN и EF пересекаются в их середине P. Докажите, что ЕN || MF.
2. Отрезок АD – биссектриса треугольника АВС. Через точку D проведена прямая, параллельная стороне АВ и пересекающая сторону АС в точке F. Найдите углы треугольника АDF, если ВАС = 72°.
Вариант I
1. Отрезки ЕF и РD пересекаются в их середине М. Докажите, что РЕ || DF.
2. Отрезок DМ – биссектриса треугольника СDЕ. Через точку М проведена прямая, параллельная стороне СD и пересекающая сторону DЕ в точке N. Найдите углы треугольника DМN, если СDЕ = 68°.
Вариант II
1. Отрезки MN и EF пересекаются в их середине P. Докажите, что ЕN || MF.
2. Отрезок АD – биссектриса треугольника АВС. Через точку D проведена прямая, параллельная стороне АВ и пересекающая сторону АС в точке F. Найдите углы треугольника АDF, если ВАС = 72°.
Вариант I
1. Отрезки ЕF и РD пересекаются в их середине М. Докажите, что РЕ || DF.
2. Отрезок DМ – биссектриса треугольника СDЕ. Через точку М проведена прямая, параллельная стороне СD и пересекающая сторону DЕ в точке N. Найдите углы треугольника DМN, если СDЕ = 68°.
Вариант II
1. Отрезки MN и EF пересекаются в их середине P. Докажите, что ЕN || MF.
2. Отрезок АD – биссектриса треугольника АВС. Через точку D проведена прямая, параллельная стороне АВ и пересекающая сторону АС в точке F. Найдите углы треугольника АDF, если ВАС = 72°.
Урок 31
СУММА УГЛОВ ТРЕУГОЛЬНИКА
Цели: доказать теорему о сумме углов треугольника, следствия из нее; ввести понятия остроугольного, прямоугольного и тупоугольного треугольников; рассмотреть задачи на применение доказанных утверждений.
Ход урока
