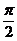Связь между декартовой и полярной системами координат.

Глава 5. Полярная система координат

Полярная система координат на плоскости.

 

 

Полярные координаты.

 

Положение точки на плоскости может быть задано не только декартовыми прямоугольными координатами, но и другими способами.

Довольно часто применяется так называемая полярная система координат. Полярная система координат определяется заданием точки О, которая называется полюсом, луча ОА, который выходит из этой точки и называется полярной осью, а также масштаба для измерения длин.

Пусть М - произвольная точка плоскости (рис. 1). Обозначим через r расстояние от точки М до полюса O (r =ú O M ê) и через j - угол, который будем отсчитывать от полярной оси против часовой стрелки (j = =Ð A O M).

 

 

j

r,,,,

M

                        

 

		r

 

j

                       

                   O

											A

 

                                      Рис. 1        

 

Числа r и j называются полярными координатами точки М относительно заданной системы: r - полярный радиус (первая координата); j - полярный угол (вторая координата).

По определению величина r положительная. Задание полярного радиуса и полярного угла определяет положение точки на плоскости единственным образом.

Если же надо указать полярные координаты какой-нибудь точки на плоскости, то ей будет соответствовать единственное значение полярного радиуса r и бесконечное множество значений полярного угла, т. е. полярный угол определяется неоднозначно: , где  (  Z).

Среди возможных значений полярного угла точки М выделяют одно определенное значение угла , которое удовлетворяет неравенствам:  (или ). Ограничение изменения угла дает возможность на практике для каждой точки плоскости указать также однозначно ее полярные координаты. Можно сказать, что в качестве главного значения полярного угла берется угол, на котором нужно повернуть луч ОА до совмещения с лучом ОМ, но делая при этом поворот не более чем на 180⁰ в ту или другую сторону. Исключение составляет только полюс О, для которого r = 0, а угол не имеет определенного значения.

 

П р и м е р. Построить точки, заданные полярными координатами:

, , , .

 

Порядок построения: на плоскости указать точку О (полюс) и луч ОА, который выходит из точки О (полярная ось); указать единицу длины. После этого от луча ОА, отложить заданный угол и построить луч ОМ, на котором, используя масштаб, указать точку так, чтобы длина отрезка соответствовала первой координате точки.

Построение точек показано на рис. 2.

     

              

M

 

1

O

B

E (2; 0)

                                      Рис. 2

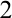
Упражнение. Построить точки, заданные полярными координатами:

, , , .

 

 

Связь между декартовой и полярной системами координат.

 

В некоторых случаях приходится одновременно пользоваться и декартовой, и полярной системами координат.

Если начало декартовой прямоугольной системы координат совместить с полюсом, а ось Ох направить по полярной оси, то прямоугольные координаты x и y точки М и ее полярные координаты r и j связаны следующими формулами (рис. 3):

 

                   ,                                             (1)

                   .                                               (2)

 

 

 

                                 Рис. 3

 

Из этих формул следует, что

 

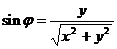                       ,                            (3)

Формула  определяет два угла j и (j + p) в пределах одной окружности. Формулы (3) уточняют, какой из этих углов необходимо выбрать. Эти соотношения позволяют находить декартовы координаты точки по заданным полярным, а также решать обратную задачу.

 

П р и м е р 1. Найти декартовы координаты точек, если полюс совпадает с началом координат, а полярная ось направлена по оси абсцисс: , , .

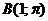Решение. Подставляя полярные координаты точек в формулы (1), найдем их декартовы координаты:

а) для точки :

          ;

 

б) для точки :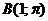

 

          ;

 

в) для точки :

          .

 

Примечание.

 

                                 По формулам приведения имеем:

(II четверть)

(II четверть)

 или                 

 или   

 

П р и м е р 2. Найти полярные координаты точек, если полюс совпадает с началом координат, а полярная ось - с положительным направлением оси абсцисс:

 

, , .

 

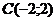Решение. По формулам (2) имеем:

 

а) для точки :

(I четверть)

              

 

 

         

 

 

б) для точки :

	(IV четверть)

 

 

         

 

или

 

в) для точки :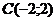

	(II четверть)

 

 

находится во II

четверти (рис. 4.)

Так как

 

 

                        

 

		II

 

 

                                      Рис. 4

 

Ответ: .

 

 

Упражнения

 

1. Построить точки, заданные полярными координатами:  Найти декартовые координаты этих точек.

Ответы: .

 

2. Найти полярные координаты точек:

 

.

 

Ответы: .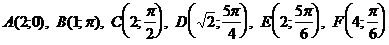

3. Найти полярные координаты точек, симметричных относительно полярной оси точкам:

.

Ответы: .

 

 

Полярные уравнения линий.

 

Важнейшим понятием геометрии является понятие уравнения линии.

Уравнением данной линии (в выбранной системе координат) называется такое уравнение F (x, y)=0 с двумя переменными, которому удовлетворяют координаты x и y каждой точки, лежащей на этой линии, и не удовлетворяют координаты никакой точки, не лежащей на ней.

Линия, определенная данным уравнением (в некоторой системе координат), есть геометрическое место всех точек плоскости, координаты которых удовлетворяют этому уравнению.

Так как величины x и y рассматриваются как координаты переменной точки, то их называют текущими координатами.

Текущие координаты следует обозначать другими буквами, если используется другая, не декартова система координат.

Так, в полярной системе координат линия задается уравнением F (r; j) = 0,связывающим полярные координаты ее текущей точки. Если возможно, то уравнение разрешают относительно r. Тогда полярное уравнение принимает вид:   r = r (j).

Если функция r (j) непериодическая, то углу j придают все возможные для данной функции значения, не ограничиваясь изменением его только в пределах первого периода.

Чтобы перейти от уравнения линии F (x, y)=0 в декартовых координатах к ее полярному уравнению, необходимо подставить в декартово уравнение вместо х и у их выражения из формулы (1).

Обратный переход от полярного уравнения F (r; j)= 0 к декартову уравнению той же линии осуществляется с помощью формул (2) и (3).

 

 

П р и м е р 1. Найти полярное уравнение прямой х = 1.

 

Решение. Обратим внимание, что прямая проходит через I и IV четверти (рис. 5). Известно, что х= r × cos j [формула (1)], тогда полярные координаты связаны следующим условием для данной прямой:

 

                              .

 

Это и есть уравнение данной прямой в полярной системе координат.

                            

 

 

 

                                  Рис. 5

 

Так как r - величина положительная, то дробь  также положительна, а это означает, что , т.е. угол j  может меняться в пределах I и IV четвертей, а значит данная прямая проходит через I и IV четверти.

 

 

П р и м е р 2. Найти полярное уравнение прямой, не проходящей через начало координат.

 

Решение. Из аналитической геометрии известно нормальное уравнение прямой: , где р - расстояние от начала координат до прямой, a - полярный угол нормали ОВ (ОВ ^ l) (рис. 6).

 

                                                        

 

 

 

                                  Рис. 6

 

Заменяя х и у на r и j по формулам (1), получим:  или .

По условию прямая не проходит через начало координат, поэтому ее расстояние p от начала координат отлично от 0. Тогда из последнего равенства следует, что при любом j  и .

Полярное уравнение данной прямой - .

 

П р и м е р 3. Дано полярное уравнение линии:  (лемниската       Бернулли). Найти ее уравнение в декартовой системе координат.

 

Решение. Воспользуемся формулой тригонометрии для синуса двойного      аргумента 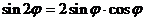 и подставим в уравнение линии:

 

      .

 

                   .

Тогда  или  - уравнение данной линии в      декартовой системе координат.

 

П р и м е р 4. Что представляют собой линии, заданные в полярной системе     координат:  (I)  и  (II).

 

Решение.

I. Геометрическое место точек, для которых r - расстояние до полюса постоянно, есть окружность. Уравнение  определяет окружность радиуса  с центром в полюсе О.

 

II. Уравнению  удовлетворяют все точки полупрямой (луча), проведенной из полюса под углом a  к полярной оси. При этом вся прямая, проходящая через полюс, записывается в полярной системе координат уравнениями:  и .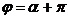

 

П р и м е р 5. Какую линию определяет уравнение , где >0,              переменные r и j - полярные координаты?

 

Решение. Обозначим через М точку с полярными координатами 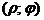 и        через А - точку с полярными координатами (; 0). Если , то Ð ОМА - прямой, и обратно (рис. 7).

 

                  

 

 

 

                                          

 

                             Рис. 7

 

Следовательно, геометрическое место точек, полярные координаты которых удовлетворяют уравнению , представляет собой окружность с диаметром ОА.

 

П р и м е р 6. Какую линию определяет полярное уравнение ?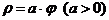

 

Решение. Так как r и  - положительные величины, угол j может изменяться только в положительную сторону. При  также и 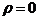, т.е. данная линия выходит из полюса. При возрастании угла j от О также пропорционально возрастает и r.

Следовательно, текущая точка  данной линии, исходя из полюса, движется вокруг него, одновременно удаляясь от полюса. В результате точка М описывает спираль, называемую спиралью Архимеда (рис. 8).

 

2 π a

 

 

                                            Рис. 8

 

 

За один оборот точка  перейдет в новое положение , где , а . Поэтому расстояние между точками М и  есть величина постоянная. Таким образом, спираль Архимеда рассекает каждый полярный луч на равные отрезки длины 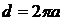, не считая отрезка, примыкающего к полюсу.

П р и м е р 7. Дано уравнение лемнискаты в декартовой системе координат: . Составить полярное уравнение лемнискаты и построить кривую.

 

Решение. Переходим к полярным координатам с помощью формул  и .

Тогда получим:

     

или  - уравнение лемнискаты в полярных координатах.

 

Для построения кривой находим из этого уравнения . Из того, что в правой части равенства стоит двойной знак (), а также из того, что уравнение не меняется при замене j на (- j), заключаем, что лемниската расположена симметрично относительно осей Ох и Оу. Исследуем форму лемнискаты для I четверти, т.е. для случая , . Для этих значений r и j имеем: 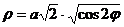. Очевидно, что j может изменяться только в промежутке от 0 до . Таким образом, соответствующая часть кривой заключена между полярной осью и лучом . Если , то . С возрастанием j от 0 до      величина r убывает до значения r = 0. Учитывая симметрию, можно построить лемнискату (рис. 9).

 

   

 

 

Рис. 9

П р и м е р 8. Дано полярное уравнение линии . Построить эту     линию по точкам, задавая углу j значения через промежуток  (шаг). Найти ее декартово уравнение, расположив декартову систему координат так, как       показано на рис. 3.

 

Решение. Поскольку левая часть данного уравнения неотрицательна, то угол j может изменяться только в тех пределах, для которых , т.е.  (I четверть) и  (III четверть). На рис. 10 представлен график функции  и заштрихованы области, соответствующие значениям аргумента, принадлежащих I и III четвертям. При изменении аргумента от 0 до 2 p значение функции неотрицательно только для  и .

                              

 

 

                             Рис. 10

 

     

Результаты вычисления значений r (с точностью до 0,01) внесем в таблицу. Пусть значение аргумента j  изменяется от 0 до 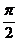 с шагом .

 

 

                                                                                           Таблица

 

№ точек	j	2 j
1	0	0	0	0
2			0,50	2,12
3			0,87	2,79
4			1	3
5			0,87	2,79
6			0,50	2,12
7		p	0	0

 

Для построения линии проводим из полюса лучи, соответствующие выбранным значениям j, и на каждом луче откладываем вычисленные значения        полярного радиуса. Полученные точки соединяем плавной кривой (рис. 11).

При изменении угла j в пределах III четверти  будет принимать те же значения, что и в I четверти, т.е. линия будет расположена симметрично относительно начала координат.

 

Построенная линия носит название лемнискаты Бернулли.

Найдем уравнение этой линии в декартовой системе координат.

           .

   Из формул (2) и (3):

                             .

 

Þ   Þ

 

- уравнение линии в декартовой системе координат.

M6

M5

M4

M3

M2

(I)

1

O

Y

 

X

0

(III)

                                Рис.11  

 

 

Очевидно, что строить данную линию проще, используя полярную систему координат.

 

 

Упражнения

1. В полярной системе координат составить уравнение окружности с центром в полюсе.

      Ответ: .

 

2. Найти полярное уравнение прямой  (см. пример 2).

      Ответ: .

3. Найти полярное уравнение окружности .

        Ответ: .

4. Построить по точкам, задавая углу j значения через промежуток , кардиоиду  ( >0). Написать декартово уравнение кардиоиды.

      Ответ:

5. На спирали Архимеда  взята точка С, полярный радиус которой равен 47. Определить, на сколько частей эта спираль рассекает полярный радиус точки C. Сделать чертеж.

 

      Ответ: на пять частей.