CP / CV ВОЗДУХА МЕТОДОМ АДИАБАТИЧЕСКОГО РАСШИРЕНИЯ»
(лабораторная работа № 24)
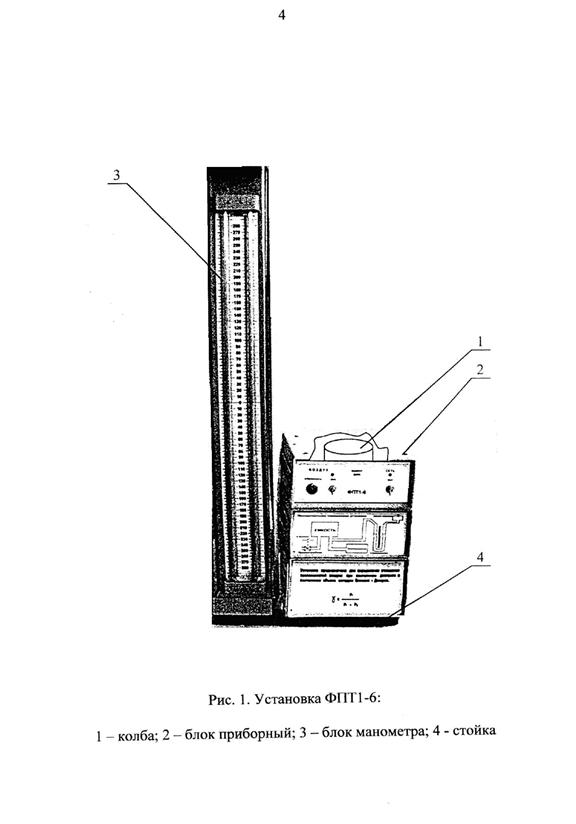
Приборы и принадлежности: лабораторная установка ФПТ1 – 6.
Цель работы: экспериментальное определение показателя адиабаты для воздуха.
Краткая теория
Молярной теплоёмкостью вещества называется физическая величина С, численно равная количеству тепла, которое нужно сообщить одному молю вещества для повышения его температуры на 1К в некотором термодинамическом процессе.
Молярная теплоёмкость
(ν – число молей газа).
Для данного вещества величина С зависит от условий, при которых происходит передача тепла. Так, для газов молярная теплоёмкость Cp при изобарном процессе (p = const) отличается от молярной теплоёмкости Cv при изохорном процессе (V=const). Действительно, по первому началу термодинамики (dQ = dU + dA) для элементарного изохорного процесса dQ = dU, где U – внутренняя энергия одного моля газа и тогда 
= 
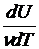(dU = ν CvdT). В то же время для элементарного изобарного процесса
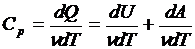
(dA = pdV - элементарная работа, совершенная газом при расширении).
В результате CP = CV + 
, т.е. Cp > Cv. Физический смысл этого можно пояснить следующим примером. Пусть газ заключен в цилиндр с подвижным поршнем. Если поршень закреплен, то для повышения температуры газа на dT ему нужно сообщить количество тепла dQ = νС v dT. Если же поршень свободен, то газ при нагревании расширяется, передвигая поршень, и совершает тем самым работу против внешних сил. Для этого требуется дополнительное количество тепла, так что dQp > dQv и Cp > Cv.
Так как dU =ν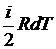 
, а с другой стороны, dU =ν CvdT, то 
(i – число степеней свободы молекулы данного газа). Согласно уравнению Майера Cp = Cv + R. Тогда 
.
|
|
2→3 воздуха, оставшегося в колбе). Когда температура воздуха Т3 в сосуде сравняется с первоначальной Т1 (температурой окружающего воздуха), то давление воздуха в колбе станет равным p 3. При адиабатическом расширении воздуха 1→2, согласно уравнению Пуассона:
p1V1γ = p2V2γ, (1)
где V 1 – первоначальный объем воздуха, который при расширении займет объем V к колбы. С другой стороны,
p 1 V 1 = p 3 V 3. (2)
так как в соотношении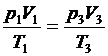 
температура T 1 равна температуре T 3..
Поскольку V2= V3= Vк, то из (1) и (2) получаем:
.
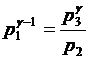Отсюда (γ – 1)lg p 1 = γlg p 3 - lg p 2 и тогда: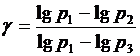 
.
Так как в условиях опыта давления p 1 и p 3 мало отличаются от p 2 (p а), то с достаточной точностью можно записать
.
Так как второе колено манометра открыто, то p 1 = p м1 + p 2, p 3 = p м2 + p 2 , где p м1 и p м2 – показания манометра (в кПа) для установившихся состояний 1 и 3 соответственно. Тогда
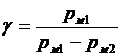. (3)
Порядок выполнения работы
1. По разрешению преподавателя тумблером в модуле «СЕТЬ» подайте на установку напряжение 220 В. При этом на панели модуля загорится сигнальная лампа (светодиод).
2. Включите подачу воздуха в колбу, установив тумблер в модуле «ВОЗДУХ» в положение «ВКЛ.». При этом загорится светодиод, и начнет работать микрокомпрессор. Внимательно следите за подъемом уровня воды в левом колене манометра, который во всех случаях не должен превышать 200 дел. по шкале манометра. После достижения рабочего давления в 3,0 – 3,5 кПа выключите тумблер в модуле «ВОЗДУХ».
3. Через 5 – 10 с произведите отсчет давления p м1 по манометру (по разности уровней воды в его коленах). Занесите это значение давления p м1 в таблицу.
4. Немного поверните ручку пневмоклапана «АТМОСФЕРА» по часовой стрелке, и как только показания манометра установятся на нуле, верните ручку пневмоклапана в исходное положение.
5. Следите за подъемом давления в колбе, и как только положения уровня воды в трубках перестанут изменяться, запишите в таблицу величину давления p м2.
6. Все действия и измерения повторите еще 4 раза. Рассчитайте величины γ1,…, γ5 по формуле (3) и найдите <γ>.
7. Рассчитайте абсолютную погрешность Δγ, приняв ее равной стандартной погрешности:
.
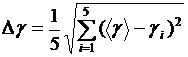Найдите относительную погрешность измерений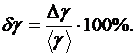 
| № опыта | рм1, кПа | рм2, кПа | γ | <γ> | Δγ | Δγ, % |
| 1 |
|
|
| |||
| 2 | ||||||
| 3 | ||||||
| 4 | ||||||
| 5 |
8. Запишите окончательный результат работы в виде γ = <γ>±Δγ с δγ = ….%.
Контрольные вопросы
1. Какой газ можно считать идеальным?
2. Какие изопроцессы, происходящие в идеальном газе, Вы знаете? Запишите их уравнения.
3. Как связаны теплоемкости Cv и Cp идеального газа с числом степеней свободы его молекул?
4. На основании измеренного значения γ для воздуха сделайте заключение о строении молекул основных газов в его составе.
