Основной закон динамики вращательного движения твердого тела:
, где
- момент количества движения твердого тела,
- момент внешних сил, действующих на тело.
Для однородного тела, вращающегося относительно оси симметрии этого тела,
, где
- угловая скорость. Вектор направлен по оси вращения в соответствии с правилом правого винта.
В этом случае
, или 
Отсюда 
, где
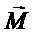- момент внешней силы 
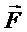относительно данной оси вращения, то есть проекция вектора момента внешней силы 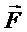на данную ось вращения (направление вектора коллинеарно оси вращения);
- угловое ускорение (направление вектора коллинеарно оси вращения и совпадает с направлением вектора ).
Таким образом, в рассматриваемом случае основной закон динамики вращательного движения твердого тела относительно неподвижной оси:
Если на тело, имеющее ось вращения (совпадающую с осью симметрии данного тела), действует сила, то это тело приобретает угловое ускорение , величина которого прямо пропорциональна моменту действующей силы относительно данной оси вращения и обратно пропорциональна моменту инерции этого тела относительно той же оси вращения.
Согласно этому закону для какого-либо тела с неизменным моментом инерции относительно выбранной оси вращения (оси симметрии данного тела) величина углового ускорения линейно зависит от величины момента действующей силы относительно данной оси вращения, то есть 
. Линейная зависимость углового ускорения 
от величины 
может быть проверена экспериментально с помощью «прибора Обербека».
|
|
Рис. 1. Принципиальная схема «прибора Обербека»
Прибор Обербека состоит их металлического «креста», способного вращаться вокруг неподвижной оси под действием силы натяжения Т разматывающейся нити, на которой подвешен груз массой m.
Используя набор грузов с разными массами m1, m2, m3 …, с помощью прибора Обербека можно определить в результате косвенных измерений моменты сил натяжения нити: 
и соответствующие им величины углового ускорения 
По точкам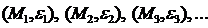 
можно построить экспериментальную графическую зависимость 
и проверить ее соответствие линейной зависимости.
Момент силы натяжения нити Т можно получить из второго закона Ньютона для поступательного движения груза m:
, где
a – ускорение, с которым движется груз,
F – сила, вызывающая это ускорение. 
Отсюда 
, а момент этой силы относительно оси вращения 
, где r - плечо силы Т (радиус шкива).
Так как угловое ускорение 
, то экспериментальная часть данной работы состоит в определении радиуса шкива r и линейного ускорения движения груза m. Радиус шкива r определяется с помощью штангенциркуля. Все ускорения a можно определить опытным путем с использованием формулы 
, получаемой из 
, где
h – путь, пройденный грузом за время t после начала движения с ускорением a.
Таким образом, для определения величины ускорения a необходимо провести измерения пути h и времени t движения груза m.
Порядок выполнения работы
1. Подготовим таблицы для результатов измерений
Таблица 1
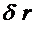
 , м
|  , м
| 
|  , м
|  , м
| 
|
Таблица 2
| N | m | m, кг | t1 , c | t2 , c | t3 , c | t4 , c | t5 , c | t ср , c | D t, c | d t |
| 1 | m 1 | 0,1 | ||||||||
| 2 | m 2 | 0,2 | ||||||||
| 3 | m 3 | 0,3 | ||||||||
| 4 | m 4 | 0,4 |
Таблица 3
| N | m | a, м/с2 | M, Н×м | d M | D M, Н×м | e, рад/с2 | d e | D e, рад/с2 |
| 1 | m 1 | |||||||
| 2 | m 2 | |||||||
| 3 | m 3 | |||||||
| 4 | m 4 |
2. Установим все четыре груза Е (рис.1) в крайнем, дальнем от оси вращения положении и закрепим их винтами.
3. Измерим диаметр шкива и определим радиус шкива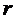 
. Занесем его значение в табл. 1.
4. Намотаем нить на шкив и к свободному концу нити подвесим груз m. Измерим расстояние от верхнего положения груза m по пола. (Для проведения измерений и расчетов удобно, чтобы груз m в каждом опыте проходил одно и то же расстояние h от верхнего, выбираемого нами уровня, до нижнего уровня - пола.)
5. Рассчитаем абсолютную и относительную погрешности определения радиуса шкива r и высоты h. Абсолютные погрешности 
и 
принимаем равными половине цены наименьшего деления измерительного инструмента (штангенциркуля и линейки соответственно), относительную погрешности определяем по формулам: 
, 
.
6. Используя последовательно грузы m = m1, m2, m3, m4, определим время их прохождения пути h. Время движения груза m измерим с помощью секундомера, причем для уменьшения погрешности измерения времени для каждого груза m = m1, m2, m3, m4 проведем по пять опытов и измерений t 1, t 2, t 3, t 4, t 5. Для каждого груза найдем среднее значение времени движения, как среднее арифметическое значение пяти последовательных измерений: 
.
Абсолютная погрешность измерения времени 
в каждом опыте (m = m1, m2, m3, m4):
(n=5).
Относительная погрешность измерения времени:
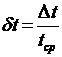для каждого из четырех опытов (m = m1, m2, m3, m4).
7. По найденным значениям t ср1, t ср2, t ср3, t ср4 для каждого груза m1, m2, m3, m4 вычислим соответствующие значения а1, а2, а3, а4, используя формулу 
.
8. По полученным значениям а1, а2, а3, а4 рассчитаем соответствующие значения момента силы (): М1, М2, М3, М4 и углового ускорения (): e 1, e 2, e 3, e 4 .
Таким образом, экспериментально получены координаты точек (М1, e 1), (М2, e 2), (М3, e 3), (М4, e 4).
9. Оценим погрешности экспериментального определения моментов сил М1, М2, М3, М4 и углового ускорения e 1, e 2, e 3, e 4. Поскольку определение величин моментов сил М и величины углового ускорения следует e из косвенных измерений, то используем зависимости относительной погрешности dМ и de от относительных погрешностей dr, dh, dt:
, 
, где 
.
Вычислив относительные погрешности d М1, d М2,d М3, d М4 и d e 1, d e 2,d e 3, d e 4, получим абсолютные погрешности измерения моментов сил М и углового ускорения e соответственно D М1, D М2,D М3, D М4 и D e 1, D e 2,D e 3, D e 4, используя формулы: 
и 
.
10. По точкам (М1, e 1), (М2, e 2), (М3, e 3), (М4, e 4) с учетом погрешностей экспериментального определения ускорения построим и проанализируем график зависимости 
.
Рис. 2. График экспериментальной зависимости 
Контрольные вопросы
1. Угол поворота, угловая скорость, угловое ускорение.
2. Момент инерции материальной точки и твердого тела.
3. Теорема Штейнера.
4. Момент силы. Плечо силы.
5. Момент количества движения.
6. Основной закон динамики вращательного движения.
7. График зависимости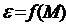 
в данной работе не проходит через начало координат! Почему?
