Компьютерное моделирование в нефтегазовом деле
Объект
Объектом ММ физические процессы имеющие место при работе технических систем. Например: движение сред, теплообмен и массообмен, деформация и устойчивость конструкций и т.д.
Цель построение и исследование математических моделей физических процессов происходящих в технических объектах и системах нефтегазового комплекса.
Методы исследования базируются на применении фундаментальных законов ньютоновской механики, теории тепло и массообмена, уравнениях состояния и аналитических зависимостей, описывающие многообразие изменения рабочих параметров в практических случаях.
Основой ММ являются математические уравнения, которые могут быть записаны в аналитической, дифференциальной и интегральной формах и дополнены условием однозначности, справедливым для изучаемого процесса. Исходя из условий задачи моделирования могут быть аналитические модели, модели с сосредоточенными параметрами, полевые и комбинированные модели.
В основе аналитических моделей – обыкновенные алгебраические зависимости вида f(x) = axn + bx + c, где f(x) – искомая целевая функция, x – аргумент этой функции, который меняется в процессе счета.
Основой ММ с сосредоточенными параметрами является обыкновенные дифференцированные уравнения (ОДУ)  f(x) =
f(x) = 
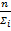
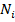
Основой полевых моделей являются дифференциальные уравнения частных производных (ДУЧП): f(x) = 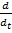 f(
f(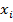 ) +
) +  f(
f(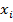 )
)
| ММ |




 – определяющие параметры, однозначно описывающие состояние и физическую сущность рассматриваемого процесса.
– определяющие параметры, однозначно описывающие состояние и физическую сущность рассматриваемого процесса.
 - целевая функция, значение которой определяется при реализации.
- целевая функция, значение которой определяется при реализации.
 - возмущающие факторы - совокупность внешних и внутренних факторов процесса изменение которых влияет на значение функции.
- возмущающие факторы - совокупность внешних и внутренних факторов процесса изменение которых влияет на значение функции.
 - управляющие факторы, значениями которого можно управлять в процессе моделирования.
- управляющие факторы, значениями которого можно управлять в процессе моделирования.
Порядок построения математической модели и компьютерная реализация
1. Набор исходных данных для построения ММ изучаемого процесса, включая анализ типовых процессов и физической картины.
2. Построение расчетных схем, введение ограничений и допущений.
3. Разработка ММ (запись систем уравнений) и расчетного алгоритма.
4. Реализация ММ на ЭВМ.
5. Реализация тестового примера.
6. Верификация полученных результатов и идентификация параметров ММ.
7. Решение произвольных задач в заданных условиях.
Пример 1.
Истечения через отверстия и насадки при переменном напоре (опорожнение сосудов)
Рассмотрим случай опорожнения открытого в атмосферу сосуда при постоянно уменьшающемся напоре, при котором течение является неустановившемся рис.1.
Однако если напор, а, следовательно, и скорость истечения изменяются медленно, то движение в каждый момент времени можно рассматривать как установившееся, и для решения задачи применить уравнение Бернулли.

Рис.1. - Схема опорожнения резервуара
Обозначим переменную высоту уровня жидкости в сосуде за h, площадь сечения резервуара на этом уровне S, площадь отверстия Sо, и взяв бесконечно малый отрезок времени dt, можно записать следующее уравнение объемов:

где dh - изменение уровня жидкости за время dt. Отсюда время полного опорожнения сосуда высотой Н:

Если будет известен закон изменения площади S по высоте h, то интеграл можно подсчитать. Для призматического сосуда S = const (рис.2), следовательно, время его полного опорожнения:

Из этого выражения следует, что время полного опорожнения призматического сосуда в два раза больше времени истечения того же объема жидкости при постоянном напоре, равном первоначальному.

| 
|
| Рис. 2 - Опорожнение призматического резервуара | Рис. 3. Опорожнение непризматического резервуара |
Для определения времени истечения жидкости из горизонтального цилиндрического сосуда (цистерны) (рис. 3) выразим зависимость переменной площади S от h:
 где l - длина цистерны; D - диаметр цистерны. Тогда время полного опорожнения такой цистерны, т.е. время изменения напора от h1 = D до h2 = 0, получится равным:
где l - длина цистерны; D - диаметр цистерны. Тогда время полного опорожнения такой цистерны, т.е. время изменения напора от h1 = D до h2 = 0, получится равным:

Программная реализация в расчетной системе.
Построение зависимостей вида H = f(t) для резервуаров призматического и непризматического вида.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 2.
Рассмотрим работу мокрого газгольдера.
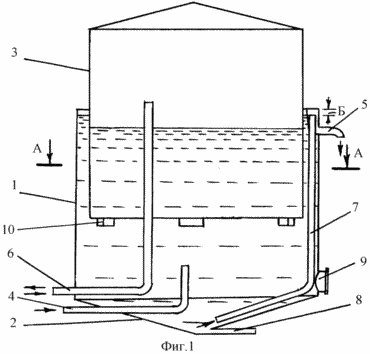

Мокрый газгольдер переменной емкости /фиг.1 и 2/ содержит резервуар 1 с конусным днищем 2 и с подъемно-опускаемым колоколом 3. В резервуаре 1 выполнены патрубки заполнения 4 и 5 опорожнения резервуара 1 проточной жидкостью, патрубок /патрубки/ подвода и отвода газа 6.
Заборная часть 7 патрубка опорожнения 5 резервуара 1 от проточной жидкости с осадком, выполненная в виде изогнутой трубы, нижний конец которой установлен в центре конусного днища 2, а верхний - вмонтирован в расширенную верхнюю часть изогнутого патрубка опорожнения 5 на расстоянии "Б" от верха резервуара 1 и несколько выше патрубка 5, что обеспечивает слив из резервуара 1 проточной жидкости, вытекающей с осадком с верхнего конца трубы заборной части 7. Для опорожнения резервуара от жидкости в днище 2 выполнен патрубок 8, а для периодической очистки днища 2 раз в 3-4 года от осадков снизу в стенке резервуара 1 выполнен люк с крышкой 9. Для установления регламентируемого СНиП давления газа в метантенках и газгольдерах к колоколу 3 снизу прикреплены съемные грузы 10, вес которых назначается с учетом диаметра и веса колокола 3.
Г азгольдеры объемом до 6000м3 включительно делаются обычно однозвенными (т.е. без телескопа), а при большем объеме – двухзвенными. Газ, поступающий в газгольдер, своим давлением поднимает колокол, который зацепляет затвором обратный затвор телескопа и начинает подниматься вместе с ним. При этом затвор колокола захватывает с собой воду из бассейна, в результате чего образуется газонепроницаемая подушки, противостоящая давлению газа в газгольдере. П равильное движение колокола и телескопа и ограничение их перекоса во время движения выполняются с помощью наружных (верхних) роликов, катящихся по внутренним направляющим. Внутренние ролики колокола в однозвенном газгольдере катятся по направляющим бассейна, в двухзвенном – по направляющим телескопа; внешние ролики в газгольдерах обоих видов катятся по направляющим бассейна. П ри отсутствии внутреннего давления колокол и телескоп опираются на особые подставки, установленные на дно бассейна под нижними кольцами колокола и телескопа. М аксимальное давление внутри газгольдера возникает при наивысшем положении колокола и зависит от веса колокола и телескопов, пригрузов, находящихся в затворах воды, объема и удельного веса газа, хранимого в газгольдере.
Математическая модель работы газгольдера основывается на составлении и реализации систем уравнений термодинамики.
Расчетная схема
Здесь h – высота колокола; d – внутренний диаметр колокола; m1г – массовый расход газа на входе; m2г – массовый расход газа, отбираемый из газгольдера.
Будем считать, что в качестве рабочего тела принимается газ, близкий по своим свойствам к идеальному газу. В этом случае будет связь между параметрами состояния определится уравнением состояния Менделеева – Клайперона:
pV=mRT
где p – абсолютное давление, Па; V – объем рабочей полости, м3; m – масса, кг;
R – удельная газовая постоянная, Дж/(кг К); T – абсолютная температура, К.
Задачей построения математической модели является исследование поведения функции h(t) – изменения высоты поднятия колокола от массового расхода газа, подаваемого m1г и отбираемый m2г из газгольдера.
Тогда запишем:  то
то  . Объем рабочей полости будет изменяться пропорционально балансу массовых расходов
. Объем рабочей полости будет изменяться пропорционально балансу массовых расходов  ,
,  .
.
 - плотность газа;
- плотность газа;  - время.
- время.
Отсюда имеем запись для h(t) - изменения высоты поднятия колокола от массового расхода газа:

Плотность газа выразим из уравнения состояния:
 , тогда
, тогда

Полученное соотношение будем использовать в качестве основанного для нахождения целевой функции h(t).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 3.
Рассмотрим работу испарителя.
Испаритель — теплообменный аппарат, в котором осуществляется процесс фазового перехода жидкого теплоносителя в парообразное и газообразное состояние за счёт подвода от более горячего теплоносителя. Таким горячим теплоносителем обычно являются вода, воздух, рассол или газообразные, жидкие или твердые технологические продукты. Когда процесс фазового перехода происходит на поверхности жидкости, то это называется испарением. Если процесс происходит на всей глубине жидкости с образованием паровых пузырьков, то это называется кипением. Фазовый переход может происходить как с однородной жидкостью, так и со смесью жидких компонентов. Испарители различаются по характеру происходящих в них процессов, а также по их назначению, и они при этом обычно имеют свои названия.

Математическая модель работы испарителя основывается на составлении и реализации систем уравнений термодинамики.
Расчетная схема
Здесь h – высота испарителя; d – внутренний диаметр; m1 – массовый расход пара при испарении; m2 – массовый расход пара при конденсации.
Будем считать, что в качестве рабочего тела принимается жидкость, близкая по своим свойствам к ньютоновской, например вода. В этом случае, преобразование воды в пар будет проходить в два этапа. Первый – нагрев воды до температуры насыщения, второй - переход из жидкого состояния в газообразное состояние.
Нагрев жидкости до температуры насыщения описывается уравнением теплового баланса:
ΔQ=cmΔTt
где ΔQ – подвод тепловой энергии, Вт; с – удельная теплоемкость, Дж/(кг град);
m – масса, кг; ΔT – перепад температур, град; t – время.
Тогда температура насыщения определится так:
dT/dt =ΔQ/cm
Теплота фазового перехода из жидкого состояния в газообразное при начальной температуре насыщения равна:
Q = mr
где r – удельная теплота парообразования, Дж/кг;
m – масса жидкости, нагретой до температуры насыщения, кг.
Задачей построения математической модели является исследование поведения функции h(t) – изменения высоты уровня жидкости от мощности нагревательного устройства и свойств жидкости.
Тепловую мощность нагревательного устройства определим так:
Q = N* ηE
где N – мощность теплового устройства (нагревателя), кВт;
ηE – тепловой эквивалент преобразования единицы работы устройства в тепловую энергию, 860 ккал/(кВт ч).
При достижении температуры жидкости равной температуре насыщения при заданном давлении имеем:

Полученное соотношение будем использовать в качестве основанного для нахождения целевой функции h(t).





 температура жидкости
температура жидкости

 время нагрева
время нагрева








 высота уровня жидкости снижается за счет испарения
высота уровня жидкости снижается за счет испарения
 время испарения
время испарения







Пример 4. Имплозионная обработка скважин
Алгоритм расчета величины давления гидравлического удара, создаваемого в призабойной зоне скважины за счет эффекта имплозии.
Величина давления определяется по формуле Н.Е. Жуковского:

где
ro – плотность жидкости, кг/м3;
w – скорость движения жидкости м/с;
с – скорость распространения ударной волны в трубах м/c.
Скорость движения нисходящего потока рабочей жидкости в нижней части имплозионной камеры определяется по формуле:

где
fi – коэффициент скорости (0,7 -0,9)
p0 =ro g H – статическое давление на шток на уровне подвески камеры;
Dk – внутренний диаметр имплозионной камеры
lam – коэффициент гидравлического сопротивления трения при движении скважинной жидкости по камере
lk – длина имплозионной камеры
Зная скорость нисходящего потока w рассчитывается давление гидравлического удара pg.
Величины давления получены при условии отсутствия зазора между эксплуатационной колонной и концентратором давления.
В случае наличия радиального зазора del давление снижается.
Величину потерь в зазоре можно оценить:

где
lk1 – длина концентратора давления, м;
del – величина радиального зазора, м;
w1 – скорость течения жидкости в зазоре, м/c.

mu – коэффициент истечения (0.7 – 0.9)
При разработке технологических мероприятий подбирают условия, при который давление гидравлического удара больше величины горного давления в месте перфорации.
Пример 5. Гидроудар
Гидравлический удар (гидроудар) в трубопроводе – это мгновенный скачок давления жидкости в напорных трубах, связанный с резким изменением скорости движения потока воды. В зависимости от направления скачка давления гидроудар разделяют на:
Положительный – давление в трубопроводе возрастает из-за резкого перекрытия трубы или включения насоса(рис.1);
Отрицательный – когда давление в трубопроводе падает из-за выключения насоса или открытия заслонки.
Явление гидравлического удара количественно описал в 1897—1899 г. Н. Е. Жуковский. Увеличение давления при гидравлическом ударе определяется в соответствии с его теорией по формуле:
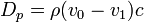 ,
,
где  — увеличение давления в Н/м²,
— увеличение давления в Н/м²,  — плотность жидкости в кг/м³,
— плотность жидкости в кг/м³,  и
и 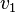 — средние скорости в трубопроводе до и после закрытия задвижки (запорного клапана) в м/с, с — скорость распространения ударной волны вдоль трубопровода.
— средние скорости в трубопроводе до и после закрытия задвижки (запорного клапана) в м/с, с — скорость распространения ударной волны вдоль трубопровода.
Жуковский доказал, что скорость распространения ударной волны c находится в прямо пропорциональной зависимости от сжимаемости жидкости, величины деформации стенок трубопровода, определяемой модулем упругости материала, из которого он выполнен, а также от диаметра трубопровода. Следовательно, гидравлический удар не может возникнуть в трубопроводе, содержащем газ, так как газ легко сжимаем. Зависимость между скоростью ударной волны c, её длиной и временем распространения (L и 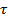 соответственно) выражается следующей формулой:
соответственно) выражается следующей формулой:
c = 2 L / 𝜏,
Положительный гидроудар.

В зависимости от времени распространения ударной волны 𝜏 и времени перекрытия задвижки (или другой запорной арматуры) t, в результате которого возник гидроудар, можно выделить 2 вида ударов:
Полный (прямой) гидравлический удар, если t < 𝜏
Неполный (непрямой) гидравлический удар, если t > 𝜏
При полном гидроударе фронт возникшей ударной волны движется в направлении, обратном первоначальному направлению движения жидкости в трубопроводе. Его дальнейшее направление движения зависит от элементов трубопровода, расположенных до закрытой задвижки. Возможно и повторное неоднократное прохождения фронта волны в прямом и обратном направлениях. При неполном гидроударе фронт ударной волны не только меняет направление своего движения на противоположное, но и частично проходит далее сквозь не до конца закрытую задвижку.
Математическая модель
Расчет гидравлического удара. Прямой гидравлический удар бывает тогда, когда время закрытия задвижки t3 меньше фазы удара T, определяемой по формуле: T =2l/Cu,
Здесь l - длина трубопровода от места удара до сечения, в котором поддерживается постоянное давление, Cu - скорость распространения ударной волны в трубопроводе, определяется по формуле Н.Е. Жуковского, м/с:

где E - модуль объемной упругости жидкости, p - плотность жидкости, √(E/p) - скорость распространения звука в жидкости, Etr - модуль упругости материала стенок трубы, D - диаметр трубы, h - толщина стенок трубы.
Для воды отношение E/Etr зависит от материала труб и может быть принято; для стальных - 0.01; чугунных - 0.02; ж/б - 0.1-0.14; асбестоцементных - 0.11; полиэтиленовых - 1-1.45
Коэффициент k для тонкостенных трубопроводов применяется (стальные, чугунные, а/ц, полиэтиленовые) равным 1.
Повышение давления при прямом гидравлическом ударе определяется по формуле:
P=pCuVo,
где V0 - скорость движения воды в трубопроводе до закрытия задвижки.
Если время закрытия задвижки больше фазы удара (t3>Т), такой удар называется непрямым. В этом случае дополнительное давление может быть определено по формуле:
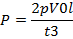
Результат действия удара выражают также величиной повышения напора H, которая равна:
при прямом ударе 
при непрямом 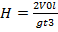
| ММ |



 – определяющие параметры, однозначно описывающие состояние и физическую сущность рассматриваемого процесса.
– определяющие параметры, однозначно описывающие состояние и физическую сущность рассматриваемого процесса.
 - целевая функция, значение которой определяется при реализации.
- целевая функция, значение которой определяется при реализации.
 - возмущающие факторы - совокупность внешних и внутренних факторов процесса изменение которых влияет на значение функции.
- возмущающие факторы - совокупность внешних и внутренних факторов процесса изменение которых влияет на значение функции.
Реализация ММ в Mathcad
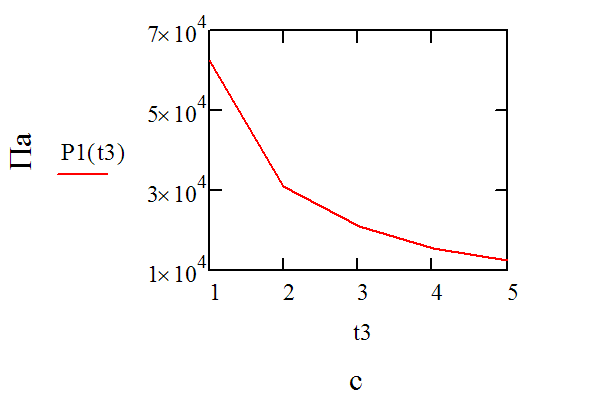
В качестве целевой функции выберем P(V0), H(V0), P1(t3), H1(t3), зависимость повышения давления и величину повышения напора от скорости движения жидкости в трубе и времени закрытия заслонки.
Исходные данные:
-Модуль объёмной упругости (вода) Е=2,2•109Па
-Плотность(вода) р=1040 кг/м3
-Диаметр трубопровода D=0,073 м
-Толщина стенки трубы h=0,0055 м
-Расстояние от заслонки до точки в трубе где сохраняется постоянное давление l=30 м
-Ускорение свободного падения g=9,8 м/с2
-Скорость движения жидкости в трубопроводе V0=1… 5 м/с
-Время закрытия задвижки t3=1… 5 c
Программная реализация ММ (MathCAD)
| Вычисление | Результат | Наименование | Единицы измерения |
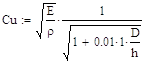
| 
| Скорость распространения ударной волны в трубопроводе | м/с |

| 
| Фаза удара | с |
Рассмотрим влияние скорости движения жидкости в трубе и времени закрытия заслонки на P(V0), H(V0), P1(t3), H1(t3).










|
|
Вывод
Повышение давления и напора зависит от скорости движения жидкости, времени закрытия заслонки. Следовательно, чтобы уменьшить негативное влияние гидроудара следует уменьшить скорость движения жидкости или увеличить время закрытия заслонки.
Список использованной литературы
1. «Основы гидравлики и аэродинамики», Калицун В. И., Дроздов Е. В., Комаров А. С., Чижик К. И., «Стройиздат», 2002 г.
2. «Сборник задач по гидравлике», под ред. В.А. Большакова, 1979. 336с.
3. Жуковский Н.Е. О гидравлическом ударе в водопроводных трубах, 1899
































