Определение
Пусть дано отображение 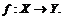 Тогда множество
Тогда множество 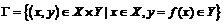 называется графиком отображения
называется графиком отображения 
Для построения графика функции, вообще говоря, необходимо использовать аппарат дифференциального исчисления. Однако в простых случаях эскиз графика может быть построен достаточно точно (т.е. с определением характерных особенностей данной функции) и без привлечения производных. Полезно начать построение с исследования основных свойств рассматриваемой функции: установления области её определения и, если возможно, области значений, проверки функции на чётность-нечётность, периодичность.
Иногда при построении эскизов графиков функций можно воспользоваться известным графиком другой функции: 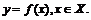 В приведённой ниже таблице описано, как изменится этот график при определённом преобразовании функции
В приведённой ниже таблице описано, как изменится этот график при определённом преобразовании функции 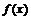 или её аргумента.
или её аргумента.
Функция 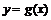
| Преобразование графика функции 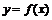
|

| Сдвиг вдоль оси ординат на 
|
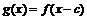
| Сдвиг вдоль оси абсцисс на 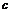
|
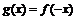
| Симметрия относительно оси ординат |
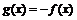
| Симметрия относительно оси абсцисс |
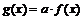
| Растяжение вдоль оси  относительно оси относительно оси 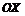 в в 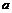 раз при раз при  либо сжатие в либо сжатие в 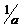 раз при раз при 
|
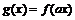
| Сжатие в 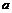 раз при раз при  либо растяжение в либо растяжение в 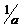 раз при
раз при  вдоль оси вдоль оси 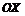 относительно оси относительно оси 
|
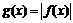
| Часть графика функции 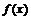 , расположенную ниже оси , расположенную ниже оси 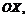 симметрично отобразить относительно оси симметрично отобразить относительно оси 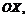 остальную часть оставить без изменений остальную часть оставить без изменений
|
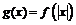
| Часть графика функции 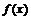 , лежащую справа от оси , лежащую справа от оси 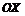 (при (при  ), симметрично отобразить относительно оси ), симметрично отобразить относительно оси  в область в область 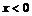 , удалив при этом часть графика , удалив при этом часть графика 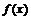 , лежащую слева от оси , лежащую слева от оси 
|
Очевидно, что графики функций 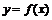 и обратной для неё
и обратной для неё 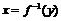 совпадают. Если и для обратной функции мы обозначим аргумент через
совпадают. Если и для обратной функции мы обозначим аргумент через 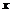 , т.е. будем рассматривать функцию
, т.е. будем рассматривать функцию 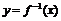 , то графически это будет означать, что мы как бы переставили оси местами. Этот процесс легко осуществить, если повернуть плоскость чертежа на
, то графически это будет означать, что мы как бы переставили оси местами. Этот процесс легко осуществить, если повернуть плоскость чертежа на 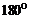 вокруг биссектрисы первого координатного угла. Таким образом, график функции
вокруг биссектрисы первого координатного угла. Таким образом, график функции 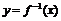 симметричен графику функции
симметричен графику функции 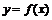 относительно прямой
относительно прямой  .
.
Проиллюстрируем данную таблицу примерами.
Пример 1. Построить эскиз графика функции 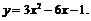
После элементарных преобразований  проведём следующее построение: 1) изобразим график функции
проведём следующее построение: 1) изобразим график функции  2) произведём растяжение в 3 раза вдоль оси
2) произведём растяжение в 3 раза вдоль оси  относительно оси
относительно оси 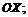 3) сдвинем ось
3) сдвинем ось  на единицу влево и ось
на единицу влево и ось 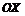 на 4 вверх. В результате получим график данной функции (рис. 1).
на 4 вверх. В результате получим график данной функции (рис. 1).
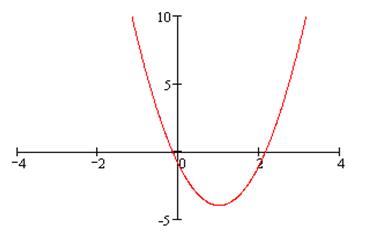
Рис. 1
Пример 2. Построить эскиз графика функции 
Так как  то требуемый график может быть получен из графика функции
то требуемый график может быть получен из графика функции 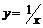 путём следующих преобразований: 1) симметрично отобразить относительно оси
путём следующих преобразований: 1) симметрично отобразить относительно оси 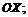 2) осуществить растяжение вдоль оси
2) осуществить растяжение вдоль оси  относительно оси
относительно оси 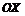 в 3 раза; 3) сдвинуть ось
в 3 раза; 3) сдвинуть ось  на 2 единицы влево и ось
на 2 единицы влево и ось 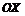 на 4 единицы вверх. График изображён на рис. 2 (пунктиром обозначены асимптоты).
на 4 единицы вверх. График изображён на рис. 2 (пунктиром обозначены асимптоты).

Рис. 2
Пример 3. Построить эскиз графика функции 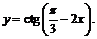
Учитывая нечётность функции 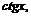 получим:
получим:
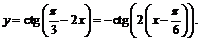 Для построения графика данной функции необходимо: 1) построить график функции
Для построения графика данной функции необходимо: 1) построить график функции 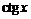 ; 2) сжать его вдоль оси
; 2) сжать его вдоль оси 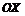 относительно оси
относительно оси  в 2 раза; 3) сдвинуть ось
в 2 раза; 3) сдвинуть ось  на
на 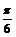 влево; 4) симметрично отобразить относительно оси
влево; 4) симметрично отобразить относительно оси 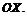
Полученный график представлен на рис. 3 (пунктиром изображены асимптоты – прямые 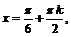
 ).
).
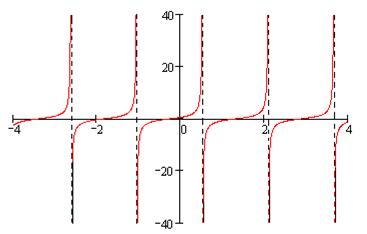
Рис. 3
Пример 4. Построить график функции 
Областью определения данной функции является: 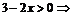
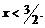 Нуль функции:
Нуль функции: 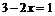

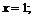 при
при 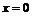
 Функция убывающая.
Функция убывающая.  Поэтому: 1) строим график функции
Поэтому: 1) строим график функции  2) производим сжатие этого графика вдоль оси
2) производим сжатие этого графика вдоль оси 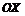 относительно оси
относительно оси  в два раза; 3) отображаем график симметрично относительно оси
в два раза; 3) отображаем график симметрично относительно оси  4) сдвигаем ось
4) сдвигаем ось  на 1,5 единицы влево вдоль оси
на 1,5 единицы влево вдоль оси 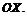 Полученный график изображён на рис. 4 (пунктирная линия – асимптота
Полученный график изображён на рис. 4 (пунктирная линия – асимптота 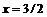 данной функции).
данной функции).
Отметим здесь важный момент: величина сдвига графика вдоль оси 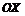 (или оси
(или оси  вдоль оси
вдоль оси 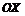 ) определяется той константой, которая прибавляется непосредственно к аргументу
) определяется той константой, которая прибавляется непосредственно к аргументу  а не к аргументу
а не к аргументу  Поэтому сначала необходимо совершить преобразование
Поэтому сначала необходимо совершить преобразование  к виду
к виду 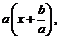 а при построении графика операцию сдвига вдоль оси
а при построении графика операцию сдвига вдоль оси 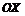 всегда проводить после операции сжатия либо растяжения вдоль оси
всегда проводить после операции сжатия либо растяжения вдоль оси 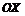 относительно оси
относительно оси 
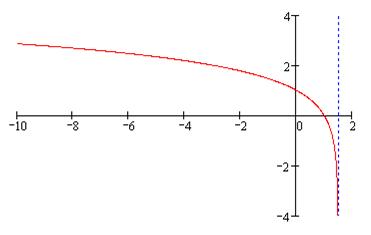
Рис. 4
Пример 5. Построить график функции 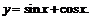

Рис.5
После простейших преобразований получим:
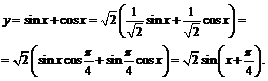
Теперь построим график функции  затем сдвинем ось
затем сдвинем ось  вправо на
вправо на  и, наконец, произведём растяжение полученного графика вдоль оси
и, наконец, произведём растяжение полученного графика вдоль оси  относительно оси
относительно оси 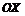 в
в 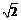 раз. График функции
раз. График функции  представлен на рис. 5.
представлен на рис. 5.
Пример 6. Изобразить график функции 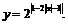
Выпишем цепочку требуемых преобразований:
а)  б)
б)  в)
в) 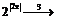 г)
г) 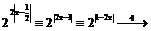
д)  е)
е) 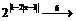 ж)
ж) 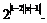
Необходимые операции: 1 - сжатие вдоль оси 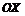 относительно оси
относительно оси  в два раза; 2, 4, 6 – отображение части графика, лежащей справа от оси
в два раза; 2, 4, 6 – отображение части графика, лежащей справа от оси  симметрично относительно оси
симметрично относительно оси  в область
в область 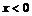 и удаление части графика, лежащей слева от оси
и удаление части графика, лежащей слева от оси  3 – сдвиг оси
3 – сдвиг оси  влево на
влево на  5 – сдвиг оси
5 – сдвиг оси  влево на единицу.
влево на единицу.
На рис. 6 (а-е) приведены эскизы графиков соответствующих функций:

Рис. 6а Рис. 6б
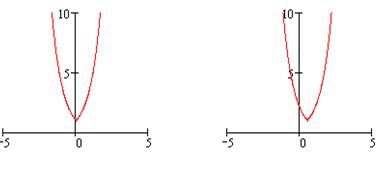
Рис. 6в Рис. 6г

Рис. 6д Рис. 6е
график функции  изображён на рис. 6ж.
изображён на рис. 6ж.
Кроме случаев преобразования известного графика функции, представленных в таблице, существуют и другие приёмы. Например, если известен график функции  то его можно использовать при построении графика
то его можно использовать при построении графика 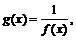 ибо значения функции
ибо значения функции 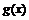 обратны значениям функции
обратны значениям функции  Это может продемонстрировать рис. 7, где представлены графики функции
Это может продемонстрировать рис. 7, где представлены графики функции  (пунктир),
(пунктир),  (сплошная линия).
(сплошная линия).

Рис. 6ж

Рис. 7
Пример 7. Построить график функции 
На рис. 8а представлен график функции  (пунктиром изображены асимптоты). Значения функции
(пунктиром изображены асимптоты). Значения функции 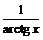 обратны значениям функции
обратны значениям функции 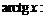 на промежутках
на промежутках  и
и  функция убывает,
функция убывает, 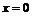 - вертикальная асимптота,
- вертикальная асимптота,  и
и 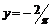 - горизонтальные асимптоты графика
- горизонтальные асимптоты графика 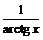 (рис. 8б).
(рис. 8б).
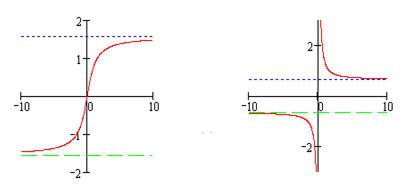
Рис. 8а Рис. 8б
Отобразим часть данного графика, лежащую справа от оси  (т.е. при
(т.е. при 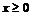 ), симметрично относительно оси
), симметрично относительно оси  в область
в область 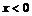 (рис. 8в). Далее перенесём ось
(рис. 8в). Далее перенесём ось  на единицу влево, получим
на единицу влево, получим

Рис. 8в Рис. 8г
график функции  (рис. 8г). Наконец, часть полученного графика, лежащую справа от оси
(рис. 8г). Наконец, часть полученного графика, лежащую справа от оси  отображаем симметрично относительно оси
отображаем симметрично относительно оси  в область
в область  На рис. 8д изображён график функции
На рис. 8д изображён график функции 

Рис. 8д
Иногда при построении графика сложной функции 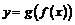 удобно построить сначала графики функций
удобно построить сначала графики функций 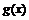 и
и 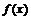 как вспомогательные.
как вспомогательные.
Пример 8. Построить график функции 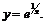
На рис. 9 а,б приведены графики функций  и
и 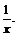 Функция
Функция 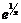 определена для всех
определена для всех  При
При  (слева) функция
(слева) функция  а тогда
а тогда 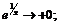 при
при 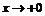 (справа) функция
(справа) функция
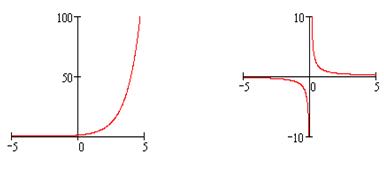
Рис. 9а Рис. 9б
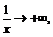 а значит
а значит  Когда
Когда 
 а, следовательно,
а, следовательно,  (к 1 слева, оставаясь меньше единицы), при
(к 1 слева, оставаясь меньше единицы), при 
 и
и 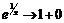 (к 1 справа, оставаясь больше 1). Прямая
(к 1 справа, оставаясь больше 1). Прямая 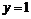 является горизонтальной асимптотой функции
является горизонтальной асимптотой функции 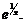 Учитывая интервалы монотонности функций
Учитывая интервалы монотонности функций  и
и 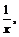 получим, что функция
получим, что функция 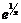 является монотонно убывающей на интервалах
является монотонно убывающей на интервалах 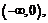
 Её график вместе с асимптотой (пунктирная линия) приведён на рис. 9в.
Её график вместе с асимптотой (пунктирная линия) приведён на рис. 9в.
Пример 9. Построить график функции 
Строим вспомогательные графики функций  и
и 
(рис. 10а,б). Областью определения функции  являются промежутки
являются промежутки 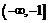 и
и  Функция чётная, поэтому достаточно изобразить её при
Функция чётная, поэтому достаточно изобразить её при 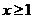 . Из монотонности вспомогательных функций следует, что функция
. Из монотонности вспомогательных функций следует, что функция 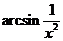
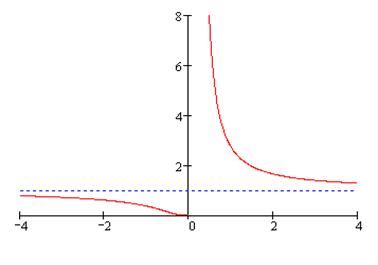
Рис. 9в
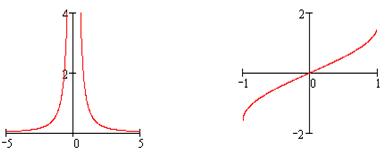
Рис. 10а Рис. 10б
является убывающей на 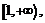 при
при 
 и
и 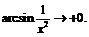 Ось
Ось 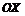 является горизонтальной асимптотой функции
является горизонтальной асимптотой функции  График функции представлен на рис. 10 в.
График функции представлен на рис. 10 в.
Для некоторых функций может быть применён приём «сложения графиков», когда на основе графиков функций 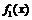 и
и 

Рис.10в
строится график функции  Продемонстрируем этот способ для гиперболический функций.
Продемонстрируем этот способ для гиперболический функций.
Функции 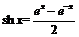 и
и  =
= 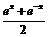 , определённые на
, определённые на  , называются гиперболическим синусом и гиперболическим косинусом.
, называются гиперболическим синусом и гиперболическим косинусом.
Функция  – нечётная, строго возрастающая, функция
– нечётная, строго возрастающая, функция 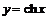 –чётная, строго убывающая на
–чётная, строго убывающая на  и строго возрастающая на
и строго возрастающая на  , в точке
, в точке 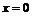 имеет минимум –
имеет минимум – 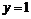 . Графики этих функций представлены на рисунках 11-12. Пунктирные кривые на рис. 11 отвечают функциям
. Графики этих функций представлены на рисунках 11-12. Пунктирные кривые на рис. 11 отвечают функциям 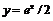 и
и  , а на рис. 12 - функциям
, а на рис. 12 - функциям 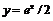 и
и  .
.
Гиперболические тангенс и котангенс определяются формулами:
 =
= 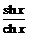 ,
,  ,
,  =
=  ,
,  ,
, 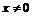 .
.
Обе функции нечётные,  монотонно возрастает, а
монотонно возрастает, а  монотонно убывает, их графики изображены на рисунках 13,14 (пунктиром обозначены асимптоты функций):
монотонно убывает, их графики изображены на рисунках 13,14 (пунктиром обозначены асимптоты функций):
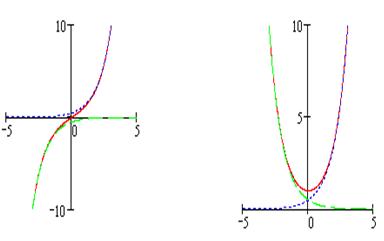
Рис. 11 Рис. 12

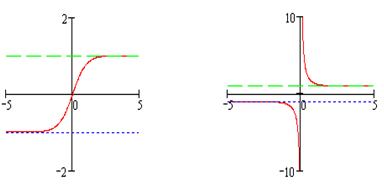
Рис. 13 Рис. 14
Название этих функций – синус, косинус, тангенс, котангенс – связано с тем, что эти функции имеют ряд свойств, аналогичных свойствам тригонометрических функций. Так, имеют место формулы (обратить внимание на знаки!):
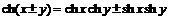 ,
, 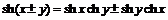 ,
,
из них, в частности, при 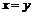 , следует:
, следует:

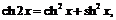
 .
.
Докажем, например, первую из этих формул:
 =
= 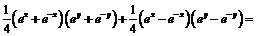

 . Так же проверяются и остальные.
. Так же проверяются и остальные.
Запишем ещё ряд формул для гиперболических функций:
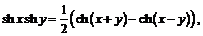
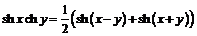 ,
, 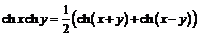 ,
,  , откуда
, откуда  ,
, 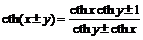 , откуда
, откуда 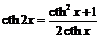 ,
,  ,
, 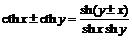 .
.
Функции  и
и 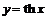 ,
,  , обратимы, их обратные функции обозначаются соответственно
, обратимы, их обратные функции обозначаются соответственно 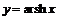 (ареасинус гиперболический) и
(ареасинус гиперболический) и  (ареатангенс гиперболический). Действительно, решая уравнение
(ареатангенс гиперболический). Действительно, решая уравнение
 или
или 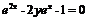 относительно
относительно  , найдём
, найдём  , откуда, выбирая знак «+» перед радикалом, ведь
, откуда, выбирая знак «+» перед радикалом, ведь  , получим
, получим 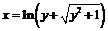 .
.
Аналогично из уравнения 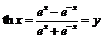 или
или 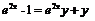 найдём
найдём  , откуда
, откуда 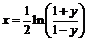 ,
,  .
.
Графики функций 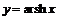 и
и  (а, значит, и найденных функций
(а, значит, и найденных функций  и
и 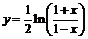 ) изображены на рисунках 15 и 16 (пунктирные линии на рис.16 отвечают асимптотам функции
) изображены на рисунках 15 и 16 (пунктирные линии на рис.16 отвечают асимптотам функции  ).
).
Рассмотрим функции 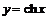 и
и 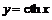 . Решая уравнение
. Решая уравнение
 или
или 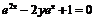 относительно
относительно  , найдём при
, найдём при
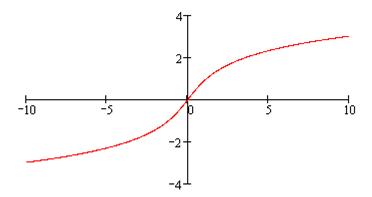
Рис. 15
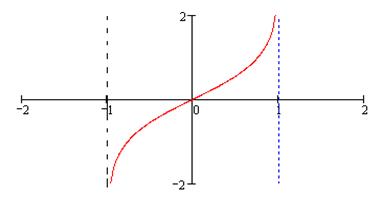
Рис. 16
 два значения
два значения  , откуда
, откуда 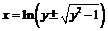 - получим двузначную функцию, которая распадается на две однозначных ветви:
- получим двузначную функцию, которая распадается на две однозначных ветви: 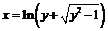 - обратная для
- обратная для 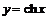 на
на  и
и 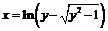 - обратная для
- обратная для 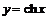 на
на  . На рис. 17 изображён график функций
. На рис. 17 изображён график функций  (сплошная линия) и
(сплошная линия) и
 (пунктирная кривая):
(пунктирная кривая):

Рис. 17
Из уравнения 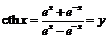 или
или 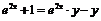 найдём:
найдём: 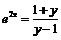 , откуда
, откуда 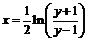 ,
, 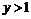 .
.
График функции  приведён на рис. 18 (пунктиром обозначены асимптоты данной функции).
приведён на рис. 18 (пунктиром обозначены асимптоты данной функции).
Эпитет «гиперболический» в названии рассмотренных функций связан с тем, что формулы 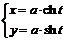 параметрически задают гиперболу
параметрически задают гиперболу 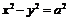 - каноническое уравнение гиперболы.
- каноническое уравнение гиперболы.
Если требуется построить график функции 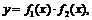 то
то
для некоторых функций 
 удобно использовать тот
удобно использовать тот
факт, что ординаты его точек получаются перемножением ординат
точек графиков 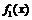 и
и 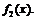 Особенно удобно
Особенно удобно

Рис. 18
руководствоваться этим способом, если 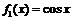 либо
либо 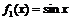 . Приведём пример.
. Приведём пример.
Пример 10. Построить график функции 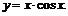
Функция нечётная, поэтому построим график при 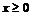 и воспользуемся симметрией относительно начала координат. Нули функции:
и воспользуемся симметрией относительно начала координат. Нули функции: 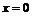 и
и 
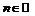 . Так как
. Так как  то
то 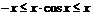
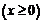 и график лежит между прямыми
и график лежит между прямыми 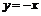 и
и  . При
. При 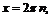
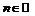 точки графика лежат на прямой
точки графика лежат на прямой 
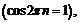 а при
а при 
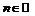 график имеет общие точки с прямой
график имеет общие точки с прямой 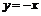 . На промежутке
. На промежутке 

 - график расположен ниже графиков
- график расположен ниже графиков 
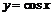 . В точке
. В точке 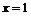 график
график 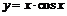 пересекает график
пересекает график  при этом
при этом  . Для
. Для 
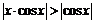 в точках, где
в точках, где  . На рис. 19 приведён график функции
. На рис. 19 приведён график функции 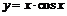 (сплошная линия). Пунктиром изображёны графики функций
(сплошная линия). Пунктиром изображёны графики функций  и
и  График данной функции представляет собой кривую, колеблющуюся между прямыми
График данной функции представляет собой кривую, колеблющуюся между прямыми  и
и 

Рис. 19
Введём в рассмотрение ещё две функции, не являющиеся элементарными, но играющими в математике заметную роль.
1) 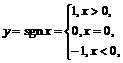 (читается «сигнум
(читается «сигнум 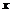 »).
»).
График этой функции представлен на рис. 20.


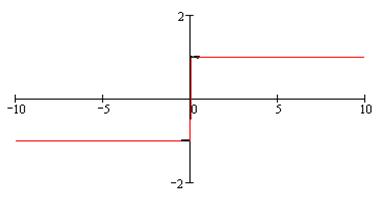
Рис. 20
2) Определим функцию 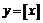 (читается «целая часть
(читается «целая часть 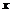 ») следующим образом:
») следующим образом:
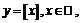 где
где  - наибольшее целое, не превосходящее
- наибольшее целое, не превосходящее 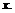 Иногда эту функцию обозначают
Иногда эту функцию обозначают 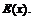 Так как
Так как 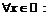
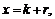









 где
где 
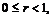 то согласно определению этой функции:
то согласно определению этой функции:  Таким образом, при
Таким образом, при 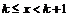 имеем:
имеем: 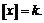 Рис. 21
Рис. 21




 График этой функции изображён на рис. 21.
График этой функции изображён на рис. 21.
В следующих примерах изобразить эскизы графиков функций, используя любые из вышеописанных приёмов.
Пример 11. Построить эскиз графика функции 
Функция нечётная, непериодическая. Найдём нули функции: 

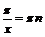

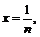

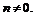 Функция имеет бесконечно много нулей, причём все они расположены на отрезке
Функция имеет бесконечно много нулей, причём все они расположены на отрезке  расстояние между двумя соседними нулями равно
расстояние между двумя соседними нулями равно 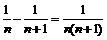 и с ростом
и с ростом  стремится к
стремится к 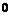 . Таким образом, в любой окрестности точки
. Таким образом, в любой окрестности точки 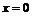 имеется бесконечно много нулей данной функции.
имеется бесконечно много нулей данной функции.
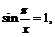 если
если 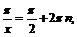

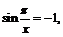 если
если 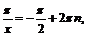


Все точки, где 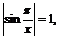 сосредоточены на отрезке
сосредоточены на отрезке 
При 
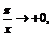 а, следовательно,
а, следовательно,  График данной функции приведён на рис. 22.
График данной функции приведён на рис. 22.
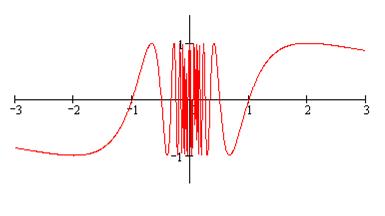
Рис. 22
Пример 12. Построить график функции 
Данный график может быть построен с использованием приёма перемножения ординат точек графиков функций  и
и  Изобразим сначала график функции
Изобразим сначала график функции 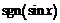 . По определению функции
. По определению функции  имеем:
имеем:

 График этой функции представлен на рис. 23.
График этой функции представлен на рис. 23.
Тогда 

Отметим, что рассматриваемая функция чётная, её график
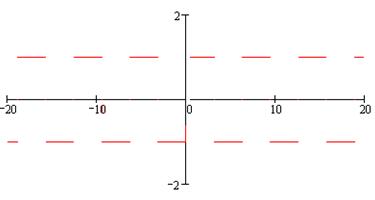
Рис. 23
изображён на рис. 24.
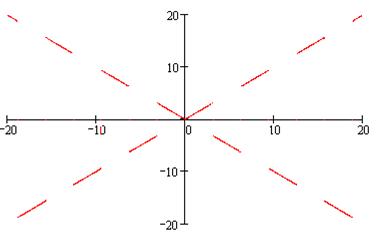 Рис. 24
Рис. 24
Пример 13. Построить график функции 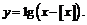
Для построения графика данной функции воспользуемся вспомогательным графиком функции 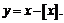 Согласно определению функции
Согласно определению функции  для
для 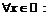
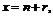

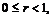 а
а  Поэтому
Поэтому 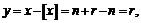

 - функция периодическая с периодом 1. График этой функции приведён на рис. 25. Областью её значений является промежуток
- функция периодическая с периодом 1. График этой функции приведён на рис. 25. Областью её значений является промежуток 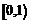 . Следовательно, областью значений функции
. Следовательно, областью значений функции 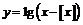 является интервал
является интервал 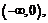 при этом функция монотонно возрастает, прямые
при этом функция монотонно возрастает, прямые 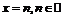 - суть асимптоты графика рассматриваемой функции, который представлен на рис. 26.
- суть асимптоты графика рассматриваемой функции, который представлен на рис. 26.
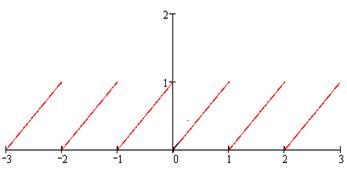


Рис.25
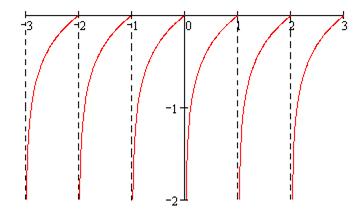
Рис.26
Пример 14. Построить график функции 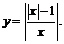
Начнём с построения графика функции 
 С этой целью график функции
С этой целью график функции  для
для  сместим на единицу вверх, а для
сместим на единицу вверх, а для 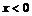 сдвинем
сдвинем
на единицу вниз, получим график функции 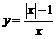 (рис. 27а).
(рис. 27а).
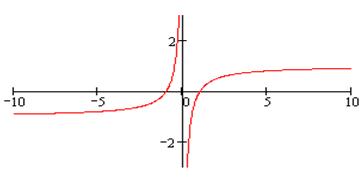
Рис. 27а
Чтобы построить требуемый график  , отобразим часть графика функции
, отобразим часть графика функции 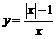 , расположенную ниже оси
, расположенную ниже оси 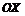 (т.е. при
(т.е. при  и
и 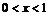 ), симметрично относительно этой оси, остальную часть графика оставим без изменений. На рис. 27б изображён график функции
), симметрично относительно этой оси, остальную часть графика оставим без изменений. На рис. 27б изображён график функции 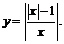 Отметим, что данный эскиз может быть построен другим способом с помощью следующей цепочки преобразований:
Отметим, что данный эскиз может быть построен другим способом с помощью следующей цепочки преобразований: 

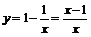

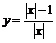

 .
.
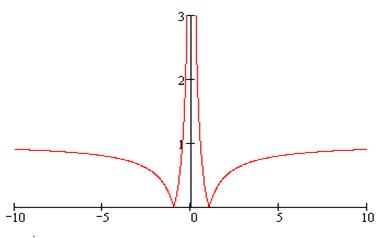
Рис. 27б
Пример 15. Построить график функции 
Область определения данной функции:  при
при 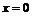

Из тождества 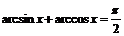 при
при  получим:
получим:
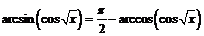 (так как
(так как 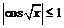 для
для 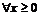 ).
).
Поскольку  при
при 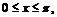 то
то  при
при  т.е. при
т.е. при  Следовательно, на отрезке
Следовательно, на отрезке 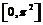

Если  то
то 

Используя формулу приведения 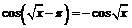 и тождество
и тождество 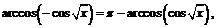 будем иметь:
будем иметь:
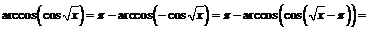

Итак, при 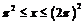
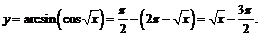
На отрезке 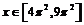 получим:
получим: 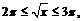
 и, так как
и, так как  то
то

Тогда  при
при 
Рассуждая аналогично, для 
 ,
,  получим, что график рассматриваемой функции совпадает с графиком функции
получим, что график рассматриваемой функции совпадает с графиком функции 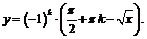
Окончательный эскиз графика функции  представлен на рис. 28.
представлен на рис. 28.

Рис. 28
Пример 16. Построить график функции 
На рис. 29а строим графики функций  (сплошная линия)
(сплошная линия)
и 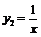 (пунктирная линия).
(пунктирная линия).
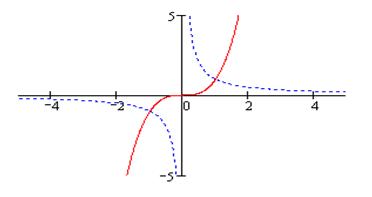
Рис. 29а
Точками пересечения этих кривых являются: т. 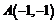 и т.
и т.  При
При 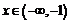 и
и 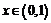
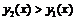 и значит
и значит 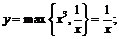 а на промежутках
а на промежутках  и
и 
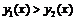 и, следовательно,
и, следовательно,  График функции изображён на рис. 29б.
График функции изображён на рис. 29б.
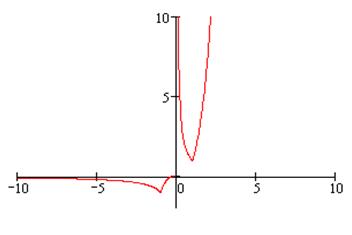
Рис. 29б
Пример 17. Построить график функции 
На рис. 30а изображены графики функций 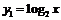 (сплошная линия) и
(сплошная линия) и  (пунктирная линия).
(пунктирная линия).
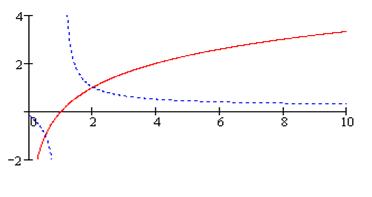
Рис. 30а
Точками пересечения кривых являются точки  и
и 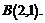 На промежутках
На промежутках  и
и 
 значит
значит 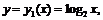 а на интервалах
а на интервалах  и
и 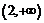
 следовательно,
следовательно,  График данной функции представлен на рис. 30б.
График данной функции представлен на рис. 30б.
Кроме привычной декартовой прямоугольной системы координат на плоскости существует и полярная система координат, являющаяся криволинейной.
Зафиксируем на плоскости луч 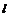 с началом в точке
с началом в точке  . Назовём этот луч полярной осью, а точку
. Назовём этот луч полярной осью, а точку






