Определение функции
Определение отношения
Пусть  и
и  - произвольные множества. Каждое подмножество прямого произведения
- произвольные множества. Каждое подмножество прямого произведения 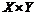 называется отношением или соответствием.
называется отношением или соответствием.
Для отношения используется обозначение  , где
, где 
 либо
либо 
Определение
Множество пар  данного отношения
данного отношения  называется графиком отношения
называется графиком отношения 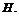
Например, пусть  - множество букв русского алфавита, а
- множество букв русского алфавита, а  . Отношение
. Отношение  сопоставляет каждой букве её порядковый номер.
сопоставляет каждой букве её порядковый номер.
Первый элемент пары  называют первой проекцией пары, второй элемент пары – второй проекцией. Множество всех первых проекций отношения называется областью определения отношения
называют первой проекцией пары, второй элемент пары – второй проекцией. Множество всех первых проекций отношения называется областью определения отношения  , множество всех вторых проекций – множеством значений отношения. Очевидно, область определения принадлежит
, множество всех вторых проекций – множеством значений отношения. Очевидно, область определения принадлежит  ,
,
область значений содержится в 
Определение
Отношение  называется рефлексивным, если для
называется рефлексивным, если для  имеет место
имеет место 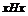 .
.
Определение
Отношение  называется симметричным, если для
называется симметричным, если для 

влечёт  .
.
Определение
Отношение  называется транзитивным, если для
называется транзитивным, если для  выполняется импликация:
выполняется импликация: 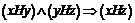 .
.
Определение
Отношение  называется отношением эквивалентности, если оно рефлексивно, симметрично и транзитивно одновременно.
называется отношением эквивалентности, если оно рефлексивно, симметрично и транзитивно одновременно.
Приведем примеры.
1. Отношение знакомства: рефлексивно, симметрично, но не является транзитивным.
2. Отношение включения множеств  рефлексивно и транзитивно, но не является симметричным.
рефлексивно и транзитивно, но не является симметричным.
3. Отношение порядка во множестве вещественных чисел:  - рефлексивно
- рефлексивно  , транзитивно, но не симметрично.
, транзитивно, но не симметрично.
4. Отношение перпендикулярности отрезков на плоскости симметрично, но не является рефлексивным и транзитивным.
5. Отношение параллельности отрезков на плоскости является отношением эквивалентности.
6. Отношение равенства между множествами является отношением эквивалентности.
Определение функции
Отношение  , определённое на множестве
, определённое на множестве  и обладающее свойством: если у двух пар
и обладающее свойством: если у двух пар  ,
,  совпадают первые элементы
совпадают первые элементы  то у них совпадают и вторые элементы
то у них совпадают и вторые элементы  , называется отображением множества
, называется отображением множества  во множество
во множество  Множество
Множество  называется областью определения отображения, элемент
называется областью определения отображения, элемент 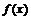 называют образом
называют образом 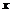 при этом отображении,
при этом отображении,  - множество образов всех элементов
- множество образов всех элементов  или множество значений отображения.
или множество значений отображения.
Для отображения приняты следующие обозначения:  ,
,  .
.
Отметим, что определённое таким образом отображение является однозначным.
В качестве множеств  и
и  могут выступать объекты любой природы. Если
могут выступать объекты любой природы. Если  и
и  то такое отображение называется функцией (или числовой функцией числового аргумента). Если же
то такое отображение называется функцией (или числовой функцией числового аргумента). Если же  ,
,  то имеем числовую функцию векторного аргумента или функцию многих переменных. Когда и
то имеем числовую функцию векторного аргумента или функцию многих переменных. Когда и  и
и  то такая функция называется векторной функцией векторного аргумента либо (для случая
то такая функция называется векторной функцией векторного аргумента либо (для случая  ) векторной функцией числового аргумента. Примеры отображений, которые не являются функциями, встречаются в геометрии. Например, любое преобразование плоскости – осевая или центральная симметрия, поворот на угол
) векторной функцией числового аргумента. Примеры отображений, которые не являются функциями, встречаются в геометрии. Например, любое преобразование плоскости – осевая или центральная симметрия, поворот на угол  вокруг центра, параллельный перенос и т.д.
вокруг центра, параллельный перенос и т.д.
Определение
Пусть задано отображение  . Полным прообразом элемента
. Полным прообразом элемента  при отображении
при отображении  называется множество всех
называется множество всех  таких, что
таких, что  . Для прообраза используется обозначение
. Для прообраза используется обозначение 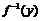 .
.
Определение
Пусть  . Отображение
. Отображение  будем называть инъективным отображением или вложением, если оно удовлетворяет условию:
будем называть инъективным отображением или вложением, если оно удовлетворяет условию: 

 - разным
- разным  сопоставлены разные элементы
сопоставлены разные элементы 
Иначе говоря, в прообраз каждого элемента множества  входит не более одного элемента
входит не более одного элемента  либо не входит ни один. Термин «вложение» подчёркивает тот факт, что инъективное отображение устанавливает взаимнооднозначное соответствие между множеством
либо не входит ни один. Термин «вложение» подчёркивает тот факт, что инъективное отображение устанавливает взаимнооднозначное соответствие между множеством  и некоторым подмножеством множества
и некоторым подмножеством множества 
Определение
Отображение  называется сюръективным или наложением, если
называется сюръективным или наложением, если 
Другими словами, если в отображении  каждый элемент
каждый элемент  имеет прообраз во множестве
имеет прообраз во множестве  т.е. во множестве
т.е. во множестве  нет «лишних» элементов.
нет «лишних» элементов.
Замечание. Отображение  есть отображение
есть отображение  на
на  , причём
, причём  Любое отображение можно сделать сюръективным, если вместо
Любое отображение можно сделать сюръективным, если вместо  рассматривать лишь его подмножество
рассматривать лишь его подмножество  :
: 
Определение
Отображение  называется биективным или взаимнооднозначным, если оно инъективно и сюръективно одновременно.
называется биективным или взаимнооднозначным, если оно инъективно и сюръективно одновременно.
Замечание. Рассмотрим функцию  . Если для
. Если для  уравнение
уравнение  имеет: а) не более одного решения, то функция инъективна; б) по крайней мере одно решение, то функция сюръективна; в) одно и только одно решение, то данная функция есть биекция.
имеет: а) не более одного решения, то функция инъективна; б) по крайней мере одно решение, то функция сюръективна; в) одно и только одно решение, то данная функция есть биекция.
Пример 1. Рассмотрим на плоскости круг  и прямую
и прямую  , а через
, а через  обозначим ортогональное проектирование круга на эту прямую. Является ли данное отображение инъективным, сюръективным или биективным?
обозначим ортогональное проектирование круга на эту прямую. Является ли данное отображение инъективным, сюръективным или биективным?

Данное отображение не является ни инъективным, ни сюръективным, ни биективным. Хотя для точек  и
и  прообраз содержит лишь один элемент, но для всех точек прямой
прообраз содержит лишь один элемент, но для всех точек прямой  , лежащих между
, лежащих между  и
и  , например, для точки
, например, для точки  , прообразом служит отрезок. Если же
, прообразом служит отрезок. Если же  , то прообраз
, то прообраз  есть пустое множество.
есть пустое множество.
Пример 2. Какая из указанных функций 
а)  ; б)
; б)  ; в)
; в) 
инъективна, сюръективна или биективна?
а) Для  уравнение
уравнение  имеет не более одного решения
имеет не более одного решения  , а именно, при
, а именно, при 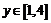 этим решением является
этим решением является 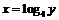 , а при
, а при  решений нет. Следовательно,
решений нет. Следовательно,  инъекция.
инъекция.
б) Для  уравнение
уравнение  имеет два решения:
имеет два решения:  и
и  , причём оба корня принадлежат
, причём оба корня принадлежат 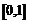 , совпадая при
, совпадая при  . Таким образом, данная функция сюръективна.
. Таким образом, данная функция сюръективна.
в) Для  уравнение
уравнение 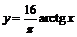 имеет единственное решение
имеет единственное решение  , принадлежащее отрезку
, принадлежащее отрезку 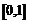 . Следовательно, функция
. Следовательно, функция  является биекцией.
является биекцией.
Существует несколько способов задания функции: аналитический способ, алгоритмический (посредством описания соответствия), табличный, графический, а также рекуррентное задание.
При аналитическом способе задаются формулы, использующие изученные ранее и специально обозначенные функции (например, 
 ), алгебраические действия, а также (как будет показано в курсе математического анализа) операцию предельного перехода.
), алгебраические действия, а также (как будет показано в курсе математического анализа) операцию предельного перехода.
Примерами функций, заданных с помощью описания, могут служить, например, функция  или функция Дирихле:
или функция Дирихле:  Здесь следует отметить, что всякая формула является символической записью некоторого описанного ранее соответствия (те же тригонометрические функции и т.д.), так что различие между заданием функции с помощью формулы или посредством описания является чисто внешним. Поэтому всякая вновь определённая функция, если ввести для неё специальное обозначение, может использоваться для определения других функций с помощью формул. Эти два способа задания функций являются наиболее важными для математического анализа.
Здесь следует отметить, что всякая формула является символической записью некоторого описанного ранее соответствия (те же тригонометрические функции и т.д.), так что различие между заданием функции с помощью формулы или посредством описания является чисто внешним. Поэтому всякая вновь определённая функция, если ввести для неё специальное обозначение, может использоваться для определения других функций с помощью формул. Эти два способа задания функций являются наиболее важными для математического анализа.
Табличный способ задания функции часто является следствием какого-либо эксперимента и особенно актуален в естественных науках и технике. Иногда данные таблиц могут быть получены и посредством математических расчётов.
Графическое задание функции осуществляется, например, с помощью самопишущих приборов (снятие кардиограммы) или на экране осциллографа. Следует отметить, что это задание приближённо.
Примером рекуррентного задания может служить следующая функция:  ,
,  ,
, 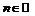 .
.
Определение сложной функции
Пусть  ,
,  . Композицией (суперпозицией, сложной функцией)
. Композицией (суперпозицией, сложной функцией)  называется отображение
называется отображение  в
в  , определённое формулой
, определённое формулой 

Отметим, что запись  производится в порядке, обратном тому, в котором производятся операции
производится в порядке, обратном тому, в котором производятся операции  и
и 
Пример 3. Пусть 

 ,
,  . Найти
. Найти 
Очевидно:  ,
, 
Пример 4. Найти 

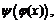
 если
если 

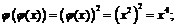
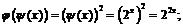
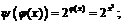

Пример 5. Найти 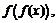
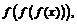 если
если 

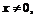



Определение обратной функции
Пусть отображение  есть биекция. Тогда отображение множества
есть биекция. Тогда отображение множества  на множество
на множество  , которое
, которое  ставит в соответствие
ставит в соответствие  такое, что
такое, что  , называется обратным отображением и обозначается
, называется обратным отображением и обозначается  .
.
Замечание. Если  есть биекция, то обратная биекция
есть биекция, то обратная биекция 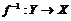 ставит в соответствие
ставит в соответствие  его единственный прообраз
его единственный прообраз 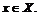 Таким образом,
Таким образом,

 ;
; 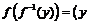
 .
.
Пример 6. Дана функция  . Найти
. Найти 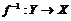 .
.
1) 
 ,
,  ,
,  , тогда
, тогда 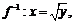


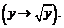
2) 


 , тогда
, тогда  ,
, 


Пример 7. Определить обратную функцию 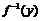 и её область существования, если
и её область существования, если 
На промежутке 
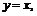 поэтому
поэтому 
 на отрезке
на отрезке 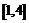
 при этом
при этом 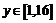 , следовательно, на сегменте
, следовательно, на сегменте 
 на промежутке
на промежутке 
 т.е.
т.е.  , поэтому
, поэтому 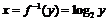 .
.
Таким образом, имеем следующую функцию, обратную заданной:

Основными или простейшими элементарными функциями являются:
1) степенная функция  ,
, 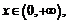


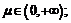
2) показательная функция 



3) логарифмическая функция 
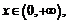


4) тригонометрические функции:












5) обратные тригонометрические функции:









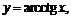


Для обратных тригонометрических функций имеют место следующие формулы:
1. 
 2.
2. 

3. 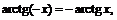
 4.
4. 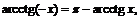

5. 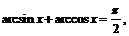
 6.
6. 

7. 

8. 

9. 
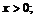
10. 

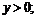
11. 

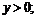
12. 


Докажем некоторые из них.
Например, нетрудно установить связь между  и
и  :
:
 или
или  (формулы 7 и 9).
(формулы 7 и 9).
Если положить  так что
так что  то
то  причём корень берётся со знаком «+», так как
причём корень берётся со знаком «+», так как  . Тогда
. Тогда  . Если же
. Если же  т.е.
т.е.  то
то 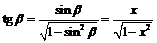 ,
, 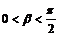 , откуда следует:
, откуда следует: 
Отметим, что, используя известные формулы для тригонометрических функций (теоремы сложения и т.д.), можно получить соответствующие теоремы и для обратных тригонометрических функций, нужно лишь внимательно следить за промежутками изменения аргументов.
Определение элементарной функции
Элементарной функцией называется функция, которая получается из основных элементарных функций с помощью четырёх арифметических действий и суперпозиций, последовательно примененных конечное число раз.
Например, функция 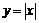 является элементарной:
является элементарной:  ; функция
; функция  также элементарна, а вот функция
также элементарна, а вот функция  согласно данному выше определению уже не является элементарной.
согласно данному выше определению уже не является элементарной.
Элементарные функции подразделятся на следующие классы.
1. Многочлены или полиномы, задаваемые формулами вида


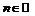 - степень полинома (целые функции).
- степень полинома (целые функции).
2. Рациональные функции (рациональные дроби), которые задаются в виде 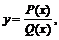 где
где 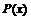 и
и  многочлены.
многочлены.
3. Алгебраические функции – функции, которые получаются с помощью суперпозиций рациональных функций, степенных функций с рациональными показателями и четырёх арифметических действий. Например,  .
.
Отметим, что класс многочленов содержится в классе рациональных функций, которые в свою очередь принадлежат классу алгебраических функций.
4. Трансцендентные функции – это функции, не являющиеся алгебраическими. Например, показательная, логарифмическая, тригонометрические и обратные тригонометрические функции являются трансцендентными.
Рассматривая функции, заданные формулой (или аналитически заданные), мы в первую очередь находим все те значения аргумента, при которых эта формула имеет смысл.
Пример 8. Найти область определения функции:
1)  2)
2) 
1) Из условия  находим:
находим: 
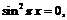

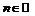 , откуда следует, что областью определения данной функции является:
, откуда следует, что областью определения данной функции является: 

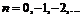 .
.
2) Функция  определена, если
определена, если  т.е.
т.е.  , а функция
, а функция  определена для всех
определена для всех  для которых
для которых  т.е. для
т.е. для  Следовательно, областью определения рассматриваемой функции является интервал
Следовательно, областью определения рассматриваемой функции является интервал 
При исследовании функций бывает также полезно установить такие свойства, как чётность либо нечётность, периодичность функции.
Пример 9. Определить, являются ли данные функции чётными либо нечётными, если:
1)  2)
2)  .
.
1) Данная функция является чётной, так как 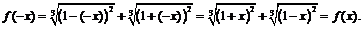
2) Функция  является нечётной:
является нечётной: 
Пример 10. Выяснить, являются ли данные функции периодическими, и определить наименьший период, если:
1)  2)
2)  .
.
1) Преобразуем данную функцию:
 Так как функция
Так как функция  является
является
 - периодической, то рассматриваемая функция
- периодической, то рассматриваемая функция
будет 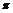 - периодической. Действительно,
- периодической. Действительно,

2) Найдём нули данной функции: 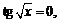 если
если 
 или
или 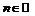 , т.е.
, т.е.  . Тогда расстояние между двумя соседними нулями при
. Тогда расстояние между двумя соседними нулями при  будет неограниченно возрастать:
будет неограниченно возрастать:
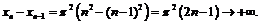 Следовательно, функция
Следовательно, функция  не является периодической.
не является периодической.
Упражнения для самостоятельной работы
Найти области определения следующих функций:
1.  2.
2. 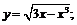 3.
3. 
4.  5.
5.  6.
6. 
7. а)  б)
б) 
8.  9.
9.  10.
10. 
11.  12.
12. 
13. 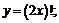 14.
14. 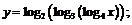 15.
15. 
16. 
 ; 17.
; 17. 
18. 19. 20..
21. Пусть функция 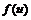 определена при
определена при  . Найти область определения функций: а)
. Найти область определения функций: а)  б)
б)  в)
в)  .
.
22. Пусть  . Определить
. Определить 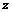 , если: а)
, если: а) 
б)  в)
в) 
 г)
г)  .
.
23. Найти  ,
,  ,
,  и
и  , если:
, если:
а)  ,
, 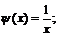 б)
б)  и
и 
24. Пусть  . Найти
. Найти  , если
, если 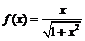 .
.
25. Найти 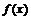 , если: а)
, если: а) 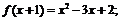 б)
б) 
в)  ,
,  г)
г) 
 .
.
26. Можно ли почленно логарифмировать неравенство?
27. Пусть 
 и
и 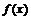 монотонно возрастающие функции. Доказать, что если
монотонно возрастающие функции. Доказать, что если  , то
, то  .
.
Определить обратную функцию и область её существования, если:
28. 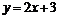 ,
,  29.
29.  , а)
, а) 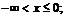 б)
б) 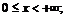
30.  ,
, 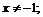 31.
31.  , а)
, а)  , б)
, б) 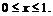
Определить, какие из функций являются чётными, а какие нечётными:
32. 33. 34..
Выяснить, какие из данных функций являются периодическими, и определить наименьший период их, если:
35.  36.
36. 
37.  38.
38.  39.
39. 
40.  41.
41.  42.
42.  .
.
43. Доказать, что для функции Дирихле  периодом является любое рациональное число.
периодом является любое рациональное число.
44. Доказать, что сумма и произведение двух периодических функций, которые определены на общем множестве и периоды которых соизмеримы, есть функции также периодические.
45. Функция 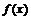 называется антипериодической, если
называется антипериодической, если 
 . Доказать, что
. Доказать, что 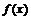 - периодическая функция с периодом
- периодическая функция с периодом 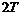 .
.
46. Доказать, что если для функции 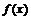
 выполнено равенство
выполнено равенство  , где
, где  и
и  - положительные постоянные, то
- положительные постоянные, то  , где
, где 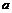 - постоянная, а
- постоянная, а  - периодическая функция с периодом
- периодическая функция с периодом  .
.






