Отношение эквивалентности. Связь между отношением эквивалентности и разбиением множества на классы

Определение. Отношение R на множестве X называется отношением эквивалентности, если оно рефлексивно, симметрично, транзитивно.

Эти условия можно записать «формулой»:

Примерами отношений эквивалентности являются: отношение равенства геометрических фигур, отношение подобия геометрических фигур, отношение параллельности прямых, отношение равносильности двух уравнений, отношения «быть однокурсником» на множестве студентов, «быть ровесником», «жить в одном доме» на множестве людей. На рис. 6 (из § 6 этой главы) графы I, IV, IX – это графы отношений эквивалентности.

В § 12 главы 1 мы рассмотрели разбиение множества на попарно непересекающиеся подмножества (классы), задавая свойства.

Всякое отношение эквивалентности осуществляет разбиение множества, в котором оно определено, на классы, обычно принимаемые за новые математические объекты, т.е. с помощью отношений эквивалентности порождаются новые математические объекты, понятия.

Так, например, отношение сонаправленности лучей разбивает множество всех лучей плоскости (пространства) на классы сонаправленных лучей (любые два луча одного класса сонаправлены, любые два луча различных классов не являются сонаправленными). Каждый из этих классов лучей называется направлением. Таким образом, интуитивное понятие направления получает точное математическое описание как класс разбиения множества лучей с помощью отношения эквивалентности.

О подобных фигурах обычно говорят, что они имеют одинаковую форму. Но что такое форма геометрической фигуры? Интуитивно ясно, что это то общее, что объединяет подобные фигуры. С помощью отношения эквивалентности удается это интуитивное понятие перевести в точное математическое. Отношение подобия, являясь отношением эквивалентности, разбивает множество фигур на классы подобных фигур. Каждый такой класс (эквивалентности) можно назвать формой. Тогда выражение: «Две подобные фигуры имеют одинаковую форму» имеет следующий точный смысл: «Две подобные фигуры принадлежат одной форме».

Отношения эквивалентности и осуществляемые ими разбиения множеств на классы встречаются не только в математике. Например, отношение «иметь один цвет» в множестве разноцветных фигур является отношением эквивалентности (легко заметить, что оно рефлексивно, симметрично и транзитивно). Полученные в результате решения задачи классы одноцветных фигур воспринимаются как новые понятие: красные, желтые, синие и т.д.

Представление о разбиении множества на классы введением в него отношения эквивалентности получает необходимое обоснование. Имеет место следующая теорема.

Теорема. Для того, чтобы отношение R позволяло разбить множество X на классы, необходимо и достаточно, чтобы R было отношением эквивалентности.

Доказательство.

Необходимость. Пусть задано разбиение множества X на классы. Покажем, что это разбиение позволяет определить в множестве X отношение эквивалентности. Зададим в множестве X отношение R указанием характеристического свойства: «элемент х находится в том же классе разбиения, что элемент у». Это отношение рефлексивно, поскольку всякий элемент х находится в одном классе с самим собой.

Далее, для любых элементов х и у из множества X из того, что х находится в том же классе что и у, следует, что у находится в том же классе что и х. Таким образом, отношение R симметрично. Кроме того, отношение R транзитивно, т.к. для любых трех элементов х, у, z из множества X справедливо следующее утверждение: если х находится в том же классе, что и у, а у – в том же классе что и z, то х находится в том же классе что и z. Итак, отношение R «находиться в одном и том же классе» рефлексивно, симметрично, транзитивно. Следовательно, R – отношение эквивалентности на множестве X.

Достаточность. Докажем теперь, что каждое отношение эквивалентности в множестве X определяет разбиение этого множества на попарно непересекающиеся подмножества (классы). Для этого поставим в соответствие каждому элементу а множества X его образ при отношении R, т.е. множество R (а) таких элементов х, что aRx. Так как отношение R рефлексивно, то для любого a Î Х имеем aRa, а это значит, что каждый элемент принадлежит соответствующему ему классу R (a), a Î R (a). Покажем, что если b Î R (a), то классы R (a) и R (b) совпадают. В самом деле, в этом случае имеем aRb. Если c Î R (b), то bRc, а из aRb и bRc в силу транзитивности имеем aRc. Но тогда c Î R (a). Значит, каждый элемент множества R (b) принадлежит R (a), т.е. R (b) Í R (a). Обратно, пусть c Î R (a), т.е. пусть aRc. Так как aRb, то в силу симметричности отношения R имеем bRa, а тогда из bRa и aRc следует, что bRc, и потому c Î R (b). Значит, любой элемент из R (a) принадлежит R (b), т.е. R (a) Í R (b). 

R (b) Í R (a) и R (a) Í R (b) Þ R (a) = R (b).

Из доказанного выше следует, что если множества R (a) и R (b) имеют хоть один общий элемент с, то они совпадают. В самом деле, в этом случае оба множества R (a) и R (b) совпадают с R (c), а потому и равны друг другу.

Таким образом, любые два множества R (a) и R (b) либо совпадают друг с другом (если b Î R (a)), либо не пересекаются друг с другом (если b Ï R (a)). А так как каждый элемент а принадлежит своему классу R (a), то мы получили разбиение X на попарно непересекающиеся подмножества (классы).

П р и м е р. Задайте все отношения эквивалентности на множестве X = {1, 2, 3} и нарисуйте их графы. Сколько их на множестве Х?

Решение. см. рис. 3, на котором изображено 5 графов.

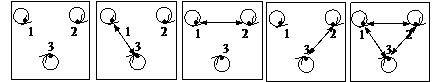Рис. 7