Модуль 2.
Лекция 17. Функция нескольких переменных
Раздел 17.1. n-мерное пространство
1. Многомерные пространства
2. Понятие расстояния (метрики). Метрическое пространство
3. Принципы кластерного анализа
Раздел 17.2 Функция нескольких переменных
1. Функция нескольких переменных
2. Частные производные
3. Двойной интеграл
4. Полярные координаты и интеграл Эйлера-Пуассона
Программные положения
В лекции рассматриваются вопросы, связанные с пространствами размерности больше двух: введение понятия расстояния, использования расстояния в кластерном анализе, функция нескольких (в нашем случае – двух) переменных, характеристика ее с помощью частных производных, а также вычисления площади и объема. Понятия функции двух переменных и двойного интеграла понадобятся нам при изучении случайных векторов в теории вероятностей. Завершается материал лекции вычислением интеграла Эйлера-Пуассона – одного из основных в теории вероятностей (неопределенный интеграл от функции Гаусса относится к неберущимся, а в случае наличия пределов интегрирования для вычисления подобных интегралов требуется применение неочевидных методов, один из которых и приводится здесь).
Методические рекомендации
Перед изучением материала лекции повторите определение функции, производной, интеграла.
Литература
Б.П.Демидович, В.А.Кудрявцев «Краткий курс высшей математики» Глава ХХ (§1, 2.3,10), Глава XXIV (§1, 2,3,4,7)
Вопросы для самоконтроля
1. Какое пространство называется n-мерным?
2. Каким условиям должно удовлетворять расстояние?
3. Какое пространство называется метрическим?
4. Для чего используется кластерный анализ?
5. Что представляет собой график функции 2 переменных? Что такое линии уровня?
6. Что такое частная производная?
7. Дайте определение двойного интеграла. Как с его помощью вычислить площадь и объем?
8. Найдите расстояние между точками А(1,2,3) и В(5,1,0) (используя разные расстояния)
9.Найти линии уровня функций
z = x + y.

10. Найти частные производные функции 
11.Найти площадь фигуры, ограниченной линиями
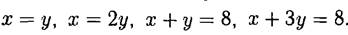
12. Вычислить

Раздел 17.1. Понятие многомерного пространства
Определение 17.1.1. n-мерного пространства.
Если на плоскости R2 фиксирована прямоугольная система координат, то между точками плоскости и всевозможными парами чисел (х, у) (х и у — координаты точек) существует взаимно однозначное соответствие. Если в пространстве задана аналогичная система координат, то между точками пространства и их координатами — всевозможными тройками (x,y,z) — также существует взаимно однозначное соответствие.
Расстояние (метрика). Метрическое пространство
Определение 17.1.2
Метрическое пространство (M, d) есть множество точек М, на квадрате которого (то есть для любой пары точек из М) задана функция расстояния (метрика). Она определяется следующим образом:
Для любых точек x, y, z из M эта функция должна удовлетворять следующим условиям:
- d (x, y) ≥ 0
- d (x, y) = 0
 x = y.
x = y. - d (x, y) = d (y, x) (симметрия)
- d (x, z) ≤ d (x, y) + d (y, z) неравенство треугольника (сумма двух сторон любого невырожденного треугольника всегда больше третьей стороны, в вырожденном случае имеет место равенство)
Эти аксиомы отражают интуитивное понятие расстояния. Например, расстояние должно быть неотрицательно и расстояние от x до y такое же, как и от y до x. Неравенство треугольника означает, что пройти от x до z можно короче, или хотя бы не длиннее, чем сначала пройти x до y, а потом от y до z.
Наиболее привычным для нас является евклидово расстояние. Однако, это далеко не единственный способ его задания. Например, будет удовлетворять вышеупомянутым аксиомам такое расстояние: d(x,y) = 1, если x ≠ y и d(x,y) = 0, если x = y.
В зависимости от конкретных нужд или свойств пространства можно рассматривать различные метрики.
Рассмотрим несколько примеров расстояний:
Определения 17.1.3.
Евклидово расстояние. Это, по-видимому, наиболее общий тип расстояния. Оно попросту является геометрическим расстоянием в многомерном пространстве и вычисляется следующим образом:
d(x,y) = {  i (xi - yi)2 }1/2
i (xi - yi)2 }1/2
Заметим, что евклидово расстояние (и его квадрат) вычисляется по исходным, а не по стандартизованным данным. Это обычный способ его вычисления, который имеет определенные преимущества (например, расстояние между двумя объектами не изменяется при введении в анализ нового объекта, который может оказаться выбросом). Тем не менее, на расстояния могут сильно влиять различия между осями, по координатам которых вычисляются эти расстояния. К примеру, если одна из осей измерена в сантиметрах, а вы потом переведете ее в миллиметры (умножая значения на 10), то окончательное евклидово расстояние (или квадрат евклидова расстояния), вычисляемое по координатам, сильно изменится, и, как следствие, результаты кластерного анализа могут сильно отличаться от предыдущих.
Квадрат евклидова расстояния. Стандартное евклидово расстояние возводят в квадрат, чтобы придать большие веса более отдаленным друг от друга объектам. Это расстояние вычисляется следующим образом (к нему также относится замечание о влиянии единиц измерения из предыдущего пункта):
d(x,y) =  i (xi - yi)2
i (xi - yi)2
Расстояние городских кварталов (манхэттенское расстояние). Это расстояние является просто средним разностей по координатам. В большинстве случаев эта мера расстояния приводит к таким же результатам, как и для обычного расстояния Евклида. Однако отметим, что для этой меры влияние отдельных больших разностей (выбросов) уменьшается (так как они не возводятся в квадрат). Манхэттенское расстояние вычисляется по формуле:
d(x,y) =  i |xi - yi|
i |xi - yi|
Расстояние Чебышева. Это расстояние может оказаться полезным, когда желают определить два объекта как "различные", если они различаются по какой-либо одной координате (каким-либо одним измерением). Расстояние Чебышева вычисляется по формуле:
d(x,y) = max |xi - yi|
(max означает максимум – наибольшее из всех значений модулей разностей)
Степенное расстояние. Иногда желают прогрессивно увеличить или уменьшить вес, относящийся к размерности, для которой соответствующие объекты сильно отличаются. Это может быть достигнуто с использованием степенного расстояния. Степенное расстояние вычисляется по формуле:
d(x,y) = ( i |xi - yi|p)1/r
i |xi - yi|p)1/r
где r и p - параметры, определяемые пользователем. Несколько примеров вычислений могут показать, как "работает" эта мера. Параметр p ответственен за постепенное взвешивание разностей по отдельным координатам, параметр r ответственен за прогрессивное взвешивание больших расстояний между объектами. Если оба параметра - r и p, равны двум, то это расстояние совпадает с расстоянием Евклида.






