Определение 17.1.4.
Кластерный анализ – это один из статистических методов, основывающихся не на идеях теории вероятностей, а на понятии расстояния.
Кластерный анализ решает задачу построения классификации, то есть разделения исходного множества объектов на группы (классы, кластеры). При этом предполагается, что у исследователя нет исходных допущений ни о составе классов, ни об их отличии друг от друга. Приступая к кластерному анализу, исследователь располагает лишь информацией о характеристиках (признаках) для объектов, позволяющей судить о сходстве (различии) объектов, либо только данными об их попарном сходстве (различии).
Например, задача обработки (классификации) массива данных – больных некоторой больницы. Каждому больному соответствует множество параметров (температура, давление, уровень гемоглобина крови и т.д.) и нам требуется разбить множество больных на группы.
Варианты кластерного анализа – это множество простых вычислительных процедур, используемых для классификации объектов. Классификация объектов – это группирование их в классы так, чтобы объекты в каждом классе были более похожи друг на друга, чем на объекты из других классов. Более точно, кластерный анализ – это процедура упорядочивания объектов в сравнительно однородные классы на основе попарного сравнения этих объектов по предварительно определенным и измеренным критериям.
Существует множество вариантов кластерного анализа, но наиболее широко используются методы, объединенные общим названием иерархический кластерный анализ (Hierarchical Cluster Analysis)
Кластерный анализ объектов, для которых заданы значения количественных признаков начинается с расчета различий для всех пар объектов. В качестве меры различия выбирается расстояние между объектами в Р-мерном пространстве признаков, чаще всего – евклидово расстояние или его квадрат
На первом шаге кластерного анализа путем перебора всех пар объектов определяется пара (или пары) наиболее близких объектов, которые объединяются в первичные кластеры. Далее на каждом шаге к каждому первичному кластеру присоединяется объект (кластер), который к нему ближе. Этот процесс повторяется до тех пор, пока все объекты не будут объединены в один кластер. Критерий объединения объектов (кластеров) может быть разным и определяется методом кластерного анализа. Основным результатом применения иерархического кластерного анализа является дендрограмма – графическое изображение последовательности объединения объектов в кластеры.
Есть методы с другой постановкой задачи. Например, вы можете указать желаемое количество кластеров с тем условием, чтобы они различались, как это только возможно (Метод К средних), или мы формулируем задачу деления на кластеры с «центрами» - характерными представителями каждой предполагаемой группы.
Можно указать ряд задач, при решении которых кластерный анализ является более эффективным, чем другие многомерные методы:
- разбиение совокупности испытуемых на группы по измеренным признакам с целью дальнейшей проверки причин межгрупповых различий по внешним критериям, например, проверка гипотез о том, проявляются ли типологические различия между испытуемыми по измеренным признакам;
- применение кластерного анализа как значительно более простого и наглядного аналога факторного анализа, когда ставится только задача группировки признаков на основе их корреляции;
- классификация объектов на основе непосредственных оценок различий между ними (например, исследование социальной структуры коллектива по данным социометрии – по выявленным межличностным предпочтениям).
Раздел 17.2. Функция нескольких переменных
Определение 17.2.1.
Пусть имеется n +1 переменная x 1, x 2,..., x n, y, которые связаны между собой так, что каждому набору числовых значений переменных x 1, x 2,..., xn соответствует единственное значение переменной y. Тогда говорят, что задана функция f от n переменных. Число y, поставленное в соответствие набору x 1, x 2,..., xn называется значением функции f в точке (x 1, x 2,..., xn), что записывается в виде формулы y = f (x 1 ,x 2,..., xn) или y =y (x 1 ,x 2,..., xn).
Переменные x 1, x 2,..., xn являются аргументами этой функции, а переменная y ‑ функцией от n переменных.
Далее будем говорить лишь о самом простом варианте - функции двух переменных. Для функций большего числа переменных все факты, о которых будет идти речь, или аналогичны или сохраняются без всякого изменения. Аргументы функции двух переменных будем обозначать как правило x и y, а значение функции z.
Определения 17.2.2.

|
Будем говорить, что задана функция двух переменных, если любой паре чисел (x,y) из некоторого множества D упорядоченных пар чисел поставлено в соответствие единственное число, которое обозначается f (x,y) и называется значением функции f в точке (x,y).
Множество D называется областью определения функции.
Поскольку любую пару чисел x,y можно рассматривать как пару координат точки M на плоскости, вместо z=f (x,y) можно писать z = f (M).При этом аргументами функции будут координаты x,y точки M.
Числа x, y можно рассматривать как координаты вектора  , исходящего из начала координат и с концом в точке M (x,y). Тогда функция двух переменных будет функцией вектора, что записывается в виде формулы z = f (
, исходящего из начала координат и с концом в точке M (x,y). Тогда функция двух переменных будет функцией вектора, что записывается в виде формулы z = f ( ), причем аргументами функции являются координаты вектора
), причем аргументами функции являются координаты вектора  .
.
График функции двух переменных есть множество точек (x, y, f (x, y)), где (x,y)Î D. График представляет собой некоторую поверхность. Пример такой
поверхности приводится на рисунке 1.
|
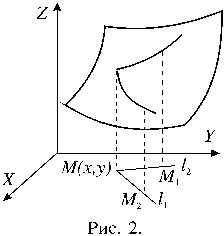
Очевидно, что нельзя ввести понятия возрастания или убывания (монотонности) функции двух переменных. Рассмотрим график некоторой функции z = f (x,y), изображенный на рисунке 2. Из точки M (x,y) в плоскости X,Y проведем два луча l 1 и l 2, определяющих некоторые направления. Можно говорить, что в точке M функция f в направлении l 1 возрастает, а в направлении l 2 убывает. Это означает, что для любой точки M 1, лежащей на луче l 1 достаточно близко к точке M, выполняется неравенство f (M 1) > f (M). Для любой точки M 2 , лежащей на луче l 2 достаточно близко к точке M, выполняется неравенство f (M 2) < f (M).
Одним из подходов к исследованию функций двух переменных является изучение поведения функции в точке, то есть определение направлений, в которых функция убывает или возрастает, и определение скорости возрастания или убывания.
Можно использовать другой подход. Пусть имеется функция z = f (x, y) c графиком, представляющим собой некоторую поверхность.
Определение 17.2.3.

|
Рассмотрим сечение графика функции плоскостью z=C (эта плоскость параллельна плоскости XOY и пересекает ось Z в точке z=C). Спроектируем линию пересечения этой плоскости с поверхностью z = f (x, y) на плоскость XOY и получим так называемую линию уровня C функции z = f (x, y). Линия уровня представляет собой множество всех точек в плоскости XOY, для которых выполняется равенство f (x, y) = C. Придавая различные значения параметру C, можно получить множество линий уровня функции f (x, y). Если для каждой линии уровня указать соответствующее ей значение C, то получится топографическая карта поверхности, представляющей собой график функции.
Пример 17.2.1.
Найти линии уровня функции 
Линия уровня z = с определяется уравнением  . Это
. Это
полупарабола, расположенная в первой четверти при с > 0, во
второй четверти плоскости Оху при с < 0, и полуось Оу (х = О,
у > 0), если с = 0.
Определения 17.2.4.
Пусть в плоскости XOY заданы две точки: M 0(x 0, y 0) и M 1(x 1, y 1). Расстояние r между этими точками, как мы уже говорили в разделе 17.1., в обычном евклидовом пространстве рассчитывается по формуле
 .
.
Пусть d ‑ некоторое положительное число. d -окрестностью Vd точки M 0(x 0, y 0) называется множество всех точек, координаты x,y которых удовлетворяют неравенствам
 .
.
Очевидно, что d -окрестность точки M 0(x 0, y 0) представляет собой круг радиуса d с выколотым центром (круг – множество точек, расстояние от которых до центра не больше радиуса)
Точка M 0(x 0, y 0) называется точкой минимума функции z = f (x, y), если существует такое положительное число d, что из условия M (x, y) Î Vd (x 0, y 0) следует f (x, y) > f (x 0, y 0).
Точка M 0(x 0, y 0) называется точкой максимума функции z = f (x, y), если существует такое положительное число d, что из условия M (x, y) Î Vd (x 0, y 0) следует: f (x, y) < f (x 0, y 0).
Точки минимума и максимума называются точками экстремума.
Число A называется пределом функции z = f (x, y) в точке M 0(x 0, y 0):
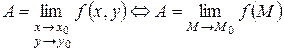 ,
,
если для произвольного числа e > 0 найдется такое число d > 0, что для всех точек M (x, y) из d -окрестности точки M 0(x 0, y 0) выполняется неравенство
| f (x, y) - A |< e.
Функция z = f (x, y)называется непрерывной в точке M 0(x 0, y 0), если
 .
.
Два последних определения фактически повторяют определения предела и непрерывности в точке для функции одной переменной.
Частные производные
Как мы показали ранее, производная функции (одной переменной) позволяет оценить скорость изменения ее значения. Но функция нескольких переменных может вести себя по-разному по каждой из переменных. Поэтому для этого случая невозможно ввести «определение вообще», а можно лишь дать
Определение 17.2.5.
Частной производной по x функции z = f (x, y) в точке M 0(x 0, y 0) называется предел

 ,
,
если этот предел существует. Обозначается эта частная производная любым из следующих символов (для производной по переменной х):
 ;
;  ;
;  .
.
Частная производная по x есть обычная производная от функции z = f (x, y), рассматриваемой как функция только от переменной x при фиксированном значении переменной y.
Совершенно аналогично можно определить частную производную по y функции z = f (x, y) в точке M 0(x 0, y 0):
 =
=  .
.

|
В пространстве XYZ условие y = y 0 описывает плоскость P, перпендикулярную оси OY и пересекающую эту ось в точке y 0. Плоскость P пересекается с графиком функции z = f (x, y), вдоль некоторой линии L, как показано на рисунке 1. Тангенс угла между плоскостью XOY и касательной к линии L в точке с координатами x 0, y 0 равен частной производной по x функции z = f (x, y)в этой точке. В этом состоит геометрический смысл частной производной.
Аналогичное заключение можно сделать относительно частной производной по y.
Примеры 17.2.1
Приведем примеры вычисления частных производных. Как говорилось выше, для вычисления частной производной по x функции z = f (x, y) нужно положить переменную y равной константе, а при нахождении частной производной по y нужно считать константой переменную x.
1.  .
.
2. 
Если частные производные функции z = f (x, y) существуют на некотором множестве, а точка, в которой вычисляются частные производные несущественна, то пользуются более короткими обозначениями:
 .
.
Сами частные производные могут являться функциями от нескольких переменных на некотором множестве. У этих функций тоже могут существовать частные производные по x и по y. Они называются вторыми частными производными или частными производными второго порядка и обозначаются zxx ¢¢, zyy¢¢, zxy¢¢ или  . Согласно определению
. Согласно определению  ;
;  . Последняя частная производная второго порядка называется смешанной. Смешанная частная производная второго порядка, вообще говоря, зависит от того, в какой последовательности берутся переменные, по которым вычисляется производная. Так, производная zxy¢¢ = (zx¢) y¢ может не быть равной zyx¢¢ = (zy¢) x¢.
. Последняя частная производная второго порядка называется смешанной. Смешанная частная производная второго порядка, вообще говоря, зависит от того, в какой последовательности берутся переменные, по которым вычисляется производная. Так, производная zxy¢¢ = (zx¢) y¢ может не быть равной zyx¢¢ = (zy¢) x¢.
Теорема 17.2.1. (без доказательства)
Если смешанные частные производные второго порядка непрерывны, то они не зависят от того, в какой последовательности вычислялись частные производные по x и по y. (Убедитесь в справедливости этой теоремы для функций, рассмотренных в приведенных выше примерах 1 и 2.)
Отметим очень важное отличие функции двух переменных от функции одной переменной. Из существования первых частных производных в точке не следует непрерывность функции в этой точке. Рассмотрим, например, функцию
 .
.
График этой функции во всех точках, не принадлежащих осям координат OX и OY, представляет собой плоскость, параллельную плоскости XOY, поднятую на 1. Сами эти оси координат также принадлежат графику рассматриваемой функции. Очевидно, что в точке (0,0) функция имеет частные производные по обоим аргументам, обе равные нулю. Очевидно также, что в любой окрестности точки (0,0) можно найти точку M такую, что f (M) = 1, в то время как f (0, 0) = 0. Это означает существование разрыва функции в точке (0,0).
Двойной интеграл
В области D плоскости Oxy определена непрерывная функция z = f(x,y). Область D разобьем каким-то образом на n элементарных областей (частей) D1, D2, D3, …, Dn. Через  обозначим площадь Dk (k=1,2,…,n), через dn – максимальный из диаметров областей Dk (под диаметром области будем понимать наибольшее расстояние между двумя ее точками) В каждой области Dk произвольно выберем по точке Mk (xk, yk) и составим интегральную сумму
обозначим площадь Dk (k=1,2,…,n), через dn – максимальный из диаметров областей Dk (под диаметром области будем понимать наибольшее расстояние между двумя ее точками) В каждой области Dk произвольно выберем по точке Mk (xk, yk) и составим интегральную сумму

Если f(x, y) ≥0, то слагаемое Mk (xk, yk)  обозначает объем цилиндра с основанием Dk и высотой f(Mk), а Vn – объем объединения всех таких цилиндров, то есть, примерный объем тела с основанием D, ограниченного цилиндрической поверхностью с образующей, параллельной оси Oz и поверхностью z = f(x,y) (см.рисунок ниже:)
обозначает объем цилиндра с основанием Dk и высотой f(Mk), а Vn – объем объединения всех таких цилиндров, то есть, примерный объем тела с основанием D, ограниченного цилиндрической поверхностью с образующей, параллельной оси Oz и поверхностью z = f(x,y) (см.рисунок ниже:)

Теорема 17.2.2.(без доказательства)
Если функция z =f(x,y) непрерывна в D, то при условии 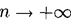 и
и 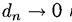
последовательность  имеет конченый предел
имеет конченый предел 
Определение 17.2. 6
Предел V называется двойным интегралом от функции f(x,y) по области D и обозначается 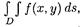 или
или  .
.
Из построения следует, что

Выражает площадь фигуры (области) D, а если f(x,y)≥0, то двойной интеграл
 выражает объем цилиндрического тела, «крыша» которого – поверхность z=f(x,y), а основание – область D.
выражает объем цилиндрического тела, «крыша» которого – поверхность z=f(x,y), а основание – область D.
Определение 17.2.7
Область D называется правильной относительно оси Oy (Ox), если каждая прямая, параллельная оси Oy (ox) и проходящая через внутреннюю точку, пересекает ее границу только в двух точках.
Нижняя (левая) из этих точек называется точкой входа в область, а нижняя (правая) – точкой выхода.
Область, правильную относительно обеих осей (направлений), называется правильной областью.
Такую область можно задать с помощью неравенств:
Для области, правильной относительно Oy


Для области, правильной относительно Oх



Определение 17.2.8
Интегралы, написанные справа от первого знака равенства, называются повторными. Двойной интеграл сводится таким образом к повторным. При вычислении внутреннего интеграла одна из переменных, дифференциал которой отсутствует, считается (временно) постоянной. В частности, если f(x,y) представима в виде g(x) ∙ h(x,y), то

Аналогично выносится множитель, зависящий только от у.
Примеры 17.2.2.
- Привести к повторному интеграл

Интеграл по области D, ограниченной кривыми

 Для области D можно записать:
Для области D можно записать: 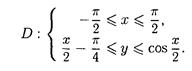

2. Найти площадь фигуры, ограниченной линиями 


3. Найти площадь фигуры, ограниченной линиями: 



4. Вычислить интеграл  где область D ограничена линиями
где область D ограничена линиями 
D = 







