Аксиомы действительных чисел
Множеством 
называется множество, на котором выполняются следующие условия:
Во множестве 
определена операция “сложение”: 
a. 
(сложение коммутативно);
b. 
(сложение ассоциативно);
с. 
(наличие нейтрального элемента);
d. 
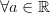
(наличие противоположного элемента).
Число 
называется разностью чисел 
и 
и 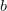обозначаются 
.
В определена операция “умножение”: 
а.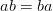 
(коммутативность умножения);
b. 
(ассоциативность умножения);
с. 
(наличие нейтрального элемента);
d. 
(наличие противоположного элемента).
– частное деление на 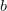и обозначается 
или 
.
Выполняется дистрибутивный закон (связь сложения и умножения):
.
либо 
, либо 
.
При этом, если и 
, 
.
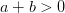Числа больше 0 называются положительными. Числа меньше 0 называются отрицательными.
Если 
, то пишут 
;
Если 
, то пишут 
;
Если 
, то пишут 
.
Для множеств:
Для 
Запись 
означает, что 
.
Если 
(множество из одного элемента) и , то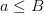 
.
Непрерывность множества заключается в том, что в нет “щелей”, а именно справедлива:
Аксиома непрерывности
.
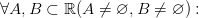
Неравенство Бернулли
Пусть 
. Тогда
Доказательство:
Если n=1 неравенство очевидно. Допустим, оно выполняется при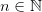 
. Докажем его справедливость при 
. Действительно:
;
.
Что и требовалось доказать. 
Аксиома полноты или непрерывности множества веще- ственных чисел состоит в следующем. Если X и Y — непустые подмножества R, обладающие тем свой- ством, что для любых элементов x ∈ X и y ∈ Y выполнено x ≤ y, то существует такое c ∈ R, что x ≤ c ≤ y для любых элементов x ∈ X и y ∈ Y. Этим завершается список аксиом, выполнение которых на каком бы то ни было множестве R позволяет считать это множество кон- кретной реализацией или, как говорят, моделью действительных чисел
Аксиома непрерывности
Следующее предложение представляет собой, пожалуй, наиболее простую и удобную для приложений формулировку свойства непрерывности действительных чисел. При аксиоматическом построении теории действительного числа данное утверждение, или эквивалентное ему, непременно входит в число аксиом действительного числа [3].
Геометрическая иллюстрация аксиомы непрерывности
Каковы бы ни были непустые множества {\displaystyle A\subset \mathbb {R} } и {\displaystyle B\subset \mathbb {R} }, такие что для любых двух элементов {\displaystyle a\in A} и {\displaystyle b\in B} выполняется неравенство {\displaystyle a\leqslant b}, существует такое действительное число {\displaystyle \xi }, что для всех {\displaystyle a\in A} и {\displaystyle b\in B} имеет место соотношени {\displaystyle a\leqslant \xi \leqslant b}
Геометрически, если трактовать действительные числа как точки на прямой, данное утверждение представляется очевидным. Если два множества {\displaystyle A} и {\displaystyle B} таковы, что на числовой прямой все элементы одного из них лежат левее всех элементов второго, то найдется число {\displaystyle \xi }, разделяющее эти два множества, то есть лежащее правее всех элементов {\displaystyle A} (кроме, возможно, самого {\displaystyle \xi }) и левее всех элементов {\displaystyle B} (та же оговорка).
Здесь следует отметить, что несмотря на «очевидность» данного свойства, для рациональных чисел оно не всегда выполняется.
Роль аксиомы непрерывности в построении математического анализа
Значение аксиомы непрерывности таково, что без неё невозможно строгое построение математического анализа.[ источник не указан 1856 дней ] Для иллюстрации приведем несколько фундаментальных утверждений анализа, доказательство которых опирается на непрерывность действительных чисел:
· (Теорема Вейерштрасса). Всякая ограниченная монотонно возрастающая последовательность сходится
· (Теорема Больцано — Коши). Непрерывная на отрезке функция, принимающая на его концах значения разного знака, обращается в нуль в некоторой внутренней точке отрезка
· (Существование степенной, показательной, логарифмической и всех тригонометрических функций на всей «естественной» области определения). Например, доказывается, что для всякого {\displaystyle a>0} и целого {\displaystyle n\geqslant 1} существует {\displaystyle {\sqrt[{n}]{a}}}, то есть решение уравнения {\displaystyle x^{n}=a,x>0}.
19. Предел монотонной ограниченной последовательности.
Теорема Вейерштрасса
Теорема
Теорема Вейерштрасса. (Основная теорема теории последовательностей).
Если последовательность 
является нестрого возрастающей (нестрого убывающей) и ограничена сверху (снизу), то является сходящейся.
Данную теорему можно сформулировать немного иначе - Любая монотонная и ограниченная последовательность имеет предел.
Для того чтобы монотонная последовательность сходилась, достаточно, чтобы она была ограниченной.
Замечание
Если последовательность монотонная, то для того, чтобы она была сходящейся, необходимо и достаточно, чтобы она была ограниченной.
Число е (число Эйлера)
Используя теорему Вейерштрасса, можно показать, что последовательность 
является сходящейся, то есть имеет предел. Данный предел равен числу е - числу Эйлера, которое является основанием натурального логарифма:
| 20. Теорема (Бенулли, неравенство): |
light:  hard: 
|
20. Теорема Кантора
В теории множеств теорема Кантора гласит, что
| Любое множество менее мощно, чем множество всех его подмножеств. |
21. Второй замечательный предел
Второй замечательный предел:
здесь е - число Эйлера. является основанием натурального логарифма.
Число e, второй замечательный предел
Числом e называется предел
Это число иррациональное и приближенно равно е = 2.718281828.... Логарифмы с основанием е называются натуральными и обозначаются
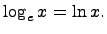
Данный предел называют вторым замечательным пределом.
Число е
Рассмотрим числ. посл-ть с общим членом xn=(1+1/n)^n (в степени n)(1).
Оказывается, что посл-ть (1) монотонно возр-ет, ограничена сверху и сл-но
явл-ся сходящейся, предел этой пос-ти наз-ся экспонентой и обозначается
символом е»2,7128.
23. Непрерывная функция — функция без «скачков», то есть такая, у которой малые изменения аргумента приводят к малым изменениям значения функции.
| 23. Свойства непрерывных функций | ||
Теорема 1. Сумма непрерывных функций есть функция непрерывная. Доказательство. Пусть функции  и  непрерывны в точке a. Тогда
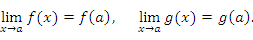Согласно свойству пределов функций существование пределов функций и гарантирует существование предела их суммы. При этом
что и требовалось доказать. Свойство. Сумма конечного числа непрерывных функций есть функция непрерывная. Доказательство. Каждую пару непрерывных функций можно заменить одной непрерывной функцией. Затем каждую пару полученных непрерывных функций можно заменить одной непрерывной функцией. В конечном итоге останется одна непрерывная функция.
Теорема 2. Произведение непрерывных функций есть функция непрерывная. Свойство. Произведение конечного числа непрерывных функций есть функция непрерывная. Теорема 3. Частное от деления непрерывных функций есть функция непрерывная – за исключением точек, в которых знаменатель обращается в нуль. Доказательство теорем 2 и 3 по своей сути не отличается от доказательства теоремы 1 и предоставляется читателю.
Теорема 4. Любая элементарная функция непрерывна в области своего определения. Для доказательства этой теоремы нужно показать, что для любого числа a из области определения элементарной функции выполняется условие
Продемонстрируем справедливость теоремы на некоторых конкретных примерах.
1. Пусть  , где n – целое положительное число. Тогда
 
Первый член в правой части этого равенства представляет собой бесконечно малую функцию при x → a и, следовательно,
2. Покажем, что показательная функция  является непрерывной в каждой точке a. Действительно,
  
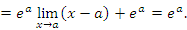Теорема 5. Пусть функция непрерывна на промежутке [ a, b ] и принимает на его концах значения разных знаков. Тогда на этом промежутке существует такая точка c, в которой  . Действительно, непрерывность функции на некотором промежутке означает отсутствие скачков функции на этом промежутке. Другими словами, принимает все значения, заключенные между ее минимальным и максимальным значениями на промежутке [ a, b ], одним из которых является нулевое значение. Отметим, что теорема 5 лежит в основе численных методов решения уравнений.
| ||
