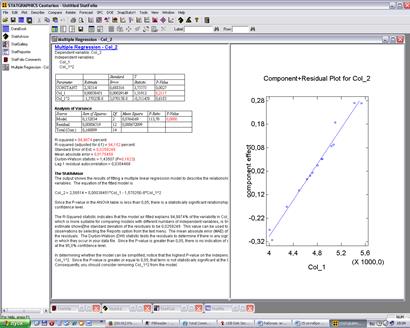
Характер расположения точек на диаграмме рассеяния позволяет сделать предположение о параболической регрессионной зависимости
.
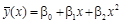Оценки параметров b0 , b1 и b2 найдем методом наименьших квадратов. Для этого составим функцию S (b0 , b1 , b2), которая в случае параболической регрессии примет вид
.
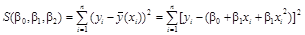Для отыскания оценок параметров b0 , b1 и b2, минимизирующих функцию S (b0 , b1 , b2), составим и решим систему нормальных уравнений:
Þ 
Þ
Разделим обе части уравнений (1,2,3) на (-2):
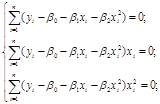Þ 
ÞÞ 
Þ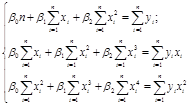 
Для вычисления значений сумм, входящих в систему уравнений, составим расчетную таблицу 4.4.
После подстановки значений система уравнений примет вид:
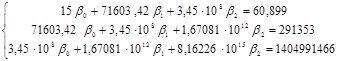
Таблица 4.4 – Результаты промежуточных вычислений
Вес грузового состава, т,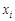 
| Время нахождения поезда на участке, час., 
| 
| 
| 
| 
| 
|
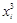
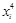
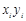
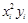
| 5100,58 | 4,2 | 1,33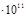 
| 6,77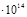 
| 21422,44 | 109266848,6 | |
| 4885,41 | 4,078 | 1,17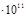
| 5,70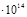
| 19922,70 | 97330567,48 | |
| 5416,94 | 4,23 | 1,59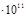
| 8,61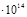
| 22913,66 | 124121900,8 | |
| 4496,66 | 4,001 | 0,91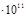
| 4,09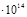
| 17991,14 | 80900024,57 | |
| 4722,08 | 4,044 | 1,05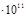
| 4,97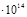
| 19096,09 | 90173271,84 | |
| 5537,91 | 4,208 | 1,70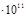
| 9,41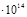
| 23303,53 | 129052825,7 | |
| 5074,01 | 4,11 | 1,31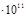
| 6,63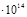
| 20854,18 | 105814323,4 | |
| 4807,09 | 4,062 | 1,11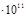
| 5,34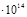
| 19526,4 | 93865160,16 | |
| 4046,02 | 3,85 | 0,66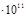
| 2,68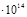
| 15577,18 | 63025569,69 | |
| 4683,93 | 4,037 | 1,03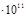
| 4,81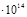
| 18909,03 | 88568551,39 | |
| 4872,42 | 4,08 | 1,16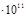
| 5,64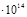
| 19879,47 | 96861144,76 | |
| 4003,22 | 3,9 | 0,64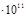
| 2,57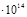
| 15612,56 | 62500504,44 | |
| 4628,01 | 4,03 | 0,99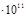
| 4,59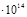
| 18650,88 | 86316460,54 | |
| 4293,44 | 3,96 | 079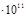
| 3,40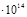
| 17002,02 | 72997163,05 | |
| 5035,7 | 4,109 | 1,28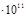
| 6,43 | 20691,69 | 104197149,9 | |
| Итого 71603,42 | 60,899 | 3,45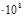 
| 1,67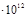 
| 8,16 
| 291353,0 | 1404991466,0 |
Решив систему уравнений известными методами (методом Крамера, методом Гаусса, методом обратной матрицы) или с помощью MAthCAD, получим следующее решение: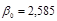 
; 
; 
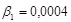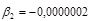, а уравнение регрессии примет вид
.
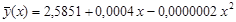На рисунке представлена диаграмма рассеяния случайных величин X и Y с нанесённой линией регрессии.
Рисунок 4.4 – Диаграмма рассеяния случайных величин X и Y с нанесённой линией регрессии
Оценим качество описания зависимости между величиной временем нахождения поезда на участке (Y) и весом грузового состава (Х) полученным уравнением регрессии с помощью коэффициента детерминации, где
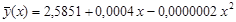– значение времени нахождения поезда на участке, предсказываемое уравнением регрессии, при среднем весе грузового состава xi;
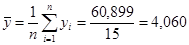час. – среднеарифметическое наблюденных значений времени нахождения поезда на участке.
Таблица 4.6 – Значения времени нахождения поезда на участке
| Вес грузового состава, т,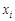
| Время нахождения поезда на участке, час.,
| Значение, предсказываемое уравнением регрессии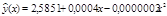 
| 
| 
|
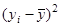
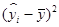
| 5100,58 | 4,2 | 4,105 | 0,0196 | 0,00203 |
| 4885,41 | 4,078 | 4,0619 | 0,0003 | 3,9E-06 |
| 5416,94 | 4,23 | 4,165 | 0,0289 | 0,01104 |
| 4496,66 | 4,001 | 3,9794 | 0,0035 | 0,00649 |
| 4722,08 | 4,044 | 4,028 | 0,0003 | 0,00102 |
| 5537,91 | 4,208 | 4,1869 | 0,0219 | 0,01612 |
| 5074,01 | 4,11 | 4,0998 | 0,0025 | 0,00159 |
| 4807,09 | 4,062 | 4,0458 | 4E-06 | 0,0002 |
| 4046,02 | 3,85 | 3,8761 | 0,0441 | 0,03379 |
| 4683,93 | 4,037 | 4,0199 | 0,0005 | 0,0016 |
| 4872,42 | 4,08 | 4,0593 | 0,0004 | 4,6E-07 |
| 4003,22 | 3,9 | 3,8659 | 0,0256 | 0,03766 |
| 4628,01 | 4,03 | 4,0079 | 0,0009 | 0,0027 |
| 4293,44 | 3,96 | 3,9338 | 0,01 | 0,01591 |
| 5035,7 | 4,109 | 4,0922 | 0,0024 | 0,00104 |
| Итого 71603,42 | 60,899 | 60,527 | 0,1609 | 0,152839 |
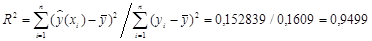
Расчётное значение коэффициента детерминации 
указывает на удовлетворительность описания зависимости между величиной веса грузового состава (Х) и времени нахождения поезда на участке (Y), выбранным уравнением регрессии. Проверим, однако, значимость оценки коэффициента детерминации с помощью статистики Фишера.
Проверка значимости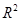 
. При выполнении процедуры проверки значимости оценки коэффициента детерминации выдвигается нулевая гипотеза о том, что предложенное уравнение регрессии никак не отражает реальную зависимость между с. в., т. е. H 0: R 2 = 0. Альтернативная гипотеза заключается в том, что выбранная модель зависимости (уравнение регрессии) 
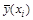в достаточной степени объясняет действительную зависимость между случайными величинами, т. е. H a: R 2 > 0.
Для проверки значимости оценки коэффициента детерминации используем статистику
,
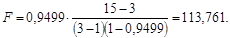
Вывод. Критическое значение статистики Фишера для степеней свободы n1 = 3 – 1 = 2 и n2 = 15 – 3 = 12 и уровня значимости a = 0,05 составляет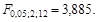 
(Приложение Б). Поскольку расчётное значение статистики Фишера больше критического (
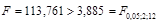), то вычисленный коэффициент детерминации значимо отличается от нуля, и выбранное уравнение регрессионной зависимости между величинами скорости и временем нахождения поезда на участке.
Например, при весе грузового состава 6500 т можно ожидать в среднем время нахождения поезда на участке 
час.
