· Значения коэффициента в нижеследующих формулах:
· Угол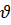 
на которой рассеивается заряженная частица кулоновским полем неподвижного ядра определяется формулой:
Где 
- заряды частицы, b – прицельный параметр, Т-кинетичесая энергия налетающей частицы.
· Формула Резерфорда. Относительное число частиц, рассеянных в элементарном телесном угле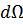 
под углом 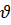к первоначальному направлению их движения:
Где n – число ядер фольги на единицу ее поверхности, 
· Обобщенная формула Бальмера:
Где 
– частота перехода между энергетическими уровнями с квантовыми числами n1 и n2, R,c-1 – постоянная Ридберга, Z – порядковый номер водородоподобного иона. Рис 6.1 – схема соответствующих переходов.
6.29. Излучение атомарного водорода падает нормально на дифракционную решетку ширины 
. В наблюдаемом спектре под некоторым углом дифракции 
оказалась на пределе разрешения (по критерию Рэлея) 50-я линия серии Бальмера. Найти этот угол
6.30. Какому элементу принадлежит водородоподобный спектр, длины волн линий которого в четыре раза короче, чем у атомарного водорода?
6.31. Сколько спектральных линий будет испускать атомарный водород, который возбуждают на n-й энергетический уровень?
6.32. Какие линии содержит спектр поглощения атомарного водорода в диапазоне длин волн от 94,5 до 130,0 нм?
6.33. Найти квантовое число n, соответствующее возбужденному состоянию иона He+, если при переходе в основное состояние этот ион испустил последовательно два фотона с длинами волн 108,5 и 30,4 нм.
6.34. Вычислить постоянную Ридберга R, если известно, что для ионов He+ разность длин волн между головными линиями серий Бальмера и ЛайманаΔλ = 133,7 пм.
6.35. У какого водородоподобного иона разность длин волн между головными линиями серий Бальмера и Лаймана равна 59.3 нм?
6.43. Покоящийся ион Не+ испустил фотон, соответствующий головной линии серии Лаймана. Этот фотон вырвал фотоэлектрон из покоящегося атома водорода, который находился в основном состоянии. Найти скорость фотоэлектрона.
6.44. Найти скорость возбужденных атомов водорода, если при наблюдении их излучения под углом 
к направлению движения данных атомов длина волны головной линии серии Лаймана оказалось смещенной на 
6.45. Согласно постулату Бора-Зоммерфельда при периодическом движении частицы в потенциальном поле должно выполняться следующее правило квантования: 
, где q и p – обобщенные координата и импульс, n – целые числа. Воспользовавшись этим правилом, найти разрешенные значения энергии частицы массы m, которая движется:
a) в одномерной прямоугольной потенциальной яме ширины l c бесконечно высокими стенками;
b) по окружности радиуса r;
c) в одномерном потенциальном поле 
положительная постоянная;
d) по круговой орбите в центральном поле, где потенциальная энергия частицы поле 
- положительная постоянная;
6.46. Найти с учетом движения ядра атома водорода выражения для энергии связи электрона в основном состоянии и для постоянной Ридберга. На сколько процентов отличаются энергия связи и постоянная Ридберга, полученные без учета движения ядра, от соответствующих уточненных значений этих величин?
6.47.Найти для атомов легкого и тяжелого водорода (H и D) разность:
a) энергии связи их электронов в основном состоянии;
b) длин волн головных линий серии Лаймана;
6.48. Вычислить расстояние между частицами системы в основном состоянии, соответствующую энергию связи и длину волны головной линии серии Лаймана, если системой является:
a) мезоатом водорода, ядром которого служит протон(в мезоатоме вместо электрона движется мезон, имеющий тот же заряд, но массу в 207 раз большую);
b) позитроний, который состоит из электрона, движущихся вокруг общего центра масс.
Волновые свойства частиц
· Дебройлевская длина волны частицы с импульсом p:
· Соотношение неопределенностей:
· Временное и стационарное уравнения Шредингера:
(6.2 в)
где 
–полная волновая функция, 
- ее координатная часть, 
- оператор Лапласа, E и U- полная и потенциальная энергия частицы. В сферических координатах:
· Среднее значение величины q, являющейся функцией координат:
где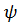 
–нормированная волновая функция, dV- элемент объема.
· Коэффициент прозрачности потенциального барьера U(x):
Где – x1 и x2 координаты точек, между которыми U>E.
6.78 Поток электронов падает на экран с двумя щелями 1 и 2(рис 6.3).В точке Р расположено входное отверстие счетчика. Пусть 
– амплитуда волны, прошедшей через щель 1 и достигшей Р, а 
– то же, но в случае открытой щели 2, Отношение 
.Если открыта только щель 1, то счетчик регистрирует 
электронов в секунду. Сколько электронов ежесекундно будет регистрировать счетчик, если:
1. открыта только щель 2;
2. открыты обе щели и в точке Рнаблюдаеться интерференционный максимум;
3. То же, но в точке Р-минимум?
6.79 Найти частное решение временного уравнения Шрёдингера для свободного движущейся частицы массы m.
6.80 Электрон находиться в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками. Найти ширину ямы, если разность энергии между уровнями с 
=2 
=3 составляет 
6.81 Частица находиться в основном состоянии в одномерной прямоугольной потенциальной яме ширины 
с абсолютно непроницаемыми стенками 
. Найти вероятность пребывания частицы в области 
6.82Частица находится в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками. Ширина ямы . Найти нормированные волновые функции стационарных состояний частицы, взяв начало отсчета координаты х в середине ямы.
6.83 В момент 
волновая функция некоторой частицы имеет вид 
. Изобразить примерный вид зависимостей:
1. Действительной части 
2. 
6.84Электрон находится в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками. Ширина ямы такова, что энергетические уровни расположены весьма густо. Найти плотность уровней 
,т.е их число на единичный интервал энергии, в зависимости от 
. Вычислить 
для 
, если 
6.85 Частица массы mнаходиться в двумерной прямоугольной потенциальной яме с абсолютно непроницаемыми стенками. Найти:
1. Возможные значения энергии частицы, если стороны ямы равны 
2. Значения энергии частицы на первых четырех уровнях, если яма квадратная со стороны 
6.94. Частица массы m находится в сферически – симметричной потенциальной яме U(r)=0 при r<r0 и U(r)=U0 при r>r0
a) Найти с помощью подстановки 
уравнение определяющее собственные значения энергии Е частицы при E<U0, когда движение описывается волновой функцией 
, зависящей только от 
. Привести это уравнение к виду
где 
b) Определить значение величины 
, при котором появляется первый уровень.
6.95.Волновая функция частицы массы m для основного состояния в одномерном потенциальном поле 
имеет вид 
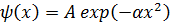, где А и 
– некоторые постоянные. Найти с помощью уравнения Шредингера постоянную и энергию Е частицы в этом состоянии.
6.96. Определить энергию электрона атома водорода в состоянии, для которого волновая функция имеет вид 
, где А, a и – некоторые постоянные.
6.97. Волновая функция электрона в основном состоянии атома водорода имеет вид 
, где А – некоторая постоянная, 
- первый Боровский радиус. Найти:
a) Наиболее вероятное расстояние между электроном и ядром;
b) Среднее значение модуля кулоновской силы, действующий на электрон;
c) Среднее значение потенциальной энергии электрона в поле ядра.
6.98. Частица находится в сферически-симметричном потенциальном поле в стационарном состоянии 
, где r – расстояние от центра поля. Найти <r>.
6.99. Частица массы m находится в одномерном потенциальном поле 
, где 
- положительная постоянная. Найти <U> частицы в состоянии, описываемом волновой функцией 
, где А и – неизвестные постоянные.
6.100. Частица в момент t=0 находится в состоянии 
, где А и – некоторые постоянные. Найти:
a) <x>; б) <px> - среднее значение проекции импульса.
6.101. Найти средний электростатический потенциал импульса, создаваемый электроном в центре атома водорода, если электрон находится в основном состоянии, для которого волновая функция , где А – некоторая постоянная, - первый Боровский радиус.
6.103 Воспользовавшись формулой 
, найти для электрона с энергией 
вероятность 
прохождения потенциального барьера, ширина которого 
и высота 
, если барьер имеет форму, показанную:
1. На рис. 6.7
2. На рис. 6.8
