Задача 4 (описанный четырехугольник).

В равнобедренную трапецию АВСD с основаниями AD и ВС вписана окружность, СН – высота трапеции.

а) Доказать, что центр окружности, вписанной в трапецию, лежит на отрезке ВН.

K

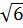б) Найдите диагональ АС, если известно, что средняя линия трапеции равна , а угол AOD равен 135°, где О – центр окружности, вписанной в трапецию, AD – большее основание.

Решение.

 

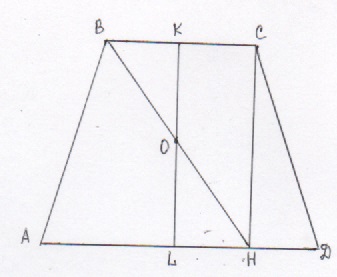
а) 1) Пусть точки K и L – точки касания окружности оснований трапеции, тогда

ОК = ОL = r_впис

2) ΔBOK=ΔHOL по катету(см. пункт 1) и острому углу (углы OBK и LHO равны как накрест лежащие при BC II AD и секущей BH. Поэтому ВО = ОН.

3) Центр вписанной в трапецию окружности лежит на пересечении биссектрис внутренних углов трапеции. Данная трапеция ABCD – равнобедренная, поэтому углы ОВК и ОСК равны. Значит, треугольники ΔВОК и ΔСОК равны (по катету и острому углу)

4) Из 2) и 3) следует, что ВО=ОС=ОН. Точка О равноудалена от вершин прямоугольного треугольника ΔВСН. О – центр описанной около треугольника окружности. Следовательно О принадлежит ВН (его середина). Пункт а) доказан.

б) Для доказательства пункта б) сделаем дополнительный чертеж

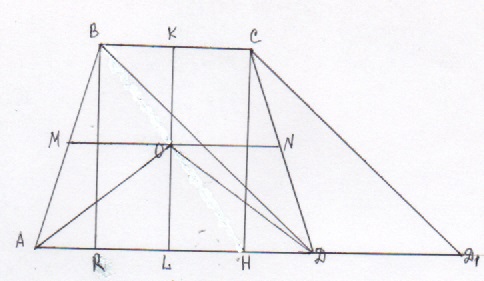
1) Пусть MN – средняя линия трапеции. Точка О принадлежит MN и О – её середина, поэтому МО =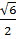

2) АО – биссектриса, углы МАО и RAO равны, углы RAO и МОА раны как накрест лежащие. ΔАМО – равнобедренный, АМ=МО= 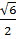. Тогда АВ = 2АМ=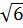

3) ∠AOD=135° (по условию), ∠OAD+∠ODA=45°. Значит, ∠BAD=∠CDA=45°. Пусть BR перпендикулярен AD. BR = AR=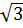

4) Пусть CD₁ II BD и точка D₁ лежит на прямой AD. Четырехугольник ВСD₁D – параллелограмм. CD₁=BD (противоположные стороны), BD=AC(диагонали равнобедренной трапеции). Тогда СD₁=BD=AC.

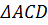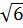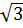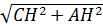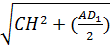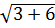5) ₁ – равнобедренный, AD₁ – основание. АD₁=AD+DD₁=AD+BC=2MN=2 . CH=BR= . По теореме Пифагора из ΔCHА: AC= = ²= = 3

Ответ: АС = 3.

 

Задача 5

В треугольнике АВС угол ВАС равен 60^°, угол АВС равен 45^°. Продолжения высот треугольника АВС пересекают описанную около него окружность в точках M, N, P.

а) Докажите, что треугольник MNP прямоугольный.

б) Найдите площадь треугольника MNP, если ВС=12.

Повторить. Свойство вписанных углов; теорему синусов.

Решение.

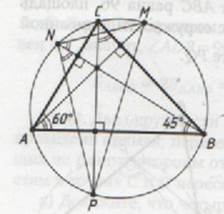а) Пусть продолжения высот треугольника АВС, проведенных из вершин А, В и С, пересекают описанную около него окружность в точках M, N и P соответственно.

Тогда вписанные углы PNB и PCB опираются на одну и ту же дугу, поэтому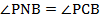

Аналогично,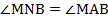

Значит,

 

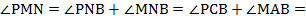
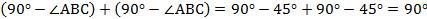
Следовательно, треугольник MNP прямоугольный. Пункт а) доказан.

б) Угол MNA равен углу NBA, угол APM равен углу ACP (вписанные углы, опирающиеся на одну дугу).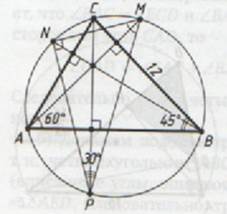

Тогда

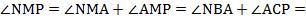
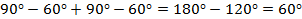
Следовательно, 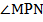= 30^°.

Пусть R – радиус описанной окружности треугольника АВС. По теореме синусов

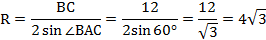
Тогда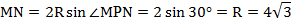

=

 

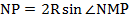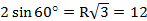
Следовательно,
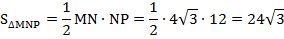Ответ: