Нерівнорозподіленим (несиметричним) називають навантаження при якому в кожну фазу ввімкнені споживачі, які відрізняються між собою за величиною або характером (фізичним змістом). Тобто, коли Z a ¹ Z в ¹ Z c.
У випадку (рис. 3.7), коли до джерела симетричної трифазної напруги U л підключені споживачі Z a ¹ Z в ¹ Z c (Y а ¹ Y в ¹ Y c),з’єднані у зірку, між нейтральними точками джерела і споживача виникає вузлова напруга – напруга зміщення нейтрали 
і, таким чином, у нейтральному проводі діє струм 
. Зв’язок між цими величинами можна показати на підставі закону Ома або другого закону Кірхгофа:
.
З рівнянь випливає, що основними факторами, які визначають чисельні значення 
та 
є опір Z N (провідність Y N = 1 / Z N) нейтрального проводу та ступінь нерівномірності навантажень у фазах споживача. Практично тут можуть мати місце такі варіанти:
1. Чотирипровідна зірка, де Z N = 0, тобто Y N = ¥;
2. Чотирипровідна зірка, де 0 < Z N < ¥, тобто Y N ¹ 0;
3. Трипровідна зірка, де Z N = ¥, тобто Y N = 0.
Відмітимо, що при нерівнорозподіленому навантаженні у фазах споживача розрахунок з’єднання потрібно виконувати окремо для кожної з його фаз і що зручніше це робити символічним методом.
За наведеною у попередньому розділі структурою розглянемо визначені варіанти.
Для чотирипровідної зірки, коли Z a ¹ Z в ¹ Z c (Y а ¹ Y в ¹ Y c)та Z N =0 (Y N = ¥), зазначимо, що при цьому відбувається незалежна робота фаз. З рівняння розрахунку напруги зміщення нейтралі випливає, що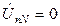 
. Це означає, що фазні напруги споживача дорівнюють відповідним фазним напругам джерела і, отже, для споживача виконується співвідношення 
. Тому, розрахувавши модуль фазної напруги джерела –
,
який в силу умов, що: UAB = UBC = UCA = Uaв = Uвc = Uca та UNn = 0, дорівнює модулю фазної напруги споживача, і записавши значення комплексів цих напруг (прийнявши початкові умови):
;
;
.
За методикою розрахунку кола однофазного синусоїдного струму виконаємо розрахунок кожної фази з’єднання окремо.
Лінійні, вони ж фазні, струми джерела і споживача визначають за законом Ома, а струм у нейтральному проводі - за першим законом Кірхгофа:
;
;
;
.
Кути зсуву фаз між фазною напругою і фазним струмом у фазах споживача та джерела відповідно дорівнюють один одному і можуть бути визначені так:
для споживача –
;
;
;
для джерела –
;
;
.
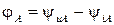Загальний вигляд суміщеної векторної діаграми струмів і фазних напруг при нерівнорозподіленому навантажені фаз зірки, за умовою Z N = 0, показаний на рис. 3.8.
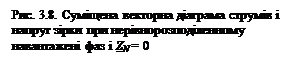
На відміну від попереднього випадку, тут 
. З аналізу діаграми випливає, що при зазначених умовах величина та напрямок вектору 
залежать від співвідношень між активними і реактивними опорами фаз споживача.
Аналіз з’єднання зіркою при Z a ¹ Z в ¹ Z c (Y а ¹ Y в ¹ Y c) і 0 < Z N <¥, як і у попередньому випадку, починають з розрахунку фазної напруги джерела і запису значень її комплексів:
;
;
;
.
Після цього визначають напругу зміщення нейтралі –
.
В силу того, що тут 
, фазні напруги споживача не будуть дорівнювати відповідним фазним напругам джерела.
Розрахувати комплекси фазних напруг споживача можна за другим законом Кірхгофа:
;
;
;
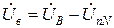Далі за законом Ома визначають комплекси фазних струмів споживача (вони ж лінійні струми):
;
;
;
і струм у нейтральному проводі –
.
Кути зсуву фаз між струмом і напругою у фазах споживача та джерела, а також кут зсуву фаз у нейтральному проводі визначають так:
у фазах споживача –
;
;
;
у фазах джерела –
;
;
;
у нейтральному проводі –
.
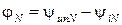Загальний вигляд векторної діаграми напруг при нерівнорозподіленому навантажені фаз зірки за умовою, що 0 < Z N < ¥, показаний на рис. 3.9. Як бачимо, для зазначених умов, внаслідок перекосу навантажень у фазах споживача (Z a ¹ Z в ¹ Z c) і тому, що , нейтральні точки джерела N і споживача n не співпадають за місцем розташування. З аналізу розрахунку та рис. 3.9 випливає, що більше навантажена фаза споживача знаходиться під меншою фазною напругою (Uа < UА), а менше завантажена – під більшою (Uв > UВ). При змінному у часі навантажені у фазах споживача за рахунок зміни величини і напрямку вектору 
нейтральна точка n споживача змінює своє місцеположення на векторній діаграмі. Отже, має місце “коливання” фазних напруг (Ua ¹ Uв ¹ Uc ¹ const) споживача, що надзвичайно негативно впливає на його роботу.
Векторна діаграма струмів при цьому принципово не відрізняється від векторної діаграми струмів попереднього варіанту – коли Z N = 0 (рис.3.8). Різниця полягає лише в тому, що вектори струмів джерела (лінійних струмів) і вектор струму нейтрального проводу показують такими, що виходять з нейтральної точки N джерела, а вектори струмів споживача (фазні, вони ж лінійні) – з нейтральної точки n споживача.
Порядок розрахунку і векторна діаграма з’єднання у зірку при відсутності нейтрального проводу (Z N = ¥), тобто трипровідної зірки, практично такі ж, як і у попередньому варіанті. Відміна полягає лише у тому, що внаслідок відсутності нейтрального проводу, маємо:
,
і, отже, додавання комплексів фазних або лінійних струмів –
,
тут роблять лише з метою перевірки правильності їх розрахунку.
Зазначимо, що при незмінному навантажені у фазах споживача, зі збільшенням опору нейтрального проводу величина “перекосу” напруг у фазах споживача зростає, а при обриві нейтрального проводу сягає максимуму. Для запобігання цьому у нейтральному проводі категорично забороняється встановлювати будь-які розмикаючі пристрої (вимикачі, запобіжники, тощо).
З’єднання у трикутник
При з’єднанні у трикутник (рис. 3.10) фази джерела або споживача послідовно з’єднають в єдиний замкнений контур.
Умовно прийнято, що для з’єднання у трикутник кінець X першої фази – фази А джерела, або фази а споживача з’єднують з початком (В, в) другої, кінець Y другої фази – з початком (С, с) третьої, кінець Z третьої – з початком першої. Для джерела з вузлів А, В, С виходять, а у споживача до вузлів а, в, с підводяться три лінійних проводи – проводи: A-a, B-в, C-c.
При роботі на холостому ході (без навантаження) потужного джерела трифазної напруги – трифазного генератора, що виробляє енергію з напругою до десятків кВ і фази якого мають опір десятки Ом та з’єднанні у трикутник, може скластися враження, що машина знаходиться у режимі короткого замикання. Між іншим, потрібно пам’ятати, що в симетричній трифазній системі фазні ЕРС зсунуті між собою на 120° (рис. 3.1). Тому для будь-якого моменту часу маємо:
.
До того ж, при відсутності навантаження струм у з’єднаних у трикутник обмотках трифазного генератора буде дорівнювати нулю.
Тут потрібно зауважити, що це вірно і ніякого короткого замикання немає, але тільки для трифазного генератора, який має три абсолютно однакові обмотки і при умові, що ці обмотки зсунуті між собою по колу статора чітко на 120° і що в них діють синусоїдні ЕРС. Оскільки ж на практиці виконати всі ці умови проблематично, то обмотки трифазних генераторів як правило з’єднують у зірку, а не у трикутник. З’єднання у трикутник застосовують тільки для споживачів.
Затискачі А, В, С обмоток трифазного генератора і трикутник споживача (рис. 3.11) з’єднують лінійними проводами А – а, В – в, С – с.
При з’єднанні у трикутник, як і при з’єднанні у зірку, розрізняють лінійні і фазні напруги, лінійні і фазні струми.
Нагадаємо, що лінійна U л– це напруга між початками двох будь-яких фаз джерела (
), або споживача (
). Фазна U ф – це напруга між початком і кінцем фази джерела (
) або споживача (). Прийнявши, що опори лінійних проводів дорівнюють нулю, неважко переконатися, що відповідні лінійні напруги джерела і фазні напруги споживача дорівнюють одна одній. Отже, при з’єднанні у трикутник маємо:
Струми (
), які діють у лінійних проводах (А – а, В – в, С – с) називають лінійними I л. Струми (), які діють у фазах джерела, або у фазах споживача (
) називають фазними I ф. Співвідношення між лінійними і фазними струмами визначимо за першим законом Кірхгофа. Рівняння для вузлів а, в, с будуть, відповідно:
;
;
.
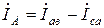З аналізу цих рівнянь випливає, що при будь-яких значеннях фазних струмів сума комплексів лінійних струмів трикутника дорівнює нулю –
.
Трикутник споживача (рис. 3.12, а) з рівнорозподіленим навантаженням у фазах – Z ав = Z вс = Z са = Z ф= r ф+ jx ф, підключений до джерела симетричної трифазної напруги U л, можна звести до вигляду, наприклад, як на рис. 3.12, б.
Отже, розрахунок такого з’єднання фактично зводиться до розрахунку однієї фази і може бути виконаний або класичним або символічним методами.
За класичним методом, фазні струми трикутника з рівнорозподіленим навантаженням згідно закону Ома будуть:
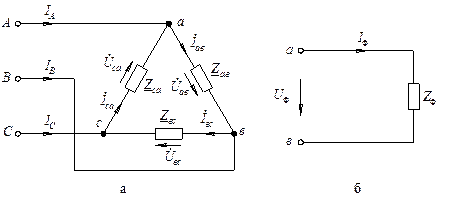
Для розрахунку фазних струмів трикутника символічним методом спочатку потрібно записати комплекси його фазних напруг. При цьому скористуємося умовами прийнятими ще при аналізі з’єднання у зірку (розділи 3.4.1 і 3.4.2) і на комплексній площині спрямуємо вектор фазної напруги 
джерела по вісі дійсних чисел. За такою умовою комплекси лінійних напруг джерела (вони ж - комплекси фазних напруг трикутника споживача), запишемо так:
;
;
.
Тоді фазні струми трикутника будуть:
;
;
;
Кути зсуву фаз у фазах з’єднання:
класичним методом –
;
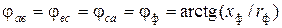символічним методом –
;
;
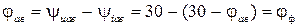Лінійні струми визначимо з використанням векторної діаграми (рис. 3.13), побудувавши за першим законом Кірхгофа трикутники струмів для вузлів а, в та с споживача.
Для цього, з кінця вектору 
, змінивши напрямок на протилежний, відкладемо вектор 
. З’єднавши початок вектора (початок координат), з кінцем вектору 
одержимо вектор 
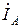. Для визначення 
та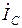 
аналогічним чином побудуємо трикутники струмів із сторонами 
та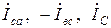 
.
З векторної діаграми видно, що “зірка” лінійних струмів 
з’єднання відстає від “зірки” фазних струмів 
споживача на кут 30°. Таким чином, кожен з побудованих трикутників струмів є рівнобедреним (бокові сторони – вектори фазних струмів, основа – вектор лінійного струму) з кутами при основі 30°. Неважко переконатися, що при цьому –
.
У загальному випадку комплекси лінійних струмів зазначеної схеми символічним методом розраховують за першим законом Кірхгофа:
;
;
.
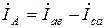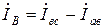Правильність їх визначення перевіряють на виконання умови –
.
При не рівнорозподіленому навантаженні у фазах трикутника споживача (Z ав ¹ Z вс ¹ Z са) кожну з фаз розраховують окремо символічним методом. У цьому випадку струми і кути зсуву фаз у фазах споживача, а також лінійні струми не будуть дорівнювати, відповідно, один одному. На векторній діаграмі при додаванні пар фазних струмів ми не отримуємо три рівнобедрених трикутники струмів. Отже, при не рівнорозподіленому навантажені фаз трикутника споживача маємо –
.
Підсумовуючи викладене у даному розділі, можна зробити такі висновки:
1. При з’єднанні у трикутник, так як і при з’єднанні у зірку, найбільш бажаним є рівнорозподілене навантаження фаз споживача. При цьому лінійні проводи з’єднання будуть в однаковій мірі навантажені струмом.
2. З’єднання фаз споживача у трикутник або у зірку дає можливість один і той же споживач приєднувати до трифазного джерела з різною лінійною напругою. Наприклад, у паспорті трифазного асинхронного двигуна вказують: 380/220® Y/D. Це означає, що при наявності джерела з U л = 380 В статорні обмотки двигуна потрібно з’єднувати у зірку, а при наявності джерела з U л= 220 В – у трикутник. При цьому в обох випадках фазна напруга статорних обмоток двигуна становитиме 220 В.
3. При однаковому навантажені фаз споживача, з’єднаного у трикутник, і споживача, з’єднаного у зірку, струм і, відповідно, а, отже, втрати, у лінійних проводах трикутника будуть більшими, ніж у лінійних проводах зірки. Тому на практиці, при наявності вибору між двома з’єднаннями, перевагу частіше віддають з’єднанню у зірку.
