Трифазні електричні кола
В сучасних умовах для промислових потреб виробляється, передається і розподіляється енергія багатофазної системи синусоїдних струмів.
Багатофазною електричною системою називають сукупність декількох електричних кіл, в яких діють періодичні ЕРС однієї частоти та однакової напруги, створені спільним джерелом електричної енергії і зсунуті між собою за фазою. Найбільше розповсюдження серед багатофазних електричних систем у промисловості отримала трифазна система, де джерелом електричної енергії є трифазний синхронний генератор. На практиці її використовують для живлення як трифазних, так і однофазних споживачів. Якщо ж повернутися до моделі пристрою отримання однофазного змінного струму, яку було розглянуто вище (рис. 2.3), то для отримання трифазного струму потрібно було б на одній осі пристрою розташувати три електрично незв’язані між собою рамки, площини яких зсунуті у просторі одна відносно одної за колом обертання.
Окремі електричні кола, які входять до складу такої системи називають фазами. На електричних схемах їх позначають великими буквами латинського алфавіту, наприклад для трифазної системи: А, В, С. На розподільчих пунктах шини трифазної системи виділяють відповідним кольором: фаза А – жовтим, В – зеленим, С – червоним.
Багатофазні (трифазні) електричні системи поділяють на симетричні і несиметричні; врівноважені і неврівноважені; зв’язані і незв’язані.
Симетричною багатофазною (трифазною) системою ЕРС (струмів) називають електричну систему, в якій генераторні ЕРС (струми) всіх фаз однакові між собою по величині і зсунуті за фазою одна відносно іншої на однаковий кут a.
,
де m – кількість фаз у багатофазній системі.
З рівняння випливає, що в трифазній симетричній системі, де m = 3, фазні ЕРС (рис. 3.1) зсунуті між собою на a = 2p/3 (тобто на 120°) і їх миттєві значення можна записати так:
;
;
.
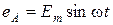При цьому комплекси діючих значень цих ЕРС будуть: 
;
;
.
Якщо система не відповідає вказаним вище умовам, то її називають несиметричною.
Врівноваженою трифазною називають систему, в якій діє симетрична система генераторних ЕРС та у якої комплекси опорів навантаження фаз однакові – Z а = Z в = Z с. За цих умов миттєва потужність такої системи не змінюється у часі і є величиною сталою. Це є визначальною перевагою трифазних систем у порівнянні з однофазними. Якщо система не відповідає вказаним умовам то її називають неврівноваженою.
Систему, у якій фази електрично не зв’язані між собою, називають незв’язаною. Якщо окремі фази джерела зв’язані між собою в електричному відношенні і з’єднані з зв’язаними фазами споживача, то таку систему називають зв’язаною.
Зазначимо, що у силовій електроенергетиці використовують тільки зв’язані системи, де фази джерела і фази споживача з’єднують у зірку Y або у трикутник D. При цьому, схема з’єднання фаз джерела (обмоток генератора) не залежить від схеми з’єднання опорів споживача і навпаки. Всього, комбінацій з’єднання фаз джерела і споживача може бути п’ять:D–D; D–Y; Y–D; Y–Y; Y–0–Y. Остання із схем з’єднання фаз джерела і споживача – зірка-зірка з нейтральним (нульовим) проводом, є чотирипровідною схемою, решта – трипровідні схеми.
З’єднання у зірку
На рис. 3.2, а наведена трифазна система, в якій три незв’язані між собою (в електричному відношенні) фази джерела електричної енергії (генератора) з’єднані шістьма проводами з трьома незв’язаними між собою споживачами.
Замінимо три зворотних проводи одним спільним (рис. 3.2, б), тобто з’єднаємо між собою три кінці (або три початки) фаз джерела і відповідно три кінці (або три початки) фаз споживача та отримаємо електрична зв’язану трифазну систему. З’єднання, в якому три кінці (або три початки) фаз джерела (або споживача) з’єднані у спільну точку, отримало назву з’єднання у зірку. Спільну точку, де з’єднані три кінці фаз джерела (або споживача) називають нейтральною або нульовою. Провід (N – n), який з’єднує нейтральну точку N джерела з нейтральною точкою n споживача називають нульовим проводом. Проводи (A – a, B – в, C – c), які з’єднують фази джерела з фазами споживача називають лінійними.
Струми, що діють у фазах джерела (
) або у фазах споживача (
), називають фазними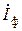 
. Струми (
), які діють у лінійних проводах, називають лінійними 
.
Легко впевнитись, що при з’єднанні у зірку відповідні лінійні і фазні струми дорівнюють один одному (
, 
, 
, 
), а струм 
, що діє у нейтральному проводі, може бути визначений на підставі першого закону Кірхгофа:
.
Напругу між початками двох будь-яких фаз джерела (
) або споживача (
) називають лінійною 
. Якщо вважати, що опори лінійних проводів дорівнюють нулю, то лінійні напруги джерела будуть дорівнювати відповідним лінійним напругам споживача (
, 
, 
) і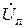 
при цьому може бути визначена як напруга між двома лінійними проводами.
Напругу між початком і кінцем фази джерела (
) або споживача (
) називають фазною 
. Але, для зручності, букви N і n в індексах фазних напруг джерела та споживача звичайно не вказують і записують ці напруги так: 
та 
. Якщо вважати, що опори лінійних і нульового проводів дорівнюють нулю, то може бути визначена як напруга між відповідним лінійним та нейтральним проводами.
Співвідношення між лінійними і фазними напругами можна визначити за другим законом Кірхгофа. Наприклад для джерела так:
; 
; 
.
Аналіз трифазних систем символічним методом звичайно починають з запису комплексів фазних і лінійних напруг джерела електричної енергії, прийняті значення яких залишають незмінними до повного завершення розрахунку. Так, сумістивши з дійсною віссю вектор будь-якої з фазних напруг джерела, наприклад 
, побудуємо векторну діаграму фазних напруг (зірку фазних напруг – рис. 3.3) джерела і запишемо значення їх комплексів:
; 
; 
.
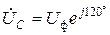Значення комплексів лінійних напруг джерела при цьому будуть:
;
;
.
Виконані алгебраїчні дії, стосовно визначення лінійних напруг джерела, покажемо на векторній діаграмі рис. 3.4. Так, для отримання 
з кінця вектору 
відкладемо вектор 
, змінивши його напрям на протилежний. З’єднавши початок з кінцем 
отримаємо:
.
Аналогічним чином отримуємо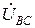 
і 
.
З записів значень комплексів фазних і лінійних напруг джерела та векторної діаграми видно, що зірка лінійних напруг джерела повернута відносно зірки його фазних напруг на кут 30° в додатному напрямку. Інколи лінійні напруги на векторній діаграмі розміщують у вигляді трикутника (на рис. 3.4 показані пунктиром), з центру тяжіння якого (нейтральної точки N) виходять вектори фазних напруг.
Оскільки у симетричного трифазного джерела всі фазні напруги за модулем дорівнюють одна одній і всі лінійні напруги також, то неважко переконатися, що для рівнобедреного трикутника зі сторонами, наприклад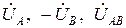 
, у якого кути при основані дорівнюють 30°, маємо:
.
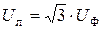Звідси випливає, що при лінійній напрузі джерела 660, 380 або 220 В його фазні напруги відповідно будуть: 380, 220 або 127 В.
Зірка споживача з рівнорозподіленим навантаженням фаз.
Рівнорозподіленим (симетричним) називають навантаження, при якому у кожну фазу ввімкнені споживачі, опори яких однакові між собою за величиною і характером. Тобто коли: Z a = Z в = Z c = Z ф.
Розглянемо випадок коли, до джерела симетричної трифазної напруги U л ввімкнені споживачі Z a = Z в = Z c = Z ф = r ф + jx ф, з’єднані у зірку (рис. 3.5, а).
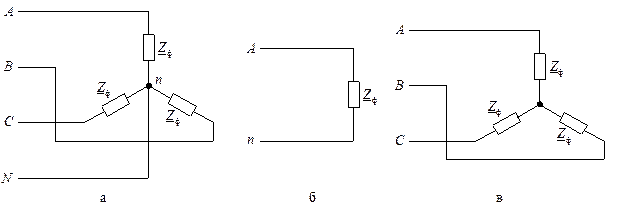
Нехтуючи опорами лінійних проводів, визначимо лінійні і фазні струми, кути зсуву фаз у фазах споживача та побудуємо суміщену векторну діаграму струмів і напруг з‘єднання.
Для трифазного джерела симетричної напруги U л маємо:
.
Оскільки опори лінійних проводів дорівнюють нулю, то внаслідок рівності лінійних напруг споживача та джерела маємо:
.
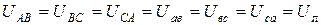Фазна напруга споживача також буде дорівнювати фазній напрузі джерела –
Враховуючи це, розрахунок трифазної системи при рівнорозподіленому навантажені фаз споживача може бути зведений до розрахунку тільки однієї фази, наприклад А (рис. 3.5, б). При цьому, розрахунок цієї фази може бути виконаний класичним або символічним методами.
Так, лінійні, вони ж фазні струми системи, за зазначених умов дорівнюють один одному і можуть бути визначені за законом Ома:
.
Кути зсуву фаз між фазною напругою і фазним струмом у фазах споживача також будуть дорівнювати один другому. Їх значення можна розрахувати так:
.
При виконанні розрахунку символічним методом, прийнявши, що:
;
;
;
за законом Ома розраховують комплекси лінійних (фазних) струмів:
;
;
.
Кути зсуву фаз у фазах джерела (вони же у фазах споживача) –
;
;
.
Неважко переконатися, що при рівнорозподіленому навантаженні у фазах споживача, струм у нейтральному проводі дорівнює нулю:
.
Отже, за таких умов схема з чотирипровідної (рис. 3.5, а) перетворюється у більш економічну трипровідну (рис. 3.5, в). Потрібно зазначити, що справедливим є і зворотне ствердження – якщо струм у нейтральному проводі дорівнює нулю, то зірка споживача має рівнорозподілене навантаження у фазах.
Загальний вигляд суміщеної векторної діаграми струмів і напруг при рівнорозподіленому навантажені фаз зірки показаний на рис. 3.6. На діаграмі пунктиром і без позначення показано, що в результаті додавання фазних (лінійних) струмів маємо 
.
