1.1. Количественный кинематический анализ.
Для проведения полного кинематического анализа заданной расчетной схемы (ЗРС) необходимо заменить опорные связи их шарнирно-стержневым аналогом и обозначить эти сечения (рис. 2.6).
Рис. 2.6
Степень статической неопределимости ЗРС определяется по формуле:
,
ü число жестких дисков системы: 
;
ü число простых шарниров, объединяющих жесткие диски системы: 
;
ü число опорных стержней: 
(
, 
).
Таким образом,
ЗРС статически определима.
1.2. Качественный кинематический анализ.
Проведем анализ на геометрическую неизменяемость ЗРС, которая обеспечивается наличием шарнирно-стержневого треугольника (ШСТ), образованного опорными связями, наложенными на диск (рис. 2.7).
Рис. 2.7
| ЗРС геометрически неизменяема |
Построение эпюр усилий
2.1. Построение грузовой эпюры изгибающих моментов от заданной нагрузки.
2.1.1. Определение опорных реакций.
Заменим опорные связи (рис. 2.6) на опорные реакции (рис. 2.8), причем одной реакции соответствует один опорный стержень. Реакции до их определения считаются положительно направленными.
| 
|
| Рис. 2.8 | Рис. 2.9 |
Найдем неизвестные реакции, используя уравнения равновесия (2.1):
 ;
 ;
 .
| (2.1) |
Заменяя введенные на рис. 2.8 обозначения реакций найденными векторами, получаем рис. 2.9 и используем его для проведения контроля правильности определения опорных реакций.
Контроль: 
.
При назначении контролируемых сечений на рис. 2.9 выделим один участок с законом изменения момента M=const (3–4), три участка с линейным законом изменения изгибающего момента (1–2, 5–6, 8–9) и один участок с параболическим законом (6–7–8).
2.1.2. Определение значений ординат и построение грузовойэпюры изгибающих моментов.
Найдем значения момента в контролируемых сечениях (рис. 2.10).
|  .
|
| 
 (РВ/Л),
(растянутые волокна поперечного сечения расположены слева от участка расчетной схемы).
|
| 
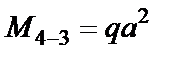 (РВ/Л).
|
| 
 (РВ/Л).
|
 Рис. 2.10
| 
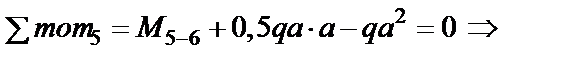
 (РВ/Н).
|
| 
 (РВ/Н).
|
| 
 (РВ/Н).
|
| 
 (РВ/Л);
 (РВ/Н).
|
Рис. 2.10 (окончание)
|  .
|
Рис. 2.11
2.2. Построение эпюры поперечных сил.
На рис. 2.11 рассмотрим участки, вдоль которых закон изменения изгибающего момента не меняет своего математического закона, и вычислим по ним ординаты поперечных сил как тангенс угла наклона касательной к эпюре изгибающих моментов (рис. 2.12).
|  .
|
|  .
|
|  .
|
|  ;
 .
|
Рис. 2.12
|  .
|
По результатам вычислений (рис. 2.12) построена эпюра поперечных сил, изображенная на рис. 2.13.
Рис. 2.13
2.3. Построение эпюры продольных сил.
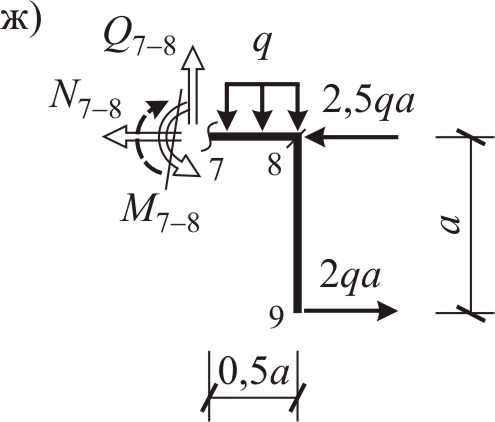
Вычисление ординат эпюры продольных сил N (рис. 2.14) на основе эпюры поперечных сил Q и узловой нагрузки методом последовательного вырезания узлов включает в себя:
1. Выбор последовательности вырезаемых узлов, содержащих не более двух неизвестных продольных усилий:
ü сначала рассматриваются узлы “1”, “4”, “9” и “8”, содержащие одно (рис. 2.14а, б, в) и два (рис. 2.14г) искомых продольных усилия;
ü затем рассматривается узел “2-3-5”, содержащий три неизвестных продольных усилия, в результате чего необходимо задаться численным значением одной из вертикальных продольных сил с учетом «инженерного» знака, используя найденное значение продольного усилия на этом участке бруса, т. е. 
(рис. 2.14д).
2. Формирование уравнений равновесия для каждого из узлов последовательности.
3. Вычисление ординат продольных усилий в узле из уравнений равновесия в проекциях на оси глобальной системы координат.
4. Присвоение «инженерного» знака полученным значениям: положительной принимается растягивающая (действующая «от узла») продольная сила.
| 
| 
|
 ;
 ;
 .
|  ;
 ;
 .
|  ;
 ;
 .
|
|   ;
  ;
 .
| |
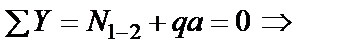
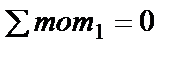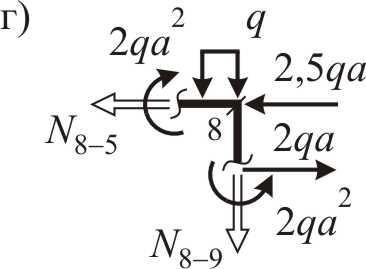
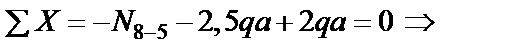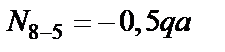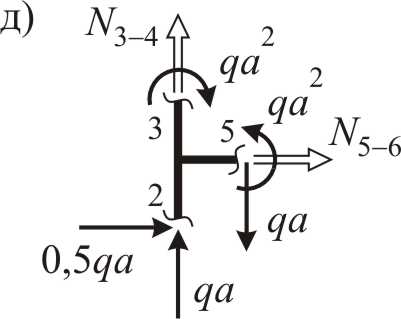Рис. 2.14
|   ;
  ;
 .
|
По результатам вычислений (рис. 2.14) построена эпюра продольных сил, изображенная на рис. 2.15.
Рис. 2.15
2.4. Контроль правильности определения ординат эпюр усилий.
Контроль правильности определения ординат эпюр усилий проводится для произвольной части ломаного бруса (рис. 2.16), для которой составляются уравнения равновесия (
, 
и 
).
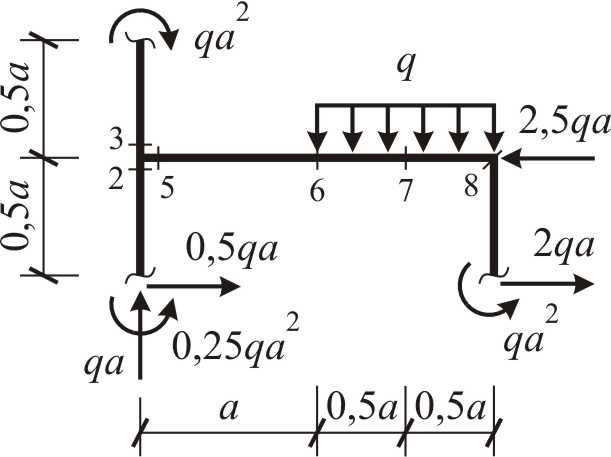Рис. 2.16
|  ;
 ;
|
Уравнения равновесия отрезанной части ЗРС удовлетворяются тождественно, что свидетельствует о значительной достоверности проведенных построений.
