МЕТОДИЧЕСКИЕ УКАЗАНИЯ
по выполнению
Расчетно-графической работы №1
Задача№2
Определение перемещений от статической нагрузки в ломаном брусе
по дисциплине «Строительная механика»
Тула 2012 г.
СОДЕРЖАНИЕ
Задание 2. Определение перемещений от статической нагрузки в
ломаном брусе................................................................................................ 2
Варианты заданий...................................................................................................................... 2
Пример выполнения задания................................................................................................... 7
1. Проведение кинематического анализа заданной расчетной схемы................... 7
1.1. Количественный кинематический анализ......................................................... 7
1.2. Качественный кинематический анализ............................................................. 8
2. Построение эпюр усилий................................................................................................. 8
2.1. Построение грузовой эпюры изгибающих моментов от заданной
нагрузки...................................................................................................................... 8
2.1.1. Определение опорных реакций............................................................... 8
2.1.2. Определение значений ординат и построение грузовойэпюры
изгибающих моментов............................................................................... 9
2.2. Построение эпюры поперечных сил................................................................ 11
2.3. Построение эпюры продольных сил................................................................ 12
2.4. Контроль правильности определения ординат эпюр усилий................... 13
3. Построение направляющих эпюр изгибающих моментов.................................. 14
3.1. Назначение вспомогательных расчетных схем............................................ 14
3.2. Построение направляющей эпюры изгибающих моментов от действия горизонтальной единичной сосредоточенной силы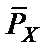 
в сечении K................................................................................................ 14
3.2.1. Определение опорных реакций............................................................. 14
3.2.2. Определение значений ординат и построение направляющей эпюры изгибающих моментов 
15
3.3. Построение направляющей эпюры изгибающих моментов от действия вертикальной единичной сосредоточенной силы 
в сечении K........................................................................................................ 16
3.3.1. Определение опорных реакций............................................................. 16
3.3.2. Определение значений ординат и построение направляющей эпюры изгибающих моментов 
17
3.4. Построение направляющей эпюры изгибающих моментов от
действия единичного изгибающего момента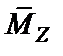 
в сечении K................. 19
3.4.1. Определение опорных реакций............................................................. 19
3.4.2. Определение значений ординат и построение направляющей эпюры изгибающих моментов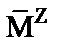 
19
4. Реализация матричной формы вычисления перемещений.................................. 21
4.1. Разработка схемы дискретизации..................................................................... 21
4.2. Матричная форма представления направляющих и грузовой эпюр...... 22
4.3. Построение матрицы податливости................................................................. 22
4.4. Приемы минимизации размеров матриц......................................................... 24
4.1.1. Способ вычеркивания в матрицах нулевых строк.......................... 24
4.1.2. Способ вычеркивания в матрицах одной из пары одинаковых строк 25
4.5. Вычисление искомых перемещений точки K................................................. 26
5. Построение схемы деформирования ЗРС................................................................. 27
Задание 2. Определение перемещений от статической нагрузки
в ломаном брусе
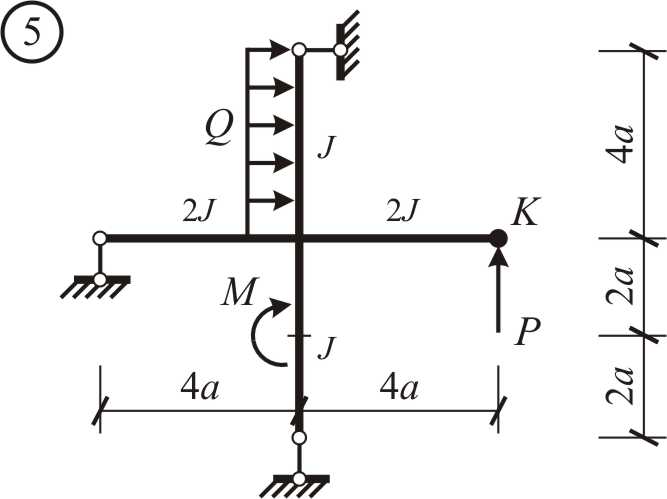
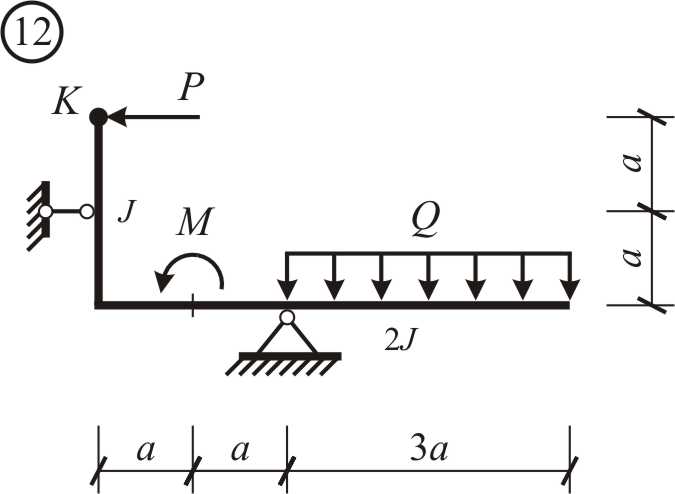
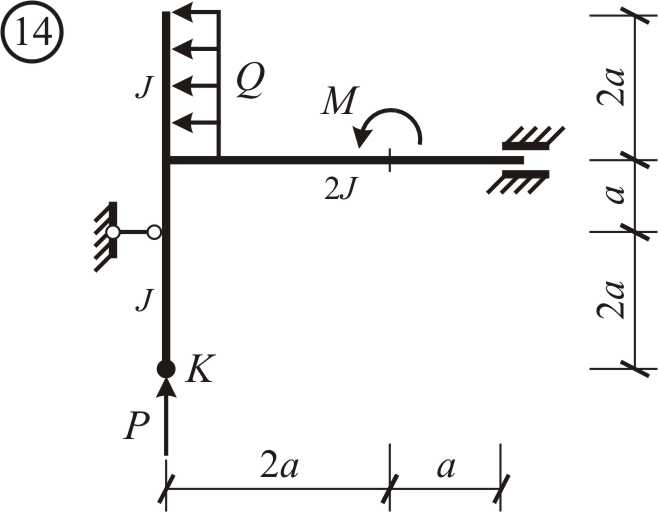
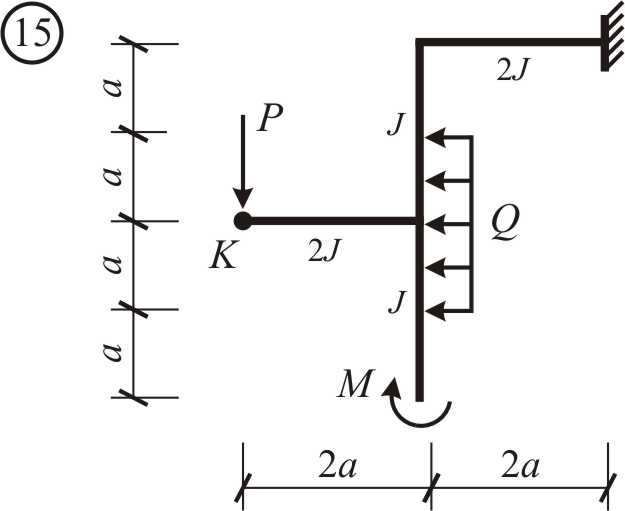
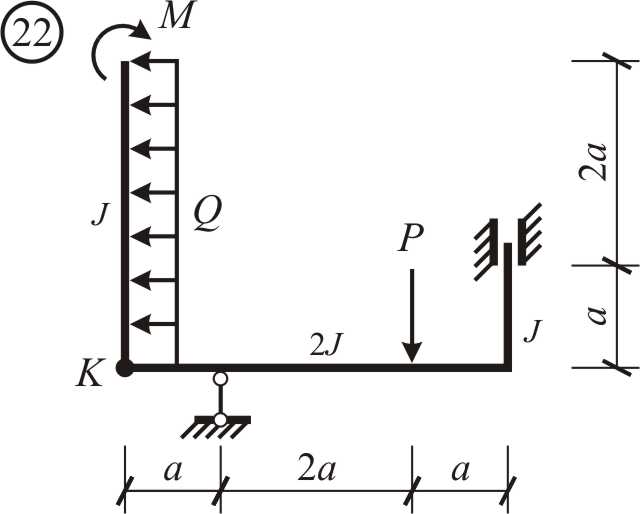
Варианты заданий. Для заданной расчетной схемы в виде ломаного бруса (рис. 2.1-2.4) необходимо:
1. Провести полный кинематический анализ.
2. Построить эпюры изгибающих моментов, поперечных и продольных сил.
3. Определить горизонтальное и вертикальное перемещения, а также угол поворота сечения K бруса в матричной форме.
4. Построить схему деформирования.
Необходимые для расчета данные указаны в табл. 2.1.
Таблица 2.1
| № варианта | P | М | Q | № варианта | P | М | Q |
| 1 | 2 qa | 3 qa 2 | q | 16 | 4 qa | 2 qa 2 | q |
| 2 | qa | 4 qa 2 | 3 q | 17 | 3 qa | 2 qa 2 | 2,5 q |
| 3 | 3 qa | qa 2 | 2 q | 18 | 3 qa | 4 qa 2 | q |
| 4 | 3 qa | 2 qa 2 | 3 q | 19 | 2 qa | qa 2 | 3 q |
| 5 | qa | 4 qa 2 | 3 q | 20 | qa | 2 qa 2 | 3 q |
| 6 | 2 qa | qa 2 | 0,5 q | 21 | 2 qa | 4 qa 2 | q |
| 7 | 3 qa | 2 qa 2 | q | 22 | 4 qa | 2 qa 2 | 2 q |
| 8 | 3 qa | qa 2 | 2 q | 23 | 3 qa | 2 qa 2 | q |
| 9 | 2 qa | 4 qa 2 | 3 q | 24 | 3 qa | 3 qa 2 | q |
| 10 | 2 qa | qa 2 | 1,5 q | 25 | qa | 3 qa 2 | 3 q |
| 11 | 2 qa | 3 qa 2 | q | 26 | 4 qa | 2 qa 2 | 3 q |
| 12 | 2 qa | 4 qa 2 | 3 q | 27 | 3 qa | 4 qa 2 | q |
| 13 | 4 qa | 2 qa 2 | q | 28 | qa | 5 qa 2 | q |
| 14 | 2 qa | 3 qa 2 | q | 29 | 4 qa | 4 qa 2 | 1,5 q |
| 15 | qa | 4 qa 2 | 3 q | 30 | 5 qa | 3 qa 2 | 3 q |
| 
|
| 
|
| 
|
| 
|
Рис. 2.1
| 
|
| 
|
| 
|
| 
|
Рис. 2.2
| 
|
| 
|
| 
|
| 
|
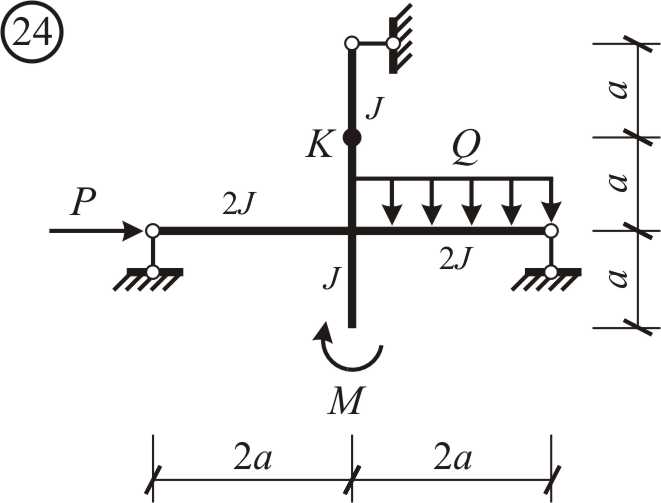
Рис. 2.3
| 
|
| 
|
| 
|
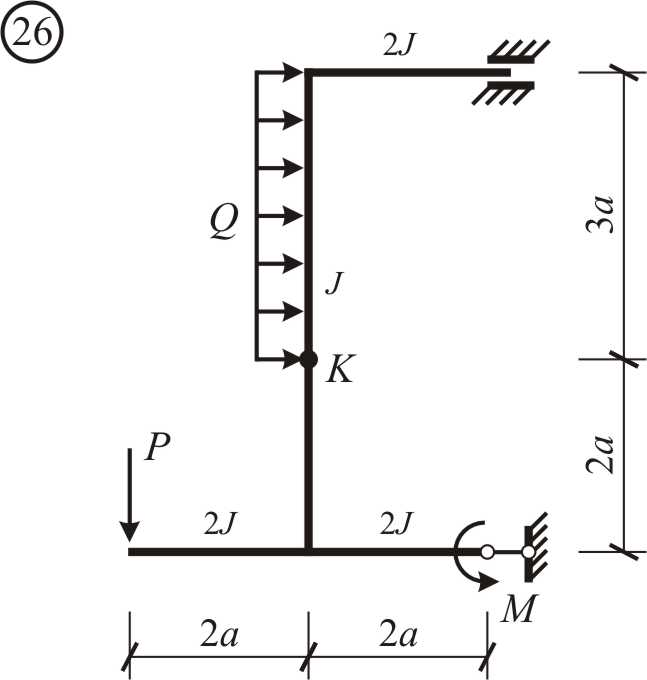
Рис. 2.4
Пример выполнения задания.
Дано: расчетная схема (рис. 2.5) с указанием моментов инерции ее сечений, кратных масштабу J.
Требуется построить эпюры усилий в ломаном брусе, а также схему деформирования заданной расчетной схемы, определив все перемещения сечения K в матричной форме.
| Рис. 2.5 |
Решение
Особенностью ломаного бруса в сравнении с однопролетной балкой является наличие в его сечениях продольных усилий, возникающих даже от поперечной нагрузки.
