Каждый эксперимент содержит элемент неопределенности вследствие ограниченности информации. Постановка параллельных опытов не дает полностью совпадающих результатов, потому что всегда существует ошибка опыта. Для ее определения опыт воспроизводится по возможности в одинаковых условиях несколько раз и затем берется среднее арифметическое всех результатов
где n – число параллельных опытов.
где 
– результат параметра оптимизации l – го повторения i – го опыта;
– среднее арифметическое значение всех n повторений i – го опыта.
Таким образом, ставится серия одинаковых опытов n, затем проверяется однородность дисперсий, т.е. выясняется, определяются ли различные значения у с одинаковой точностью по критерию Кохрена
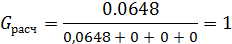
Расчетное значение G – критерия сравнивают с табличным в зависимости от уровня значимости 
, числа степеней свободы f = п — 1 и числа опытов N. Ряд дисперсий считается однородным, если G расч < G табл. 1< 0,9065, то есть ряд дисперсий неоднородный.
Проверка адекватности модели
Она необходима для того, чтобы ответить на вопрос — можно ли использовать полученное уравнение или необходима более сложная модель.
Адекватность модели проверяют с помощью критерии Фишера
где 
– дисперсия неадекватности,
Здесь yiрасч , yiэксп — значения параметра оптимизации в i- м опыте, соответственно рассчитанные по уравнению регрессии и определенные экспериментально; k — число коэффициентов уравнения регрессии, включая b0. 
Гипотеза об адекватности уравнения принимается в том случае, когда рассчитанное значение F -критерия не превышает табличного для выбранного уровня значимости и числа степеней свободы f1, и f2, с которым определялись дисперсии неадекватности опыта.
6,62 < 7,7, то есть наша модель адекватна.
Проверка статической значимости коэффициентов модели
Прежде всего, рассчитывается дисперсия в определении коэффициентов
Коэффициент считается значимым, когда его абсолютная величина больше доверительного интервала, т. е.
где t — критерий Стьюдента (берется из таблиц в зависимости oт уровня значимости а и числа степеней свободы при определении дисперсии опыта, табл. П2);
Sbj — среднеквадратичная ошибка определения коэффициентов
регрессии 
.
То есть значимые коэффициенты являются коэффициенты уравнения по максимальным окружным деформациям.
Приложение
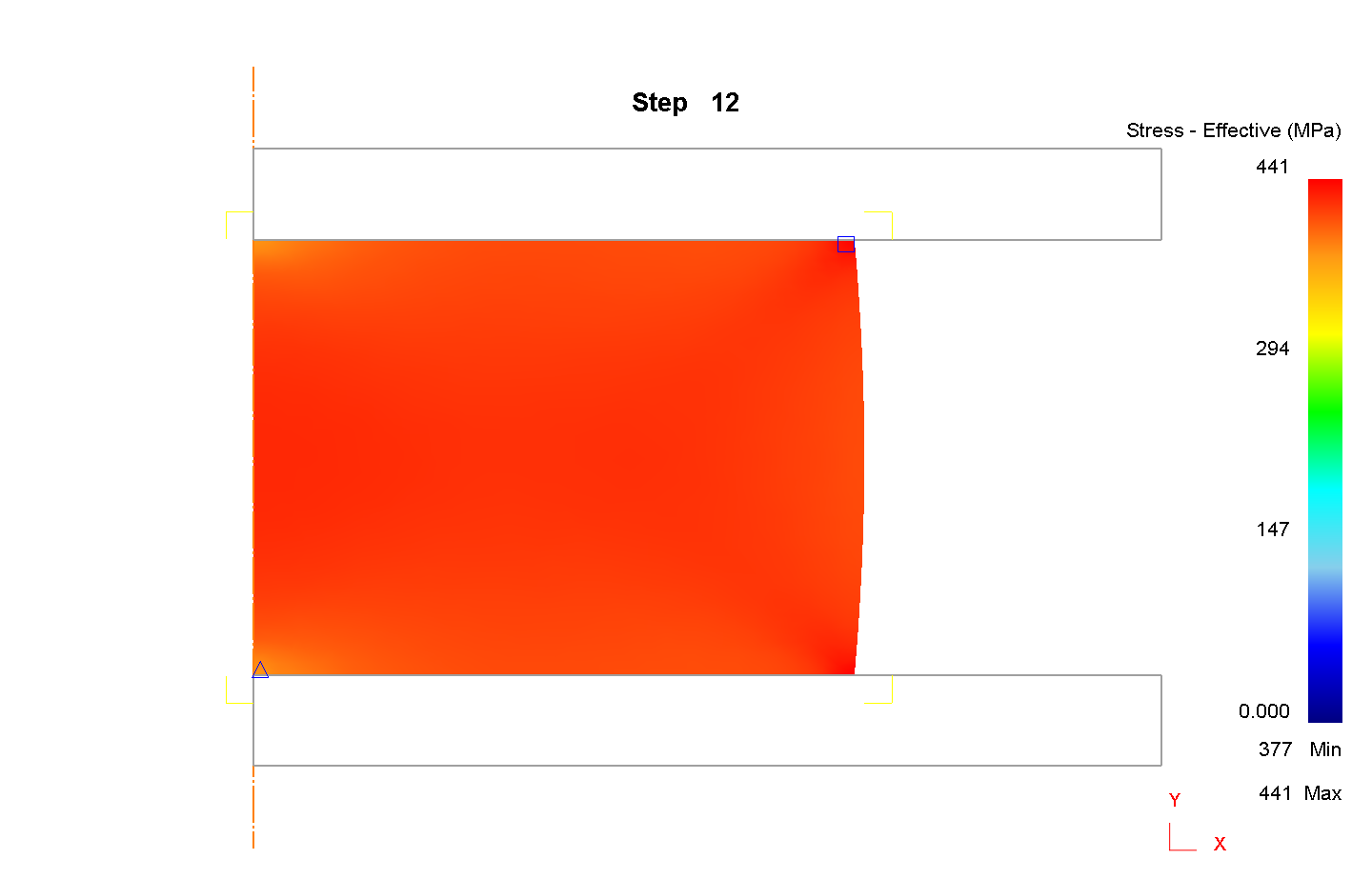
I. Для ε=40%, μ=0,3
1) Сетка 1000 элементов
2) Сетка 900 элементов
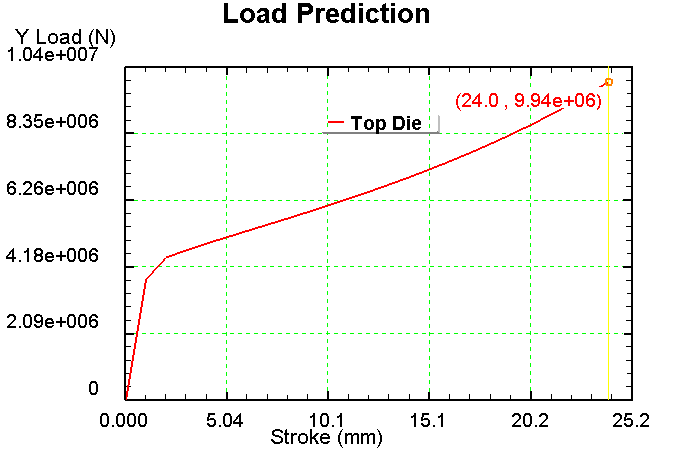
II. Для ε=20%, μ=0,3
1) Сетка 1000 элементов
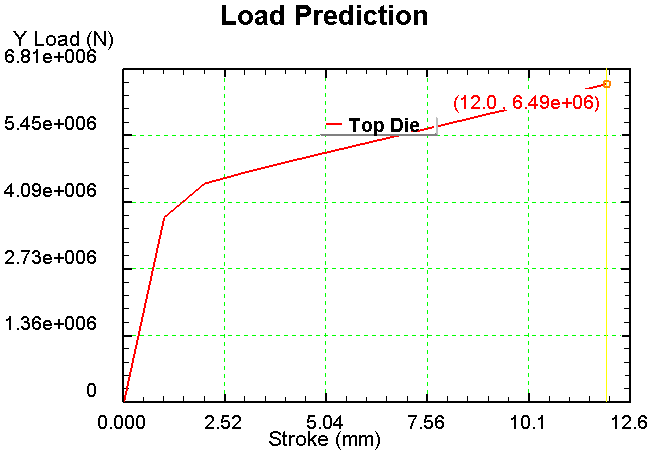
2) Сетка 900 элементов
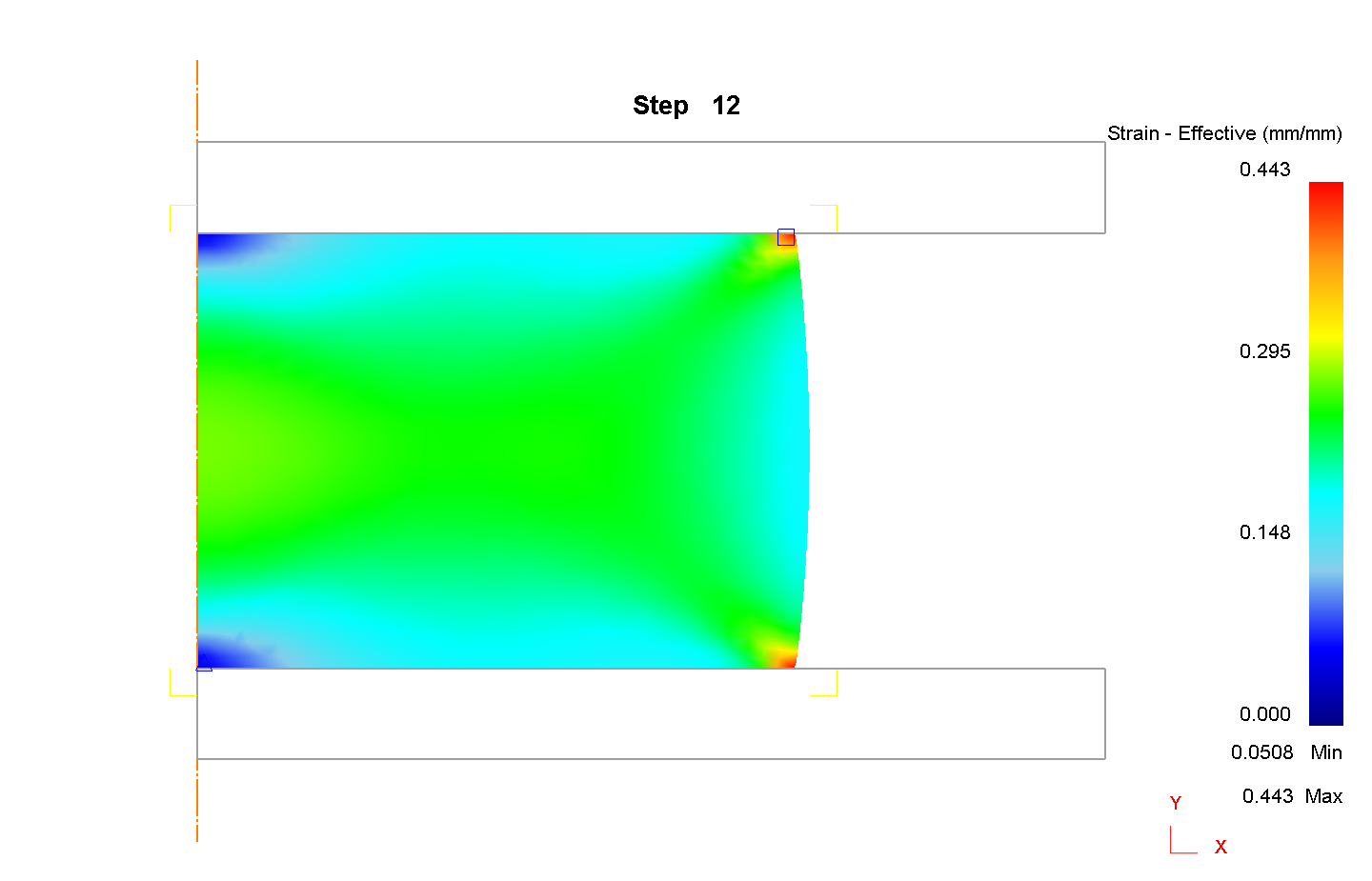
III. Для ε=40%, μ=0,2
1) Сетка 1000 элементов
2) Сетка 900 элементов 
IV. Для ε=40%, μ=0,2
1) Сетка 1000 элементов 
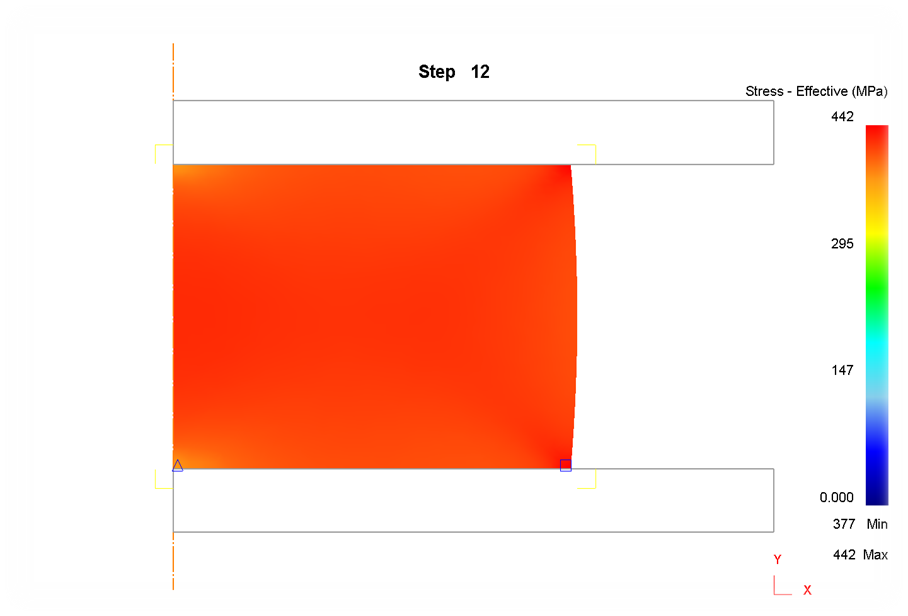
2) Сетка 900 элементов
