При анализе и представлении результатов исследований необходимо по возможности стремиться к использованию простых функций. Для этого применяют метод выравнивания, заключающийся в том, что кривую,
построенную по экспериментальным точкам, представляют линейной функцией.
Для преобразования некоторой кривой в прямую линию вводят новые переменные:
X=fl(x,y),Y=f2(x,y) (3)
В искомом уравнении они должны быть связаны линейной зависимостью
У=а + bХ (4)
Значения X и Y можно вычислить на основе решения системы уравнений (3). Далее можно построить прямую, по которой легко графически
вычислить параметры а (ордината точки пересечения прямой с осью Y) и b (тангенс угла наклона прямой с осью X): b=tgb=(Yi-a)/Xi
При графическом определении параметров а и bобязательно, чтобы прямая (4) строилась на координатной сетке, у которой началом является точка Y=0 и Х=0. Для расчета необходимо точки Yi и Xi принимать на крайних участках прямой.
Для определения параметров прямой можно применить также другой графический метод. В уравнение (4) подставляют координаты двух крайних точек, взятых с графика. Получают систему двух уравнений, из которых вычисляют а и b. После установления параметров а и bполучают эмпирическую формулу (4), которая связывает Y и X, позволяет установить функциональную связь между х и у и эмпирическую зависимость (1).
Пример: подобрать эмпирическую формулу, описывающую результаты следующих измерений:
| X | |||||||
| Y | 12,1 | 19,2 | 25,9 | 33,3 | 40,5 | 46,4 | 54,0 |
Графический анализ этих измерений показывает, что в прямоугольных координатах точки хорошо ложатся на прямую линию, следовательно, нет необходимости выравнивания, и их можно выразить зависимостью (2). Выбираем координаты крайних точек и подставляем в (2). Тогда, а +7b= 54,0; а +1b= 12,1, откуда при совместном решении данных выражений следует b= 41,9/6=6,98 и а=12,1—6,98=5,12. Эмпирическая формула примет вид у= 5,12+6,98х.
Таким образом, аппроксимация экспериментальных данных прямолинейными функциями позволяет просто и быстро установить вид эмпирических формул.
Однако данный метод имеет существенные погрешности, т.к. координаты крайних точек заранее признаются лежащими на прямой.
Линеаризацию кривых можно легко осуществить на полу- или логарифмических координатных сетках, которые сравнительно широко применяют при графическом методе подбора эмпирических формул.
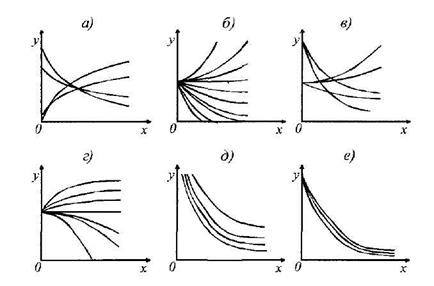
Выравнивание может быть применено в тех случаях, когда экспериментальная кривая на сетке прямоугольных координат имеет вид плавной кривой. Так, если экспериментальный график имеет вид, показанный на рисунке 1а, то необходимо применить формулу
y = ахb (5)
Заменяя X=lgx и Y=lgy, получим Y=lga+bX. При этом экспериментальная кривая превращается в прямую линию на логарифмической сетке.
Если экспериментальный график имеет вид, показанный на рисунке 1 б, то целесообразно использовать выражение
y = ахb (6)
При замене Y=Igy получим Y=lga+bxlge. Здесь экспериментальная кривая превращается в прямую линию на полулогарифмической сетке.
Если экспериментальный график имеет вид, представленный на рисунке 1в, то эмпирическая формула принимает вид
у = с + axb (7)
Если bзадано, то надо принять Х=х, и тогда получим прямую линию на сетке прямоугольных координат у=с+аХ. Если же bнеизвестно, то надо принять X=lgx и Y=lg(y — с), в этом случае будет прямая линия, но на логарифмической сетке Y=lga+bX.
В последнем случае необходимо предварительно вычислить с. Для этого по экспериментальной кривой принимают три произвольные точки х1, y1; х2, y2 и x3= √x1·x2; y3 и вычисляют с в виде отношения
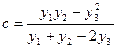 (8)
(8)
Если экспериментальный график имеет вид, показанный на рисунке 1, то можно пользоваться формулой
y=c+ + ахbx ( 9 )
|
Рисунок 1 - Примерный вид графиков эмпирических формул
Путем замены Y=lg(y — с) можно построить прямую на полулогарифмической сетке:
Y=lga + bxlge, (10)
где с предварительно определяется, используя формулу (8).
В этом случае х3 = 0,5(х1+х2).
Если экспериментальный график имеет вид, представленный на рисунке 1д, то применяется выражение
y=a+b/x (11)
Путем замены x=l/z можно получить прямую линию на прямоугольной сетке координат y=a+bz.
Если график имеет вид, соответствующий кривым на рисунке 1е, то используется формула
у=1/(а+bх) (12)
Если принять y=l/z, то z=a+bx, т.е. прямая на прямоугольной сетке координат.
Аналогично, уравнению
y=1/(a+bx+ cx 2) ( 13 )
путем замены y=l/z можно придать вид z=a+bx+ cx 2.
Пример: пусть, необходимо подобрать эмпирическую формулу для следующих результатов:
| X | 1,5 | 2,0 | 2,5 | 3,0 | 3,5 | 4,0 | 4,5 | |
| У | 15,2 | 20,6 | 27,4 | 36,7 | 49,2 | 66,0 | 87,4 | 117,5 |
На основе данных строится график (рисунок 2а), вид графика в прямоугольных координатах соответствует кривым, представленным на
рисунке 16 у - ае bx.

Рисунок 2 - Экспериментальный график в прямоугольных и полулогарифмических координатах.
После логарифмирования выражения lgy=lga-bxlge.
Если обозначить lgy=Y, то Y= Iga+bxlge, т.е. в полулогарифмических координатах выражение для Y представляет собой прямую линию (рисунок 2б). Подстановка в уравнение координат крайних точек дает IgI 5,2=lga+blge и lgII7,5=lga+4,5blge.
Следовательно,
lga+ blge=1,183
Iga+4,5 blge=2,070
откуда b=0,887/(3,5lge) =0,579; lga=l,183-0,254=0,929\ 'a=l,85.
Окончательно эмпирическая формула будет иметь вид у=I,85*е0,579x.
При подборе эмпирических формул широко используются степенные полиномы
у=ао+а1х+а 2 х2+а3 х3... аm хm (14)
Такой вид формулы удобен для анализа, его члены легко дифференцируются и интегрируются, полиномами можно аппроксимировать любые результаты, если они графически выражаются непрерывными функциями.
Задача сводится к нахождению неизвестных коэффициентов степенного полинома (а0, а1, а2.....а m), при этом количество неизвестных коэффициентов должно быть меньше чем количество экспериментальных точек.




