(метод фрактального сжатия графической информации)
Два названия метода в заголовке взаимно дополняют друг друга. Первое отражает, скорее, алгоритм декодирования (воспроизведения по коду) «сжатого» изображения (IFS – Iterated Function System, – система (комплекс) итерированной функции); второе указывает класс объектов (изображений), изучение которых привело к разработке данного способа кодирования.
1. Понятие фрактала. Канторово множество
Упрощённо говоря, фрактал – геометрическая фигура (множество точек), каждая часть которой подобна всей фигуре. Сразу представить примеры такой конструкции непросто, поскольку в описании подразумевается бесконечная повторяемость в структуре, что в классических построениях геометрии не встречается. Природными объектами, имеющими сходную структуру, являются, например, ветви дерева, облака, береговая линия.
Исторически одним из первых хорошо изученных фракталов была конструкция, представленная общественности немецким математиком Георгом Кантором в конце XIX века, – канторово множество. Рассмотрим подробнее его построение.
В качестве стартовой конфигурации берётся отрезок [0;1]. Он делится на 3 равные по длине части, из которых удаляется средняя, более точно, интервал (1/3; 2/3). Оставшиеся отрезки снова делятся на 3 равные по длине части, из которых удаляются средние интервалы (1/9; 2/9) и (7/9; 8/9).
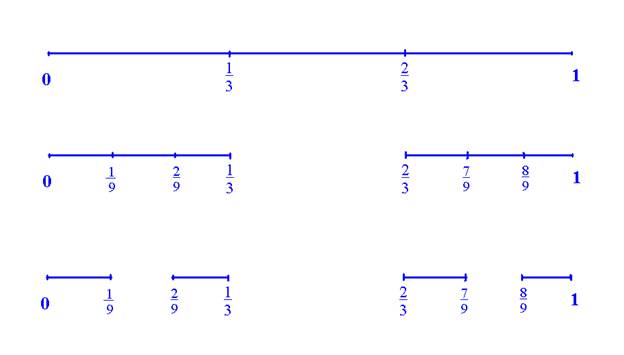
Рис.
И так далее, на новом шаге каждый из оставшихся отрезков делится на 3 равные по длине части, из которых удаляется находящаяся посередине (интервал). Интерес представляет множество, получающееся в пределе данных итераций (канторово). Обозначим его C.
Канторово множество обладает многими примечательными свойствами, отметим наиболее важные в контексте нашей тематики.
i) C – фрактал.
Действительно, в ходе построения к каждому меньшему отрезку применяются те же преобразования, что и ко всему [0;1].
ii) Мера («сколько места занимает» на прямой) множества C равна нулю.
Действительно, C содержится в наборе отрезков, образующихся на любом шаге построения. Суммы длин отрезков в таких наборах составляют последовательность 1, 2/3, 4/9, …, 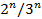 , … из чего и следует утверждение. Этот же факт можно проиллюстрировать, если вычислить сумму длин всех удаляемых в процессе построения C интервалов:
, … из чего и следует утверждение. Этот же факт можно проиллюстрировать, если вычислить сумму длин всех удаляемых в процессе построения C интервалов:
 +
+  +
+ 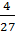 + … +
+ … + 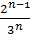 + … = /
+ … = / 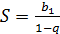 / =
/ = 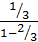 = 1.
= 1.
iii) Мощность множества C равна мощности [0;1].
Действительно, можно установить взаимно однозначное соответствие (отображение) между элементами (числами) этих множеств. Для задания такого отображения Кантор предложил записать числа множества C в троичной системе, а числа всего [0;1] – в двоичной.
Поскольку в таких записях можно использовать (см. ниже) только отрицательные степени тройки и двойки соответственно, то нахождение записей имеет простой геометрический смысл, связанный с делением [0;1] на равные по длине части. Проиллюстрируем идею только для троичной системы. Пусть x – некоторое число из [0;1). Значение первой цифры после запятой в его троичной записи – 0, 1 или 2, – геометрически определяется тем, в какую треть [0;1) попадает точка, соответствующая числу x. Если в [0;1/3), то 0; если в [1/3;2/3), то 1; если в [2/3;1), то 2. Значение следующей цифры получается аналогично после деления на три равные части той трети [0;1), в которой оказалась точка x. И т. д.
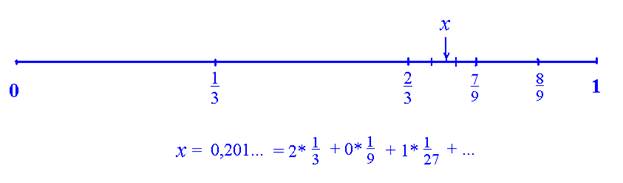
Рис.
Таким образом, точки (числа) канторова множества, кроме правых границ отрезков деления, имеют в своей троичной записи только цифры 0 или 2. При этом хорошо известно, что как раз границы деления дробных разрядов (правые границы соответствующих отрезков) в любой системе представления (по любому основанию) имеют две записи. Например, число 1 = 1,0 в десятичной системе может быть записано и как 0,(9). Действительно,
0,99…9… = 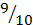 +
+ 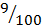 + … +
+ … + 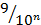 + … =
+ … = 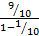 = 1.
= 1.
Точно так же в троичной системе имеем:
1 = 1,0 = 0,(2); 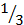 = 0,1 = 0,0(2);
= 0,1 = 0,0(2); 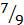 = 0,21 = 0,20(2) и т.д.
= 0,21 = 0,20(2) и т.д.
Получается, что все точки (числа) множества C, и только они, могут иметь дробную запись в троичной системе, состоящую из цифр 0 и 2. Каждое число [0;1] имеет дробную запись в двоичной системе, состоящую из цифр 0 и 1 (число 1 представляем в виде 0,(1)). Взаимно однозначное соответствие между множествами [0;1] и C определяется схемой:
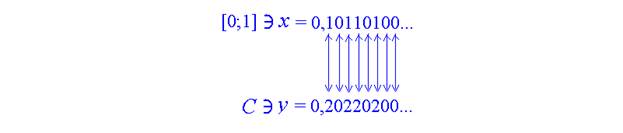
Рис.
Как известно, единичный отрезок имеет мощность континуума (мощность множества действительных чисел).
Аналитическое задание канторова множества
Важным шагом в изучении фракталов была разработка способов их компьютерного построения. Этапы построения канторова множества можно описать при помощи преобразований, задаваемых формулами.
Первый этап – переход от [0;1] к набору из двух отрезков [0;1/3] 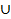 [2/3;1] (от множества
[2/3;1] (от множества 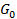 к множеству
к множеству 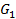 ), – можно осуществить путём объединения результатов действия двух преобразований сжатия. A и B. Где A – сжатие с k=1/2 относительно точки 0, B – сжатие с k=1/2 относительно точки 1. Т.е.
), – можно осуществить путём объединения результатов действия двух преобразований сжатия. A и B. Где A – сжатие с k=1/2 относительно точки 0, B – сжатие с k=1/2 относительно точки 1. Т.е. 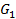 = A(
= A(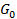 )
) 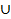 B(
B(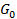 ).
).
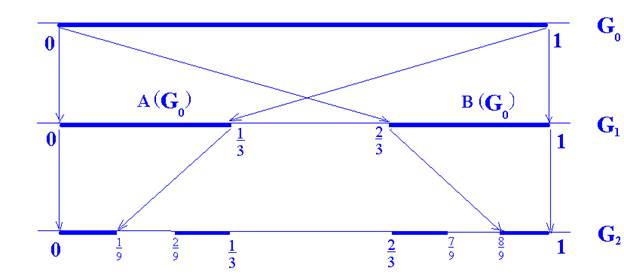
Рис.
Легко увидеть, что 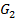 = A(
= A(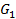 )
) 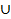 B(
B(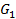 ),
), 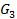 = A(
= A(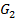 )
) 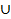 B(
B(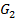 ) и т.д.
) и т.д.






