В общем случае для объяснения корреляционной матрицы потребуется не один, а несколько факторов. Каждый фактор характеризуется столбцом, каждая переменная - строкойматрицы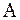 
. Фактор называется генеральным, если все его нагрузки значительно отличаются от нуля и он имеет нагрузки от всех переменных. Генеральный фактор имеет нагрузки от всех переменных и схематически такой фактор изображен на рис.1. столбцом 
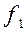.Фактор называется общим, если хотя бы две его нагрузки значительно отличаются от нуля. Столбцы 
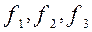, на рис. 1. представляют такие общие факторы. Они имеют нагрузки от более чем двух переменных. Если у фактора только одна нагрузка, значительно отличающаяся от нуля, то он называется характерным фактором (см. столбцы 
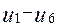на рис. 1.) Каждый такой фактор представляет только одну переменную. Решающее значение в факторном анализе имеют общие факторы. Если общие факторы установлены, то характерные факторы получаются автоматически. Число высоких нагрузок переменной на общие факторы называется сложностью. Например, переменная 
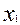на рис.1. имеет сложность 2, а переменная 
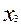- три.
Рис. 1. Схематическое изображение факторного отображения. Крестик означает высокую факторную нагрузку.
Итак, построим модель
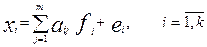, (4)
где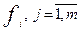 
- ненаблюдаемые факторы m < k,
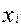- наблюдаемые переменные (исходные признаки),
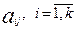- факторные нагрузки,
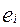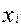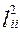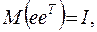
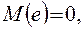
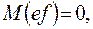
- случайная ошибка связанная только с с нулевым средним и дисперсие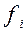й 
:
и 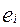- некорpелированы,
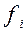- некоррелированные случайные величины с нулевым средним и единичной дисперсией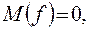 
.
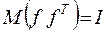Тогда
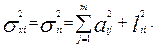(5)
Здесь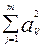 
- i -ая общность представляющая собой часть дисперсии 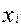, обусловленная факторами, 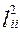- часть дисперсии 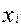, обусловленная ошибкой. В матричной записи факторная модель примет вид:
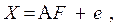(6)
где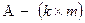 
- матрица нагрузок, 
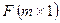- вектор факторов, 
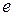- вектор ошибок.
Корреляции между переменными, выраженные факторами, можно вывести следующим образом:
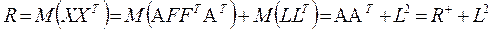, (7)
где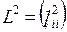 
- диагональная матрица порядка 
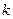, содержащая дисперсии ошибок[i]. Основное условие: 
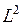- диагональная, 
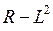- неотрицательно определенная матрица. Дополнительным условием единственности решения является диагональность матрицы 
.
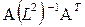Имеется множество методов решения факторного уравнения. Наиболее ранним методом факторного анализа является метод главных факторов, в котором методика анализа главных компонент используется применительно к редуцированной корреляционной матрице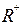 
с общностями на главной диагонали. Для оценки общностей обычно пользуются коэффициентом множественной корреляции между соответствующей переменной и совокупностью остальных переменных.
Факторный анализ проводится исходя из характеристического уравнения, как и в анализе главных компонент:
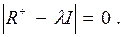(8)
Решая которое, получают собственные числа λi и матрицу нормированных (характеристических) векторов V, и затем находят матрицу факторного отображения:
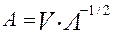
Для получения оценок общностей и факторных нагрузок используется эмпирический итеративный алгоритм, который сходится к истинным оценкам параметров. Сущность алгоритма сводится к следующему: первоначальные оценки факторных нагрузок определяются с помощью метода главных факторов. На основании корреляционной матрицы R формально определяются оценки главных компонент и общих факторов:
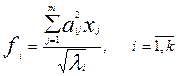(9)
где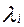 
- соответствующее собственное значение матрицы R;
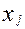- исходные данные (вектор-столбцы);
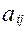- коэффициенты при общих факторах;
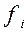- главные компоненты (вектор-столбцы).
Оценками факторных нагрузок служат величины
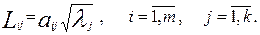(10)
Оценки общностей получаются как
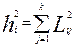(11)
На следующей итерации модифицируется матрица R - вместо элементов главной диагонали подставляются оценки общностей, полученные на предыдущей итерации; на основании модифицированной матрицы R с помощью вычислительной схемы компонентного анализа повторяется расчет главных компонент (которые не являются таковыми с точки зрения компонентного анализа), ищутся оценки главных факторов, факторных нагрузок, общностей, специфичностей. Факторный анализ можно считать законченным, когда на двух соседних итерациях оценки общностей меняются слабо.
Примечание. Преобразования матрицы R могут нарушать положительную определенность матрицы R+ и, как следствие, некоторые собственные значения R+ могут быть отрицательными.
Для лучшей интерпретации полученных общих факторов к ним применяется процедура вращения. Если факторный анализ ведется в терминах главных компонент, то значения факторов могут быть вычислены непосредственно. В случае вращения главных компонент соотношения, связывающие исходные переменные и значения факторов, несколько усложняются. Ниже в матричном виде приведено соотношение, оптимальное по скорости вычисления, а также независимое от метода вращения факторов:
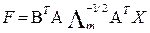(12)
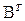- повернутая матрица A,
A - матрица коэффициентов при общих факторах,
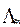- диагональная матрица m собственных членов,
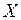- матрица исходных данных,
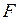- матрица m повернутых факторов.
При определении числа общих факторов руководствуются следующими критериями: число существенных факторов можно оценить из содержательных соображений, в качестве числа общих факторов m берется число собственных значений, больших либо равных единице (по умолчанию), выбирается число факторов, объясняющих определенную часть общей дисперсии или суммарной мощности
Литература по теме 6:
1. Окунь Я. Факторный анализ/ пер. с польск. – Москва: «Статистика», 1974. - 200 с.
- Дубров А.М., Мхитарян В.С., Трошин Л.И. Многомерные статистические методы/ - Москва, «Финансы и статистика», 2000. - 352
[i] Дубров А.М., Мхитарян В.С., Трошин Л.И. Многомерные статистические методы/ - Москва, «Финансы и статистика», 2000. - 352 с.
