Способы задания функции двух переменных

ОСНОВНЫЕ ПОНЯТИЯ ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ (ФНП)

ПЛАН

1. Определение функции нескольких переменных (ФНП).

2. Способы задания функции двух переменных.

3. Предел и непрерывность ФНП.

4. Частные и полное приращения функции двух переменных.

5. Частные производные первого порядка функции двух

переменных и их геометрическая интерпретация

Определение ФНП.

При изучении многих явлений приходится встречаться с функциями двух и более независимых переменных. Приведем примеры.

Пример 1. Площадь S прямоугольника со сторонами, длины которых равны х и у вычисляется по формуле: S = х · у, где S – является функцией двух переменных т.к. каждой паре значений х и у соответствует определенное значение площади S.

Пример 2. Объем V прямоугольного параллелепипеда с ребрами, длины которых равны х, у, z определяется по формуле V = x y z.

Здесь V – функция трех переменных x, y, z.

Определение. Функцией n переменных х₁, х₂,…,х_n,

где (х₁, х₂,…,х_n) ÎDÌ Rⁿ будем называть правило или

закон, по которому каждому набору переменных

(х₁, х₂,…,х_n) ÎD ставится в соответстие единственное число

у ÎЕ Ì R. Тот факт, что задана функция n переменных

будем записывать следующим образом: у = f (х₁, х₂,…,х_n).

Мы будем рассматривать функции двух переменных, т.к. основные факты теории функций нескольких переменных наблюдаются уже на функции двух переменных, а также для функций двух переменных можно дать геометрическую интерпретацию.

Определение.Функцией двух переменных х, у будем называть правило

или закон, по которому каждой паре чисел (х, у) Î D

ставится в соответствие единственное число z Î Е.

Тот факт, что задана функция двух переменных, будем записывать в виде: z = f(x, у). При этом х и у будем называть независимыми переменными (аргументами), а z – зависимой переменной (функцией).

Множество D(z) называется областью определения функции. Множество Е значений, принимаемых z в области определения, называется областью изменения функции.

Функцию двух переменных z = f(х, у ), где (х, у) Î D можно рассматривать как функцию точки М(х, у) координатной плоскости Оху.

Значение функции z = f(х, у ) в точке М₀ (х₀, у₀) называют частным значением функции и обозначают одним из способов:

z(х₀, у₀), , f(х₀, у₀).

Способы задания функции двух переменных

Функция двух переменных, как и функция одной переменной, может быть задана разными способами.

1) Аналитический способ состоит в том, что функция z представлена с помощью формулы. Если при этом область определения D(z) не указана, то под ней понимают множество таких пар значений (х, у), при которых заданная формула имеет смысл. Областью определения может быть вся плоскость или её часть, ограниченная некоторыми линиями. Линию, ограничивающую область, называют границей области. Точки области, не лежащие

на границе, называются внутренними. Об-

ласть, состоящая только из внутренних точек,

называется открытой, область с присоеди-

ненной к ней границей называется замкнутой

областью. Например, функция

z = ln (4 – х ² – у ²) имеет областью определе-

Рис. 1 ния внутреннюю часть круга х ² + у ² < 4

(открытая область, рис. 1).

2) Табличный способ. В первой строке таблицы выписываются возможные значения переменной х: х ₁, х ₂, …, х _n, в первом столбце – значения переменной у: у ₁, у ₂, …, у _n, на пересечении строки и столбца указывается соответствующее значение функции, например:

z ₁₁ = z(x ₁, y ₁ ), z _ij = z(x_i, y_j) (i = 1, 2, …, n; j = 1, 2, …, n).

у / х	х₁	х₂	×××	x_i	×××	x_n
y₁	z₁₁	z₂₁	×××	z_m₁	×××	z_n₁
y₂	z₁₂	z₂₂	×××	z_m₂	×××	z_n₂
…	…	…	×××	…	×××	×××
у_i	z_1j	z_2j	×××	z_ij	×××	z_nj
×××	×××	×××	×××	×××	×××	×××
y_n	z₁_n	z_2n	×××	z_i_n	×××	z_n_n

3) Графический способ. Примем z за аппликату некоторой точки

P(х, у, z) в пространстве. Всей области D(z) соответствует множество точек Р, образующее в пространстве некоторую поверхность. Графиком функции z = f(х, у) в прямоугольной декартовой системе координат в пространстве является поверхность, каждая точка которой - Р(х, у, f(х, у)).

Если поверхность является графиком функции двух переменных, то уравнение, определяющее эту функцию, является уравнением поверхности.

Например, функция имеет областью определения круг х² + у² £ 9 (рис.2) и изображается верхней полусферой с центром в точке О(0, 0, 0) и радиусом R = 3 (рис. 3).

Рис. 2 Рис. 3

Предел функции

Понятия предела функции двух (и более) переменных и непрерывности вводится аналогично понятию предела и непрерывности функции одной переменной.

Определение. Расстоянием от точки М₁ (х₁, у₁) до точки М₂ (х₂, у₂) назо-

вем число: .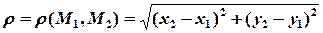

Определение.d-окрестностью точки М₀ (х₀, у₀) назовем множество всех

точек М (х, у) плоскости, таких, что r(М, М₀) < d.

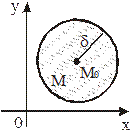Геометрически d-окрестность точки М₀ – это все внутренние точки круга с центром М₀ и радиусом d (рис. 4).

Пусть функция z = f(х, у) определена в не-

которой окрестности точки М₀ (х₀, у₀), кроме быть

может, самой этой точки.

Рис. 4

Определение. Число b называется пределом функции z = f(х, у) в точке

М₀ (х₀, у₀), если для любого сколь угодно малого положи-

тельного числа 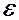> 0 существует d > 0 такое, что для всех

точек М(х, у) Î D(z), отличных от точки М₀ и удовлетво-

ряющих неравенству r(М, М₀) < d выполняется неравен-

ство │ f(х, у) – b │ < .

Записывается так или .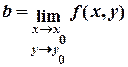

Из определения следует, что если предел существует, то он не зависит от пути, по которому точка М стремится к точке М₀.