Для облегчения ряда теплотехнических расчётов Д.У. Гиббсом была предложена функция I, называемая в настоящее время энтальпией термодинамической системы (вещества, тела) (устаревшие названия – теплосодержание и тепловая функция Гиббса), определяемая как
I = U + PV. (5.4.1)
Энтальпия I, как и внутренняя энергия U, является экстенсивным параметром, так как её величина пропорциональна массе ТС и обладает свойством аддитивности. Интенсивными параметрами являются удельная i = I / M и молярная im = I / nm = im энтальпии, которые соответственно определяются как:
i =и + Pv, im =иm + PVm, (5.4.2)
где [ i ] = Дж/кг; [ im ] = Дж/моль.
Удельная и молярная энтальпии, как и и, и иm, свойствами аддитивности не обладают. В технических расчётах в термодинамике в основном используется i, поэтому в дальнейшем в основном будем рассматривать только её, тем более, что переход от i к I или im никаких трудностей не представляет.
Так как и является функцией состояния ТС, а P и v основными термодинамическими параметрами её состояния, то i также является функцией состояния Т. Поэтому она может быть определена через три или два основных термодинамических параметра i = f (P, v, T) или i = f 1 (P, v), i = f 2 (P, Т), i = f 3 (Т, v) и, как и и, обладает полным дифференциалом, например:
. (5.4.4)
Поэтому изменение i полностью определяется начальным и конечным состояниями ТС и не зависит от вида ТП, то есть D i = i 2 - i 1, где i 1, i 2 – удельные энтальпии соответственно в начальном и конечном состояниях ТС, Дж/кг. Соответственно в циклах 
.
Следует напомнить, что в циклах изменение функций ТП, то есть D q и D lд, не обращаются в нуль, как это имеет место с изменениями функций состояния, D и и D i, а определяются площадью ограниченной кривой процесса, например площадью S1-3-2-4-1 на рассмотренной ранее рабочей диаграмме.
Продифференцировав первое уравнение (5.4.2), получим:
или 
. (5.4.6)
Подставив последнее выражение в (5.3.3), получим:
. (5.4.7)
Данное уравнение является вторым видом уравнения 1-го закона термодинамики для закрытых ТС. Проинтегрировав (5.4.7), получаем:
или
. (5.4.8)
Из (5.4.8) следует, что изменение i в рассматриваемом ТП будет отличаться от поступающего в ТС (покидающего ТС) тепла q на величину располагаемой работы lрас.
Для изобарного ТП из (5.4.7) и (5.4.8) следует, что:
dq = di и q = Di (Т 1 … Т 2) = i 2 – i 1, (5.4.9)
то есть тепло в этом ТП расходуется только на изменение энтальпии, причём это справедливо не только для идеального газа, а и для реальных веществ. Таким образом, энтальпию веществ можно определить как физическую величину, изменение которой в любых ТП, равно количеству тепла, поглощённого или отданного этим веществом в изобарном ТП, протекающем в тех же температурных границах, что и рассматриваемый ТП.
В адиабатном ТП, когда dq = 0 и q = 0, имеем:
dlpас = - di и lp ас= -(i 2 – i 1) = i 1 – i 2, ( 5.4.10)
Если подставить правую часть (5.2.2.15) в правую часть (5.3.3), то получим 1-й закон термодинамики для потока (открытых ТС)наличие в котором слагаемого dlтр делает его справедливым как для равновесных, так и неравновесных ТП:
. (5.4.11)
Но 
, поэтому (5.4.11) может быть записано в виде:
. (5.4.12)
Уравнение 1-го закона термодинамики в таком виде широко применяется для исследования газовых потоков, так как в него входит их важнейшая характеристика - скорость движения w.
Учитывая уравнение Клапейрона, можно 1-е уравнение (5.4.2) представить в виде:
. (5.4.13)
Ранее неоднократно отмечалось, что и идеального газа зависит только от его Т. Только от Т зависит и произведение RT. Поэтому величина i идеального газа также будет зависеть только от его Т, и следовательно, (5.4.9) для идеального газа будет справедливо для любых ТП, в которых имеет место изменение Т.
Энтальпией ТС удобно пользоваться в тех случаях, когда в качестве независимых переменных, определяющих состояние ТС, выбирают Р и Т.
Выполненными исследованиями установлено, что изменение i в изобарном процессе определяется как:
. (5.4.18)
Выражение (5.4.18) будет справедливо для любых веществ при любом ТП, хотя и получено для частного случая - изобарного ТП.
Интегрируя (5.4.18) в диапазоне температур от Т = Т1 = 0 К до
Т = Т 2, получим абсолютную величину i (Т 2) при данном Р:
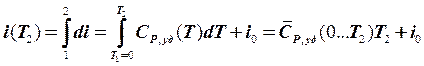, (5.4.19)
где i 0 – постоянная интегрирования, физический смысл которой – i вещества при Т = 0 К и данном Р, Дж/кг; 
- температурная зависимость истинной изобарной удельной теплоёмкости, определённая соответственно при данном Р, Дж/(кг × К).
В теплотехнических расчётах обычно определяют не абсолютную величину i, а D i в ходе ТП, протекающих при соответствующем Р:
(5.4.20)
Изменения молярной Dim (Т 1… Т 2) и объёмной Diоб (Т 1… Т 2) энтальпий определяются аналогично Di (Т 1… Т 2). В этом случае в формуле (5.4.20) вместо 
необходимо использовать соответственно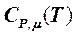 
и 
.
У ряда газов наиболее широко применяющихся в теплотехнике и рассматриваемых как идеальные газы, условно принято считать i = 0 при
t = 0 0C. Для этих газов (5.4.20) в температурной шкале Цельсия принимает вид:
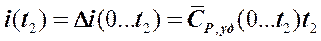. (5.4.21)
Из всех газовых смесей наиболее широкое применение в горном деле нашли влажный воздух, продукты сгорания различных видов органического топлива и водяной пар. Для практических расчётов их термодинамических величин в технической литературе предложено несколько довольно простых эмпирических выражений. С ними необходимо ознакомиться самостоятельно в Части 3, подраздел 5.4.
Для газов, которые в соответствующих ТП можно рассматривать как идеальные, а также для жидкостей и твёрдых веществ при отсутствии в последних фазовых переходов в (5.4.19)…(5.4.21) могут использоваться 
, полученные при Р» 0,1 МПа и приводимые обычно в справочной литературе.
Для ряда веществ при стандартных условиях их состояния в химической термодинамике в настоящее время экспериментально определены величины i. Такая i получила название стандартной удельной энтальпии и обозначение i 0 (298). При известной i 0 (298) абсолютная величина i вещества при Т 2 > 298,15 К, то есть i 0 (Т 2), может быть вычислена аналогично и 0 (Т 2):
где 
- температурная зависимость истинной изобарной удельной теплоёмкости, определённая при Р = Р 0 = 1 атм, Дж/(кг × К).
При наличии фазовых переходов D i веществ определяется уже с учётом тепла фазовых переходов. Так i вещества в диапазоне температур от Т 1 до Т 2, где Т 1 < Тпл, а Т 2 > Тисп; Тпл, Тисп – температуры соответственно плавления и испарения вещества, К, при данном Р определяется как
где iпл, iисп – удельная скрытая теплота соответственно плавления и испарения вещества (в современной технической литературе их стали называть удельными энтальпиями плавления и испарения веществ), Дж/кг. Индексы в (5.4.41) «тв», «ж» и «п» означают твёрдую, жидкую и паровую фазы вещества.
Зная удельную энтальпию фазового перехода вещества iф.п . при
Р = const, можно найти изменение его удельной внутренней энергии при этом переходе, Duф.п. :
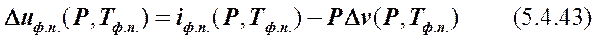
где Тф.п. – температура фазового перехода, К; Dv (P,T 2) – изменение удельного объёма вещества в процессе фазового перехода, м3/кг.
С рядом известных формулировок 1-го закона термодинамики и их анализом вам необходимо познакомиться самостоятельно в Части 3, подраздел 5.5.
