Вычисление определенного интеграла по формуле
Ньютона-Лейбница
Вычисление определенного интеграла, как предела интегральных сумм, сложно даже для простейших функций. Необходим простой способ вычисления определенных интегралов, минуя отыскание интегральных сумм и переход к пределу. Этот метод, основанный на связи определенного интеграла с вычислением первообразной, выражается формулой Ньютона-Лейбница.
Теорема. Пусть функция 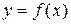 непрерывна на отрезке
непрерывна на отрезке  и F(x) –
и F(x) –
любая первообразная для f(x) на  . Тогда определенный инте-
. Тогда определенный инте-
грал от функции f(x) на  равен приращению первообразной
равен приращению первообразной
F(x) на этом отрезке:
 . (25)
. (25)
Доказательство. Разобьем отрезок  точками
точками  ,
, 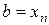
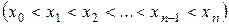 на n -частичных отрезков
на n -частичных отрезков  , …,
, …, 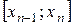 (рисунок 10).
(рисунок 10).
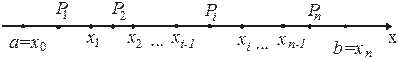
Рисунок 10
Рассмотрим тождество 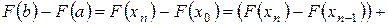
 .
.
Преобразуем каждую разность в скобках по теореме Лагранжа
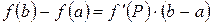 . (26)
. (26)
Получаем 
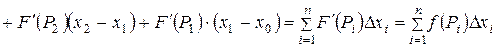 ;
;
следовательно, 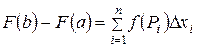 , (27)
, (27)
где  есть некоторая точка интервала
есть некоторая точка интервала  .
.
Так как функция 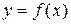 непрерывна на
непрерывна на  , то она интегрируема на
, то она интегрируема на  . Поэтому существует предел интегральной суммы, равный определенному интегралу от
. Поэтому существует предел интегральной суммы, равный определенному интегралу от 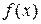 на
на  .
.
Переходя в равенстве (27) к пределу при 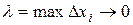 , получаем
, получаем
 , т.е.
, т.е. 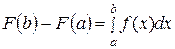 .
.
Равенство (25) называется формулой Ньютона-Лейбница.
Если ввести обозначения  , то формулу Ньютона-Лейбница (25) можно переписать в виде:
, то формулу Ньютона-Лейбница (25) можно переписать в виде: 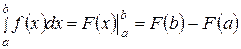 .
.
Читается формула (25) так: чтобы вычислить определенный интеграл от непрерывной функции f(x) на отрезке  , надо найти ее первообразную функцию
, надо найти ее первообразную функцию  и взять разность значений этой первообразной на концах отрезка
и взять разность значений этой первообразной на концах отрезка  :
:  .
.
Замечание 1. Мы ввели понятие  для случая
для случая  . Его можно обобщить и на случай
. Его можно обобщить и на случай  . Сделаем это так, чтобы формула Ньютона-Лейбница оставалась справедливой.
. Сделаем это так, чтобы формула Ньютона-Лейбница оставалась справедливой.
Положим, по определению, что для 
 . (28)
. (28)
Проверим справедливость формулы Ньютона-Лейбница:
 .
.
Принимая во внимание (28), для нас отныне будет несущественно, какой из пределов интегрирования больше: верхний или нижний.
Эта формула имеет место и для  :
:  .
.
Замечание 2. Величина интеграла 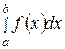 не зависит от того, какой буквой обозначена переменная интегрирования, т.е.
не зависит от того, какой буквой обозначена переменная интегрирования, т.е. 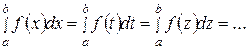 , а зависит лишь от вида подынтегральной функции и отрезка интегрирования, поскольку смена обозначений такого рода никак не влияет на поведение интегральной суммы.
, а зависит лишь от вида подынтегральной функции и отрезка интегрирования, поскольку смена обозначений такого рода никак не влияет на поведение интегральной суммы.
Формула Ньютона-Лейбница дает практически удобный метод вычисления определенных интегралов в том случае, когда известна первообразная подынтегральной функции.
Только с открытием этой формулы определенный интеграл смог получить то значение в математике, какое он имеет в настоящее время. Эта формула значительно расширила область применения определенного интеграла, так как математика получила общий метод для решения различных задач частного вида и поэтому смогла значительно расширить круг приложений определенного интеграла.
Пример 10. Вычислить определенные интегралы: а)  ; б)
; б) 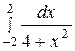 ;
;
в)  .
.
Решение. а) 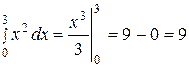 .
.
б)  .
.
в) 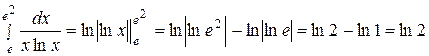 .
.
Пример 11. Найти массу прямолинейного стержня  , плотность которого в каждой точке
, плотность которого в каждой точке  равна
равна 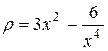 .
.
Решение. По формуле (21) имеем: 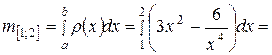
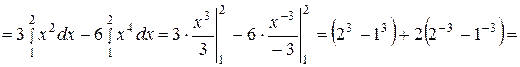
 (ед.массы).
(ед.массы).
Дальнейшие свойства определенного интеграла
2.1. Теорема о среднем. Если функция 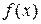 непрерывна на отрезке
непрерывна на отрезке  , то существует точка
, то существует точка 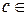
 такая, что
такая, что
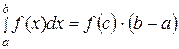 . (29)
. (29)
Доказательство. По формуле Ньютона-Лейбница имеем  , где
, где  .
.
Применяя к разности  теорему Лагранжа, получим
теорему Лагранжа, получим 
 .
.
Теорема о среднем при  имеет простой геометрический смысл: значение определенного интеграла равно, при некотором
имеет простой геометрический смысл: значение определенного интеграла равно, при некотором 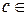
 , площади прямоугольника с высотой
, площади прямоугольника с высотой 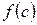 и основанием
и основанием  (рисунок 11). Число
(рисунок 11). Число
 (30)
(30)
называется средним значением функции 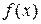 на отрезке
на отрезке  .
.
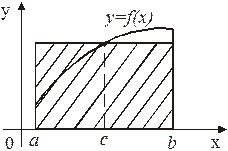
Рисунок 11
2 .2 Свойство неотрицательности.
Если функция 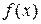 сохраняет знак на отрезке
сохраняет знак на отрезке  , где
, где  , то интеграл
, то интеграл 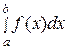 имеет тот же знак, что и функция:
имеет тот же знак, что и функция:
если 
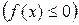 на отрезке
на отрезке  , то
, то

 . (31)
. (31)
Доказательство. По теореме о среднем 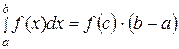 , где
, где  .
.
Так как  для всех
для всех 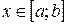 , то и
, то и  , а
, а  , поэтому
, поэтому  , т.е.
, т.е.  , что требовалось доказать.
, что требовалось доказать.
2.3. Неравенство между непрерывными функциями на отрезке  ,
, 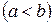 можно почленно интегрировать.
можно почленно интегрировать.
Если  при
при 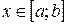 , то
, то
 . (32)
. (32)
Доказательство. Так как  , то при
, то при  согласно свойству 6 имеем
согласно свойству 6 имеем 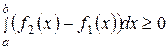 , а по свойству 2
, а по свойству 2 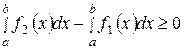 , т.е.
, т.е.
 .
.
Оценка интеграла.
Если m и М – соответственно наименьшее и наибольшее значения функции 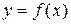 на отрезке
на отрезке  , (
, ( ), то
), то
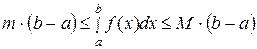 . (33)
. (33)
Доказательство. Так как для любого 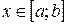 имеем
имеем 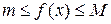 , то, согласно свойству 7, имеем
, то, согласно свойству 7, имеем  .
.
Применяя к крайним интегралам свойства 1 и 4, получаем
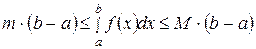 .
.
Если  , то свойство 8 иллюстрируется геометрически: площадь криволинейной трапеции заключена между площадями прямоугольников, основание которых есть отрезок
, то свойство 8 иллюстрируется геометрически: площадь криволинейной трапеции заключена между площадями прямоугольников, основание которых есть отрезок  , а высоты равен m и М соответственно (рисунок 12).
, а высоты равен m и М соответственно (рисунок 12).

Рисунок 12
2.5. Модуль определенного интеграла не превосходит интеграла от модуля подынтегральной функции:
 . (34)
. (34)
Доказательство. Применяя свойство 7 к очевидным неравенствам 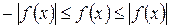 , получаем
, получаем  .
.
Отсюда, по определению модуля, следует, что 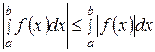 .
.
2.6. Производная определенного интеграла по переменному верхнему пределу равна подынтегральной функции, в которой переменная интегрирования заменена этим пределом, т.е.:
 . (35)
. (35)
Доказательство. По формуле Ньютона-Лейбница имеем: 
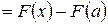 . Следовательно,
. Следовательно,  .
.
Это обозначает, что определенный интеграл с переменным верхним пределом есть одна из первообразных подынтегральной функции.
Методы интегрирования
Для нахождения определенного интеграла применяют методы интегрирования, аналогичные методам интегрирования в неопределенном интеграле. Рассмотрим основные из них.






