ПЛАН
1. Непосредственное интегрирование, метод разложения
подынтегральной функции.
2. Метод интегрирование по частям.
3. Метод замены переменной.
Непосредственное интегрирование, метод разложения
Подынтегральной функции.
Непосредственным интегрированием называют метод нахождения неопределенных интегралов с помощью таблицы интегралов и свойств неопределенного интеграла.
Методом разложения подынтегральной функции называют такое нахождение неопределенных интегралов, когда подынтегральную функцию преобразуют к такому виду, при котором затем возможно будет применение непосредственного интегрирования.
Пример 1. Вычислить интеграл
Решение. Запишем функцию в виде
.
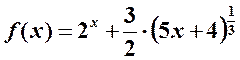Так как интеграл суммы равен сумме интегралов, то
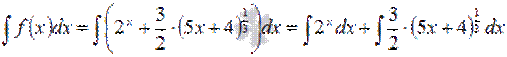
Числовой коэффициент можно вынести за знак интеграла:
Первый из интегралов приведен к табличному виду, поэтому из таблицы первообразных для показательной функции имеем
Для нахождения второго интеграла 
воспользуемся таблицей первообразных для степенной функции
и правилом 
Получим
Следовательно,
где 
Пример 2. Вычислить следующие интегралы: а) 
; б) 
; в) 
; г) 
; д) 
.
Решение. а) 
.
б)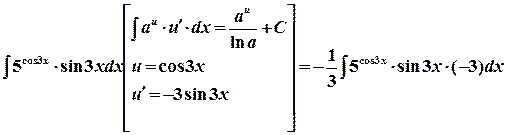 
=
.
в) 
=
= 
.
г) 
= 
.
д) 
.
Метод интегрирования по частям
Среди правил дифференцирования есть правила вычисления производных произведения и частного. Для интегрирования таких общих правил нет, поэтому операция нахождения первообразной - более сложная, зачастую использующая искусственные, не всегда очевидные преобразования.
Большое значение имеет метод интегрирования по частям.
Теорема. Пусть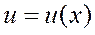 
и 
- некоторые дифференцируемые функции.
Тогда 
(2)
Доказательство. По свойству дифференциала 
или 
. Интегрируя левую и правую части последнего равенства, получаем 
; 
, что и требовалось доказать.
Формулу (2) называют формулой интегрирования по частям для неопределенного интеграла. При ее применении фиксируется разбиение подынтегрального выражения искомого интеграла на два сомножителя (
и 
). При переходе к правой части первый из них u дифференцируется (его называют дифференцируемым множителем), второй 
интегрируется (его называют интегрируемым множителем), причем 
.
Возможности применения формулы (2) связаны с тем, что дифференцирование может существенно упростить один из сомножителей в подынтегральном выражении (при условии, что интегрирование не слишком усложняет другой).
Иногда эту формулу приходится использовать несколько раз.
Укажем некоторые типы интегралов, которые удобно вычислять методом интегрирования по частям.
1. Интегралы вида 
, где 
- многочлен n -ой степени, a, β – числа. Рекомендуется за 
принять многочлен , т.е. 
= 
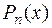, а за 
принять все, что осталось после выделения u.
2. 
Интегралы вида 
3. Интегралы вида 
, где a, β, b – числа.
В этом случае повторное применение формулы интегрирования по частям приводит к уравнению относительно искомого интервала.
Пример 3. Вычислить интегралы: а) 
; б) 
;
в) 
.
Решение. а) 
.
Так как неопределенный интеграл содержит одну произвольную постоянную, то при нахождении функции 
по ее известному дифференциалу 
(интегрированием) можно брать одну первообразную (С = 0).
б) 
= 
.
в) 
.
Возникший интеграл не является табличным, однако видно, что по сравнению с исходным интегралом степень переменной х в подынтегральном выражении уменьшилась на единицу, при этом второй сомножитель cos3 x того же типа, что и в исходном интеграле. Повторное применение формулы интегрирования по частям приводит к табличному интегралу. Действительно, положим теперь 
. Тогда 
; 
и 
.
