ДИФФЕРЕНЦИРУЕМОСТЬ ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ
ПЛАН
1. Полный дифференциал функции двух переменных.
2. Необходимое и достаточное условия дифференцируемости функции двух переменных.
3. Производная по направлению Градиент.
4. Частные производные и полные дифференциалы высших порядков.
1. Пусть функция z = f(х, у) определена в некоторой окрестности точки М (х, у). Составим полное приращение функции в точке М:
∆ z = f(x + ∆x, y + ∆у) – f(х, у).
Определение. Функция z = f(х, у) называется дифференцируемой (т.е.
имеет полный дифференциал) в точке М(х, у), если её
полное приращение можно представить в виде:
∆z = A · ∆x + B · ∆y + α · ∆x + β · ∆y, (1)
где α = α(∆х, ∆у) → 0 и β = β(∆х, ∆у) → 0 при ∆х → 0, ∆у → 0.
Сумма первых двух слагаемых в равенстве (1) есть выражение, линейное относительно ∆х и ∆у и представляет собой главную часть приращения функции. Сумма двух последних слагаемых правой части равенства (1) является бесконечно малой высшего порядка относительно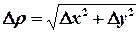 
, т.е. 
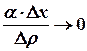или 
.
Определение. Главная часть полного приращения функции z = f(х, у),
линейная относительно ∆х и ∆у, называется полным
дифференциалом этой функции и обозначается симво-
лом dz:
dz = А · ∆х + В · ∆у. (2)
Выражения А · ∆х и В · ∆у называют частными дифференциалами.
Для независимых переменных ∆х = dх и ∆у = dу.
Поэтому равенство (2) можно записать в виде:
dz = А · dх + В · dу. (3)
Необходимое и достаточное условия дифференцируемости
Функции двух переменных.
Теорема 1 (необходимое условие дифференцируемости функции).
Если функция z = f(х, у ) имеет в точке М(х, у) полный дифферен-
циал, то она имеет в этой точке частные производные и при этом
.
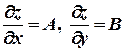Формула (3) принимает вид:
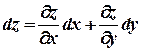. (4)
Теорема 2 (достаточное условие дифференцируемости функции).
Если функция z = f(х, у) имеет в точке непрерывные частные произ-
водные 
и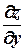 
, то она дифференцируема в этой точке и её пол-
ный дифференциал выражается формулой (4).
Правила и формулы вычисления дифференциалов функции одной переменной справедливы и для дифференциалов функции двух (и большего числа) переменных.
Производная по направлению. Градиент.
Пусть функция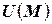 
, где точка М=(x,y) непрерывна и имеет непрерывные частные производные по двум переменным. Пусть задан вектор 
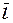(определено направление 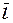). Рассмотрим точку 
, лежащую на 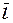, и точку 
также расположенную на 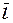. Функция 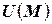при перемещении М в положение 
получит приращение
.
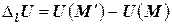Обозначим через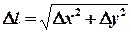 
.
Предел
называют производной функции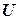 
по направлению 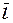и обозначают 
.
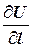ТЕОРЕМА (о вычислении производной функции по заданному направлению)
Если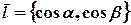 
и функция 
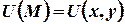непрерывна вместе со своими частными производными, тогда справедливо равенство:
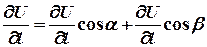. (5)
Заметим, что частные производные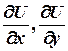 
являются частным случаем производной по направлению.
Производная 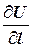характеризует скорость изменения функции 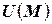по направлению вектора .
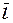Определение. Пусть задана функция 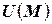в области 
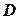. Вектор
называют градиентом функции .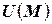
ТЕОРЕМА (о связи градиента с производной по направлению).
Пусть задана функция 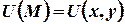. Производная 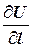по направлению некоторого вектора 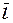равна проекции вектора 
на вектор 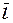, то есть 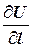можно вычислить по формуле
= 
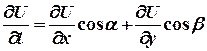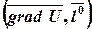. (6)
В правой части формулы (6) стоит скалярное произведение двух векторов: вектора и единичного вектора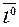 
заданного направления .
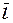Как известно из курса аналитической геометрии, единичный вектор вектора 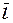можно найти по формуле
. (7)
Координатами единичного вектора 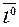являются направляющие косинусы заданного направления 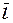, т.е. 
.
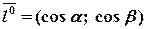