Знакочередующийся ряд можно записать в виде:
где 
Признак сходимости знакочередующегося ряда (признак Лейбница). Знакочередующийся ряд сходится, если абсолютные величины его членов монотонно убывают, а общий член стремится к нулю, т.е. если выполняется следующие два условия: 1) 
и 
.
Возьмем п -ю частичную сумму сходящегося знакочередующегося ряда, для которого выполняется признак Лейбница
пусть 
-й остаток ряда. Его можно записать как разность между суммой ряда S и п -й частичной суммой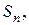 
т.е.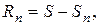 
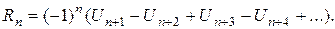
Величина 
оценивается с помощью неравенства 
Знакопеременный ряд
сходится, если сходится ряд
В этом случае исходный ряд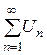 
называется абсолютно сходящимся. Сходящийся ряд 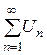называется условно сходящимся, если ряд 
расходится.
Т.к. 2 > 1, то ряд расходится.
Пример. Исследовать сходимость ряда
Решение: Применим признак Лейбница. Так как
то 
Следовательно, выполнено первое условие признака Лейбница. Так как
то выполняется и второе условие. Значит, данный ряд сходится.
Пример. Исследовать сходимость ряда
Решение: Составим ряд из абсолютных величин
Этот ряд бесконечно убывающая геометрическая прогрессия п, следовательно, данный ряд сходится, причем абсолютно.
4. Функциональные ряды.
Ряд 
члены которого – функции от х, называются функциональным. Совокупность значений х, при которых функции 
определены и ряд 
сходится, называют областями сходимости функционального ряда. Каждому значению из области сходимости Х соответствует определенное значение величины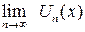 
.Эту величину называют суммой функционального ряда и обозначают через S(x).
Функциональный ряд вида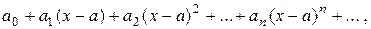 
где 
- действительные числа, называется степенным.
Основное свойство степенных рядов состоит в том, что если степенной ряд сходится при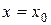 
, то он сходится (и притом абсолютно) при всяком значении х, удовлетворяющем неравенству 
(теорема Абеля).
Одним из следствий теорем Абеля является факт существования для всякого степенного ряда интервала сходимости 
, или 
с центром в точке 
, внутри которого степенной ряд абсолютно сходится и вне которого он расходится. На концах интервала сходимости (в точках 
) различные степенные ряды ведут себя по-разному: одни сходятся абсолютно на обоих концах, другие - либо условно сходятся на обоих концах, либо на одном из них условно сходятся, на другом расходятся, третьи – расходятся на обоих концах.
Число R называется радиусом сходимости степенного ряда. В частных случаях радиус сходимости ряда R может быть равен нулю или бесконечности.
Для отыскания интервала и радиуса сходимости степенного ряда можно пользоваться одним из следующих способов.
1 способ. Если среди коэффициентов ряда 
нет равных нулю, т.е. ряд содержит все целые положительные степени разности х-а, то
(3)
при условии, что этот предел (конечный или бесконечный) существует.
2 способ. Если исходный ряд имеет вид
(где р- целое положительное число: 2,3,…), то
(4)
3 способ. Если среди коэффициентов ряда есть равные нулю и последовательность оставшихся в ряде показателей степенной разности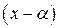 
любая, то
(5)
где 
- коэффициенты, отличные от нуля.
4. способ. Во всех случаях интервал сходимости ряда можно находить, применяя непосредственно признак Даламбера или признак Коши ряду, составленному из абсолютных величин членов исходного ряда.
Степенные ряды обладают следующим свойством: ряды, полученные почленным дифференцированием и интегрированием степенного ряда, имеют тот же интервал сходимости и их сумма внутри интервала сходимости равны соответственно производной и интегралу от суммы первоначального ряда. Если
, то
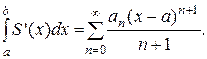
где – R<x-a<R.
Операцию почленного дифференцирования и интегрирования можно произвести над степенным рядом сколько угодно раз.
Пример. Исследовать сходимость ряда
Решение: Ряд является геометрической прогрессией со знаменателем q= 
. Он сходится, если 
и расходится, если 
. Следовательно, промежуток сходимости ряда определяется двойным неравенством 
. Там же результат можно получить, используя формулы (4), (5).
Пример. Исследовать сходимость ряда
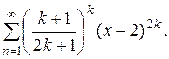
Решение: В данном случае имеем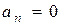 
при п=2k-1 и 
при п=2k. Для отыскания радиуса сходимости удобнее всего использовать формулу (5).
Исследуем ряд на концах интеграла сходимости. Полагая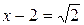 
, получаем числовой ряд
Но 
Таким образом, при х -2 
. Итак, область сходимости данного ряда 
Пример. Исследовать сходимость ряда
Решение: Применим признак Коши, полагая
получаем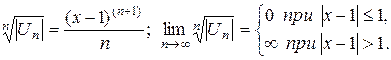 
Таким образом, ряд сходится, если 
, т.е. 
Пример. Исследовать сходимость ряда
Решение: Применяем признак Даламбера, полагая
полагаем
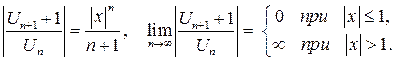
ряд сходится, если 
, т.е. 
5. Разложение функций в степенные ряды.
Ряд Тейлора. Ряд Маклорена.
Всякая функция, бесконечно дифференцируемая в интервал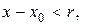е 
т.е. 
, может быть разложена в этом интервале в сходящийся к ней степенной ряд Тейлора
если в этом интервале выполняется условие
где 
- остаточный член формулы Тейлора (или остаток ряда),
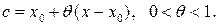
При 
получается степенной ряд Маклорена:
Если в некотором интервале, содержащем точку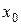 
, при любом п выполняется неравенство 
, где М – положительная постоянная, то 
и функция f(x) разложима в ряд Тейлора.
Разложение элементарных функций в ряд Маклорена.
;
;
;
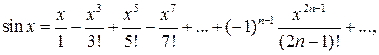
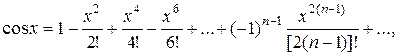
Это последнее разложение имеет место
при 
при 
при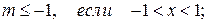 
;
.
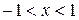Пример. Разложить в ряд по степеням х функцию 
Решение: Найдем значения функции и её производных при х =0.
, 
,
, 
, 
Так как 0 < ln 2<1, то при фиксированном х имеет место неравенство 
для любого п. Следовательно, функция может быть представлена в виде суммы ряда Маклорена:
,
поэтому
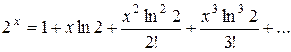
Пример. Разложить в ряд по степеням х функцию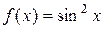 
Решение: Продифференцируем функцию п +1 раз:
,
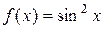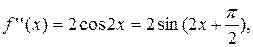
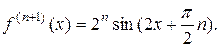
В точке х = 0 находим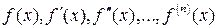 
, а значение f(n+1) (х) определяем в точке х=с. Получаем f(0)=0, 
, 
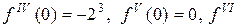
Находим остаточный член:
Так как 
при любом х, а 
величина ограниченная, то . Следовательно, функцию 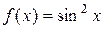можно представить в виде суммы ряда Маклорена
.
Пример. Разложить 
в ряд по степеням х.
Решение: B разложении
.
Заменим х на –х2; получим
.
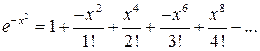
Пример. Разложить lnx в ряд по степеням х -1
Решение: B разложении
.
Заменим х на х - 1; получим
.
Пример. Разложить в ряд по степеням х -2 функцию 1/ х.
Решение: Воспользуемся равенством 
. Правую часть этого равенства можно рассматривать как сумму бесконечно убывающей геометрической прогрессии с первым членом 
и знаменателем 
Отсюда получаем
то есть
так как 
.
