Интегрирование функций, содержащих квадратный трехчлен
1. 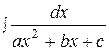 . 2.
. 2. 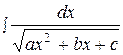 . 3.
. 3. 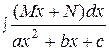 . 4.
. 4. 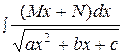 .
.
В качестве общей рекомендации при интегрировании выражений содержащий квадратный трехчлен 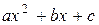 , можно указать на целесообразность применения к нему подстановки
, можно указать на целесообразность применения к нему подстановки 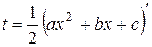 .
.
В результате интеграл приводится к сумме двух табличных интегралов.
Пример 3. Вычислить интегралы: а) 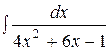 ; б)
; б) 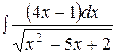 .
.
а) 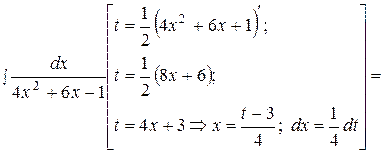
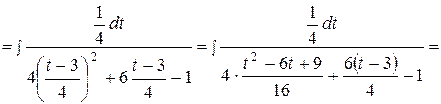
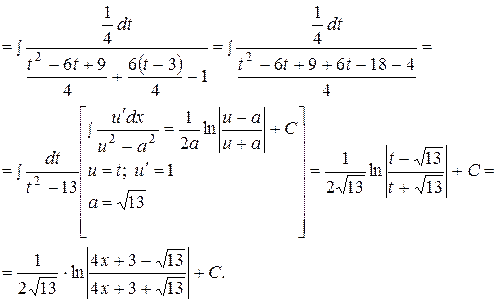
б) 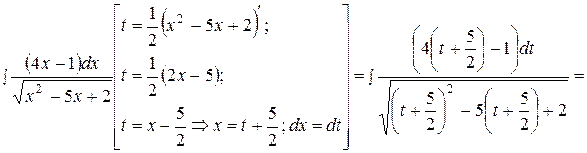
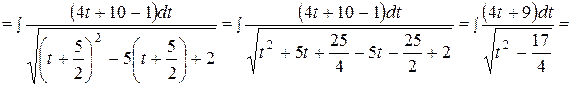
= 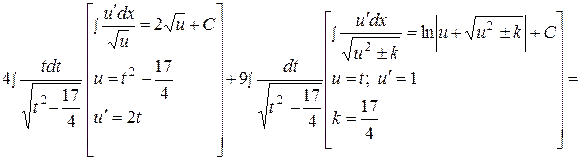
= 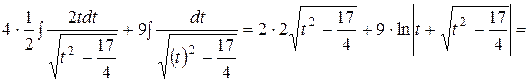
= 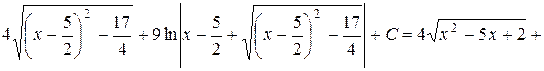
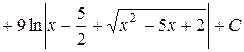 .
.
Интегрирование простейших иррациональных функций
Пусть функция зависит от двух переменных 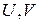 некоторых постоянных. Тогда она называется рациональной функцией переменных, если над ними производятся только операции сложения, вычитания умножения и деления. При этом рациональную функцию принято обозначать
некоторых постоянных. Тогда она называется рациональной функцией переменных, если над ними производятся только операции сложения, вычитания умножения и деления. При этом рациональную функцию принято обозначать 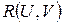 . Например,
. Например, 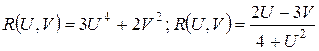 и т.д.
и т.д.
Некоторые типы интегралов от алгебраических иррациональностей надлежащий заменой могут быть сведены к интегралом от рациональных функций.
1. Если под знаком интеграла стоит рациональная функция от дробных степеней независимой переменной х, т.е. функция 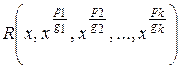 , то применяется подстановка
, то применяется подстановка 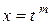 , где m – наименьшее общее кратное чисел
, где m – наименьшее общее кратное чисел 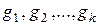 .
.
2. Если под знаком интеграла стоит функция вида 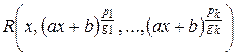 , то применяется подстановка
, то применяется подстановка 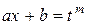 , где m – наименьшее общее кратное (Н.О.К.) чисел
, где m – наименьшее общее кратное (Н.О.К.) чисел 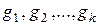 .
.
3. Если под знаком интеграла стоит рациональная функция от х и дробных степеней дробно-линейной функции, т.е. функция вида 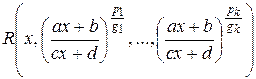 то применяется подстановка
то применяется подстановка 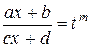 , где
, где 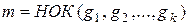 .
.
Пример 4. Вычислить интеграл: 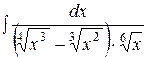 .
.
Решение. 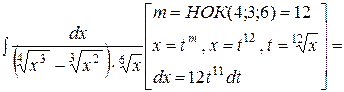

= 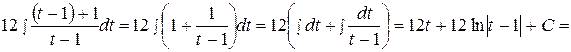
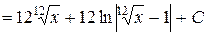 .
.
Интегрирование дробно-рациональных функций
Определение. Дробно-рациональной функцией (рациональной дробью)
называется отношение двух многочленов
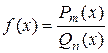
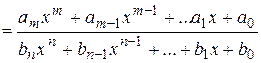 .
.
Если степень многочлена, стоящего в числителе дроби не меньше, чем степень многочлена в знаменателе, то в этой дроби следует выделить целую часть, т.е. представить ее в виде 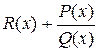 , где
, где 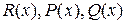 - многочлены, причем степень
- многочлены, причем степень 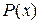 меньше степени
меньше степени 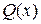 .
.
Рациональная дробь 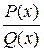 , обладающая этим свойством, называется правильной, в противном случае дробь называется неправильной.
, обладающая этим свойством, называется правильной, в противном случае дробь называется неправильной.
Например, 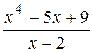 - неправильная рациональная дробь. Разделим числитель на знаменатель «уголком»:
- неправильная рациональная дробь. Разделим числитель на знаменатель «уголком»:


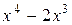
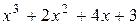 (целая часть)
(целая часть)

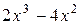
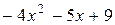
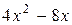
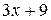
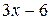
15 (остаток)
Следовательно, 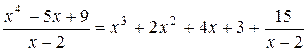 .
.
Таким образом, неправильную рациональную дробь можно единственным образом путем деления числителя на знаменатель представить в виде суммы целой части (многочлена) и правильной рациональной дроби.
Справедлива следующая теорема.
Теорема. Всякую правильную рациональную дробь можно единственным
образом представить в виде суммы простейших дробей следую-
щих 4 типов: 1) 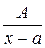 , 2)
, 2) 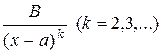 , 3)
, 3) 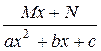 ,
,
4)  , где А, В, M, N, C, D, a, b, c – дейст-
, где А, В, M, N, C, D, a, b, c – дейст-
вительные числа, а квадратный трехчлен 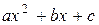 не имеет
не имеет
действительных корней (D = b 2 – 4 ас < 0).
Если знаменатель правильной рациональной дроби 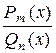 разложен
разложен
на множители 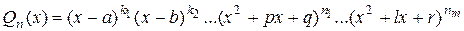 , то правильная рациональная дробь может быть единственным образом разложена на сумму простейших дробей:
, то правильная рациональная дробь может быть единственным образом разложена на сумму простейших дробей:
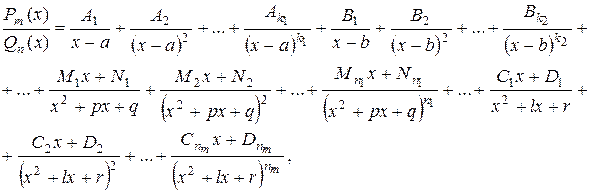
где 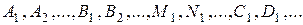 - некоторые действительные числа. Для нахождения неизвестных коэффициентов
- некоторые действительные числа. Для нахождения неизвестных коэффициентов 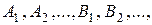
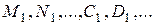 можно применить либо метод неопределенных коэффициентов, либо метод частных значений, либо их комбинацию.
можно применить либо метод неопределенных коэффициентов, либо метод частных значений, либо их комбинацию.
Пример 5. Представить дробь в виде суммы простейших дробей:
а) 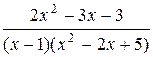 ; б)
; б) 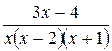 .
.
Решение. а) Так как квадратный трехчлен, стоящий в знаменателе 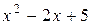 не имеет действительных корней
не имеет действительных корней 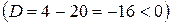 , то представим данную дробь в виде суммы простейших дробей:
, то представим данную дробь в виде суммы простейших дробей: 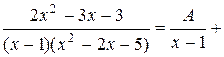
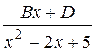 . Для нахождения неизвестных коэффициентов А, В, D, приведем дроби, стоящие в правой части уравнения к общему знаменателю и приравняем числители:
. Для нахождения неизвестных коэффициентов А, В, D, приведем дроби, стоящие в правой части уравнения к общему знаменателю и приравняем числители: 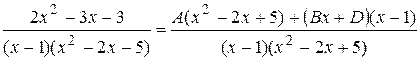 ,
, 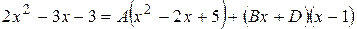 или
или
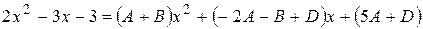 .
.
Метод неопределенных коэффициентов состоит в сравнении коэффициентов при одинаковых степенях х у многочленов, стоящих в левой и правой частей равенства, которые должны быть равны между собой:
при 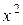 :
: 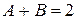 , при х 1:
, при х 1: 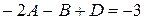 , при
, при 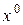 :
: 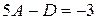 .
.
Решая систему 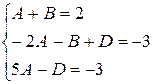 находим, что
находим, что 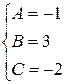 .
.
Следовательно, 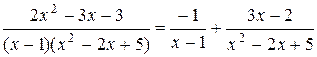 .
.
б) Имеем 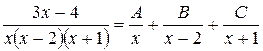 .
.
Отсюда следует, что 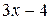
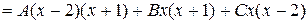 .
.
Для нахождения неопределенных коэффициентов А, В, С применим метод частных значений. Для этого вместо аргумента х подставим в полученное равенство значения корней знаменателя. Корни знаменателя: х = 0, х = 2, х = -1.
Положим х = 0, тогда – 4 = –2А, т.е. А = 2;
положим х = 2, тогда 2 = 6 В, т.е. 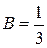 ;
;
положим х = -1, тогда – 7 = 3 С, т.е. 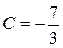 .
.
Следовательно, 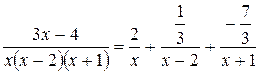 .
.






