Если криволинейная трапеция ограничена кривой, заданной параметрически  , прямыми
, прямыми  и
и  и осью Ох, то ее площадь находится по формуле:
и осью Ох, то ее площадь находится по формуле:
 , (43)
, (43)
где  и
и  определяются из равенств
определяются из равенств  и
и  .
.
 Пример 15. Найти площадь фигуры,
Пример 15. Найти площадь фигуры,
ограниченной эллипсом  .
.
Решение. Найдем сначала  площади S.
площади S.
Здесь х изменяется от 0 до а, следовательно,
t изменяется от 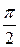 до 0 (рисунок 22).
до 0 (рисунок 22).
По формуле (43) находим Рисунок 22

 . Таким образом,
. Таким образом,  . Значит,
. Значит,  (ед2.).
(ед2.).
Вычисление объемов тел
А) Вычисление объема тела по известным площадям параллельных сечений.
Пусть имеется некоторое тело Т. Предположим, что известна площадь любого сечения этого тела плоскостью, перпендикулярной к оси Ох (рисунок 23).

Рисунок 23
Эта площадь будет зависеть от положения секущей плоскости, т.е. будет функцией от х:  , где
, где  .
.
Предположим, что  - непрерывная функция и определим объем данного тела. Проведем плоскости
- непрерывная функция и определим объем данного тела. Проведем плоскости  . Эти плоскости разобьют тело на слои. В каждом частичном отрезке
. Эти плоскости разобьют тело на слои. В каждом частичном отрезке  выберем произвольную точку
выберем произвольную точку  и для каждого значения
и для каждого значения  построим цилиндрическое тело, образующая которого представляет собой контур сечения тела Т плоскостью
построим цилиндрическое тело, образующая которого представляет собой контур сечения тела Т плоскостью  . Объем такого элементарного цилиндра с площадью основания
. Объем такого элементарного цилиндра с площадью основания 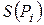 и высотой
и высотой  равен
равен 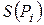
 , объем всех цилиндров будет
, объем всех цилиндров будет
 .
.
Предел этой суммы при  , где
, где  (если он существует) называется объемом данного тела:
(если он существует) называется объемом данного тела:  .
.
Так как 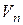 представляет собой, очевидно, интегральную сумму для непрерывной функции
представляет собой, очевидно, интегральную сумму для непрерывной функции  на
на 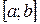 , то указанный предел существует и выражается определенным интегралом:
, то указанный предел существует и выражается определенным интегралом:
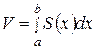 . (44)
. (44)
Формулу (44) называют формулой объема тела по известной площади поперечного сечения.
Б) Объем тела вращения.
Пусть вокруг оси Ох вращается криволинейная трапеция, ограниченная непрерывной линией 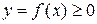 , отрезком
, отрезком 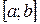 оси Ох и прямыми
оси Ох и прямыми  и
и  (рисунок 24).
(рисунок 24).
Полученная от вращения фигура называется телом вращения. Сечение этого тела плоскостью, перпендикулярной оси Ох, проведенной через произвольную точку х оси Ох  , есть круг с радиусом
, есть круг с радиусом 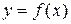 .
.
Следовательно,  . Применяя формулу (44) объема тела по площади параллельных сечений, получаем
. Применяя формулу (44) объема тела по площади параллельных сечений, получаем
 . (45)
. (45)
Если криволинейная трапеция ограничена графиком непрерывной функции 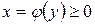 и прямыми
и прямыми 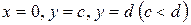 , то объем тела, образованного вращением этой трапеции вокруг оси Оу (рисунок 25) по аналогии с формулой (45), равен
, то объем тела, образованного вращением этой трапеции вокруг оси Оу (рисунок 25) по аналогии с формулой (45), равен
 . (46)
. (46)


Рисунок 24 Рисунок 25
 Пример 16. Вычислить объем тела,
Пример 16. Вычислить объем тела,
которое получается при вращении
вокруг оси Ох криволинейной тра-
пеции, ограниченной гиперболой
 , прямыми
, прямыми 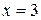 , х = 12 и
, х = 12 и
осью абсцисс.
Решение. Построим фигуру,
ограниченную заданными ли-
ниями, а затем тело вращения
вокруг оси Ох (рисунок 26). Рисунок 26
По формуле (45) имеем 

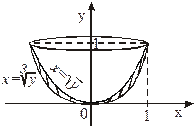
 (ед3.).
(ед3.).
Пример 17. Найти объем тела, полученного
от вращения вокруг оси ординат плоской
фигуры, ограниченной линиями 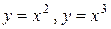 .
.
Решение. Проецируя вращаемую фигуру
на ось ординат (рисунок 27), убеждаемся, Рисунок 27
что искомый объем равен  .
.

 ;
; 
 . Следовательно,
. Следовательно,  (ед3.).
(ед3.).
Работа переменной силы.
Пусть материальная точка перемещается под действием силы  , на прямой вдоль оси
, на прямой вдоль оси  и имеет переменную величину
и имеет переменную величину 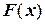 . Требуется найти работу
. Требуется найти работу  , совершаемую силой
, совершаемую силой  , по перемещению точки вдоль оси
, по перемещению точки вдоль оси  из точки
из точки  до точки
до точки  .
.
 Разобьем
Разобьем  точками. Выберем
точками. Выберем  .
.
Сила  меняется от точки к точке. Но если
меняется от точки к точке. Но если  мало, можно считать
мало, можно считать 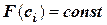 при
при  . Тогда
. Тогда  .
.
Рисунок 28
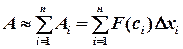 ,
, 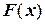 -непрерывная функция на
-непрерывная функция на  , следовательно:
, следовательно:
 .
.




