Общая схема построения модели

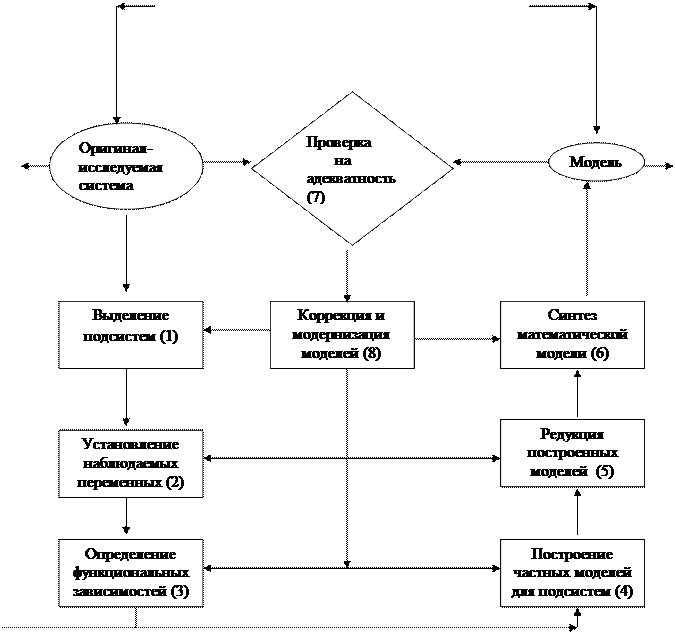
Схема устроена так, что предполагает не один итерационный цикл процесса моделирования: после i-го шага, приведшего к появлению j- ой версии модели, осуществляется очередная проверка на адекватность, после которой происходит как коррекция и модернизация модельной версии, так и возникают задания на дополнительные социологические исследования, что-то уточняющие как в модельной концепции, так и в самих этапах-процедурах моделирования. Так происходит до тех пор, пока модель не начнет выдавать полезные результаты.

Вы уже наверное заметили, насколько удобен и понятен язык схем. Абстрагирование и обобщенное его развитие получило в теории графов – математическом языке, как показал опыт, наиболее просто и быстро осваиваемом гуманитариями. Естественно начать осваивать языки моделирования именно с него.

2. Преимущество языка теоретико-графовых моделей

Как было сформулировано в разделе «Свойства моделей живых систем», одним из их специфических свойств является многомерность. К сожалению, и по настоящий момент работа математика с размерностью выше 3-х превращается в «проклятье размерностей». Однако имеется ветвь математики, в которой существует (правда, определенной ценой, но …«чудес не бывает») возможность преодолевать «проклятье размерностей». Этой ветвью является теория графов, а ключевой теоремой в этой проблеме является теорема о возможности представлении графа, построенного в любом n-мерном пространстве, в 3-х мерном пространстве.

Теорема: Любой конечный граф, построенный в многомерном пространстве с числом измерений более 3-х, может быть взаимнооднозначно отображен на граф в 3-х мерном пространстве.

Доказательство.

Пусть в пространстве N – измерений имеется многомерный конечный граф, т.е. с конечным числом n- вершин и конечным множеством m ребер. Выберем в 3-х мерном пространстве какую-то прямую, например, совпадающую с осью Z в трех мерной декартовой системе координат. Поскольку число вершин конечно, то сопоставим каждой из n вершин многомерного графа одну и только одну точку на выбранной прямой. Таким образом, их также окажется n штук.

Каждое ребро многомерного графа соединяет одну и только одну пару его вершин.

Будем поступать следующим образом, перебирая все возможные пары вершин многомерного графа: как только обнаруживается, что какая-то пара его вершин соединена ребром, то через соответствующую им пару точек на прямой, совпадающей с осью Z в 3-х пространстве, будет проводиться одна и только одна, не совпадающая с другими, плоскость. Поскольку в силу конечности графа число ребер его конечно, то и соответствующих им плоскостей также будет конечное множество.

Образно говоря, многомерному графу из n вершин и m ребер будет сопоставлена книга из m страниц и n буковок на «книжном корешке» в 3-х. мерном пространстве.

Теория графов имеет самое неожиданное применение, достаточно назвать выбор оптимальных маршрутов и потоков в сетях, моделирование жизне­деятельности организмов, исследование случайных процессов и многие другие задачи. Теория графов тесно связана с такими разделами математи­ки, как теория множеств, теория матриц, математическая логика и теория вероятностей. Во всех этих разделах графы применяют для представления различных математических объектов, и в то же время сама теория графов широко использует аппарат родственных разделов математики.

Ориентированные графы. Часто связи между объектами характе­ризуются вполне определенной ориентацией. Например, на некоторых улицах допускается только одностороннее автомобильное движение, от­ношения между людьми могут определяться подчиненностью или стар­шинством. Ориентированные связи характеризуют переход системы из одного состояния в другое, результаты встреч между командами в спор­тивных состязаниях, различные отношения между числами (неравенство, делимость). Для указания направления связи между вершинами графа соответствующее ребро отмечается стрелкой. Ориентированное таким образом ребро называют дугой, а граф с ориентированными ребрами — ориентированным графом.

Взвешенные графы. Дальнейшее обобщение отображения связей между объектами с помощью графов состоит в приписывании ребрам и дугам некоторых количественных значений, качественных признаков или характерных свойств, называемых весами. В простейшем случае это может быть порядковая нумерация ребер и дуг, указывающая на очередность при их рассмотрении (приоритет или иерархия). Вес ребра или дуги может оз­начать длину (пути сообщения), количество набранных очков (турниры), характер отношений между людьми (сын, брат, отец, подчиненный, учи­тель) и т.п. Вес можно приписывать не только ребрам и дугам, но и верши­нам. Например, вершины, соответствующие населенным пунктам на карте автомобильных дорог, могут характеризоваться количеством мест в кем­пингах, пропускной способностью станций техобслуживания. Вообще, вес вершины означает любую характеристику соответствующего ей объекта (цвет изображаемого вершиной предмета, возраст человека и т. п.).

Типы конечных графов. Если множество вершин графа конечно, то он называется конечным графом. Для ориентированного ребра (дуги) различают начальную вершину, из которой дуга исходит, и конечную вершину, в которую дуга заходит. Ребро, граничными вершинами которо­го является одна и та же вершина, называется петлей. Ребра с одинако­выми граничными вершинами являются параллельными и называются кратными. В общем случае граф может содержать и изолированные вер­шины, которые не являются концами ребер и не связаны ни между собой. ни с другими вершинами.

Маршруты. Нередко задачи на графах требуют выделения различ­ных маршрутов, обладающих определенными свойствами и характери­стиками. Маршрут длины т определяется как последовательность т ре­бер графа (не обязательно различных) таких, что граничные вершины двух соседних ребер совпадают. Замкнутый маршрут приводит в ту же вершину, из которой он начался. Маршрут, все ребра которого различны, называется цепью, а марш­рут, для которого различны все вершины, на­зывается простой цепью. Замкну­тая цепь называется циклом, а простая цепь — простым циклом. Маршрут, не содержащий повторяющихся дуг, называется путем, а не содержащий повторяющихся вершин, — про­стым путем. Замкнутый путь называется контуром, а простой замкну­тый путь — простым контуром. Граф называется циклическим (контур­ным), если он содержит хотя бы один цикл (контур).

Деревья и лес. Особый интерес пред­ставляют связные ацик­лические гра­фы, назы­ваемые деревьями. Дере­во на множестве р вер­шин всегда содержит q=p-l ребер, т.е. мини­мальное количество ре­бер, необходимое для того, чтобы граф был связным. Действительно, две вершины связываются одним ребром

и для связи каждой последующей вершины с предыдущи­ми требуется ребро, следовательно, для связи р вершин необходимо и достаточно р-1 ребер. При добавлении в дерево ребра образуется цикл, а при удалении хотя бы одного ребра дерево распадается на компоненты, каждая из которой представляет собой также дерево или изолированную вершину. (несвязный граф, компоненты которого являются деревьями, называется л есом.

Примерами древовидной структуры являются генеалогический граф (родословное дерево), а также совокупность всех файлов, размещенных на жестком диске компьютера или дискете. Каждый логический диск имеет каталог, называемый главным или корневым. Он имеет оглавле­ние, подобное оглавлению книги. В оглавлении корневого каталога пере­числено содержимое диска: имена файлов этого каталога и других ката­логов, вложенных в него.