Резонансное усиление сигналов и умножение частоты

МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ГРАЖДАНСКОЙ АВИАЦИИ

ИРКУТСКИЙ ФИЛИАЛ

 

КАФЕДРА АРЭО

 

ЛЕКЦИЯ № 4

по дисциплине

Радиотехнические цепи и сигналы

 

для студентов специальности 160905-ЗО

 

 

Раздел 4. Преобразование сигналов в нелинейных
радиотехнических цепях

Иркутск, 2013 г.

1. Нелинейные элементы и их характеристики. Способы
аппроксимации характеристик нелинейных элементов

В общем случае нелинейная цепь описывается оператором преобразования W_нц:

u_вых(t) = W_нц[U_вх(t),t], (1.1)

для которого свойство линейности не выполняется. В состав такой цепи входят один или несколько нелинейных элементов (НЭ). Различают резистивные и реактивные НЭ. В качестве резистивных НЭ выступают транзисторы, полупроводниковые диоды, электронные лампы. Примером реактивного НЭ является варикап.

При анализе НЭ предполагается, что переходные процессы в НЭ заканчиваются практически с окончанием изменения входного сигнала, т.е. НЭ является безынерционным.

В подавляющем большинстве задач радиотехники рассматриваются резистивные безынерционные НЭ. В таких элементах в качестве входного сигнала выступает напряжение, а в качестве выходного – ток, протекающий по элементу. На Рис.1.1 показаны: нелинейный двухполюсник – полупроводниковый диод и четырехполюсник, которым может быть представлен транзистор. Основной характеристикой НЭ является его вольт-амперная характеристика (ВАХ), т.е. зависимость тока, протекающего через НЭ, от приложенного к нему напряжения:

Другими характеристиками НЭ являются (Рис 1.2):

 

– статическое сопротивление или сопротивление НЭ по постоянному току:

, (1.2)

– статическая крутизна:

, (1.3)

– дифференциальное сопротивление:

, (1.4)

– дифференциальная крутизна:

. (1.5)

Статическая крутизна пропорциональна тангенсу угла α, а динамическая тангенсу угла β – угла наклона касательной ВАХ в рабочей точке.

Замена истинной (реальной) ВАХ приближенно представляющей функцией называется аппроксимацией характеристики.

Степенная аппроксимация – представление ВАХ в виде ряда Тейлора в окрестности рабочей точки (I₀, U₀):

i=f(u)=a₀+a₁(u-U₀)+a₂(u-U₀)²+… (1.6)

Кусочно-линейная аппроксимация – представление ВАХ отрезками прямых с различными наклонами. На практике ограничиваются двумя отрезками:

(1.7)

Здесь – напряжение начала характеристики; – крутизна наклона характеристики. Аппроксимации (1.6) и (1.7) показаны на Рис. 1.3.

 

2. Анализ преобразования гармонического сигнала
НЭ при степенной аппроксимации ВАХ

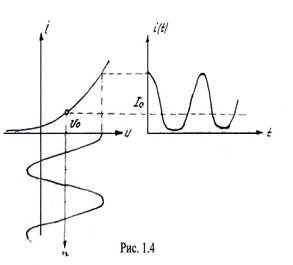На Рис. 1.4 изображены ВАХ нелинейного элемента, график входного сигнала:

u(t)=U₀+U_mcosω₀t,(1.8)

и график выходного сигнала (тока, протекающего через НЭ). Форма тока существенно отличается от формы напряжения приложенного к нему. Воспользуемся степенной аппроксимацией ВАХ, ограничившись слагаемым третьей степени. Подставляя (1.8) в (1.6) и используя тригонометрические соотношения:

,

.

получим выражение для тока, протекающего через нелинейный элемент:

i(t)=I₀+I₁cosω₀t+I₂cos2ω₀t+ I₃cos3ω₀t+…,(1.9)

где ; ; ; 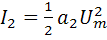(1.10)

Ток, протекающий через НЭ, содержит постоянную составляющую и совокупность гармоник, количество которых определяется наибольшей степенью аппроксимирующего полинома. При этом амплитуды четных гармоник определяются четными коэффициентами аппроксимирующего полинома, а нечетных гармоник – нечетными коэффициентами.

Анализ преобразования суммы двух гармонических сигналов при степенной аппроксимации ВАХ полиномом второй степени:

i=a₀+a₁(u-U₀)+a₂(u-U₀)². (1.11)

Входным сигналом в этом случае является колебание:

u(t)=U₀+U_m1cosω₁t+U_m2cosω₂t. (1.12)

Подстановка (1.12) в (1.11) и использование ранее приведенных тригонометрических соотношений и соотношения:

,

дает выражение для тока, протекающего через НЭ:

i(t)=I₀+I₁₁cosω₁t+I₁₂cosω₂t+I₂₁cos2ω₁t+I₂₂cos2ω₂t+

I_pcos(ω₁ – ω₂)t+ I_ccos(ω₁ + ω₂)t, (1.13)

где: ]; ; ; ; ; ;

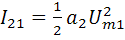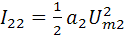. (1.14)

В этом случае ток, протекающий через НЭ содержит постоянную составляющую , гармоники кратных частот ω₁ , ω₂ , 2ω_1, 2ω₂ с амплитудами соответственно , , , 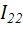и гармоники комбинационных частот: разностной частоты ω_p= ω₁ – ω₂ с амплитудой и суммарной частоты ω_с= ω₁ + ω₂ с амплитудой .

 

3. Анализ преобразования гармонического сигнала НЭ
при кусочно-линейной аппроксимации ВАХ

При кусочно-линейной аппроксимации вольт-амперная характеристика описывается выражением (1.7). Так же, как и в предыдущем случае, входной сигнал представляет собой сумму напряжения смещения U₀ и гармонического сигнала (выражение 1.8).

На Рис. 1.5 изображена вольт-амперная характеристика, а также графики входного сигнала и тока, протекающего через нелинейный элемент.

Ток, протекающий через НЭ имеет вид периодической последовательности импульсов косинусоидальной формы, ограниченных по амплитуде.

Подстановка (1.8) в (1.7) дает следующее выражение для тока:

 

(1.15)

Вводится специальный параметр – угол отсечки θ, определяемый из соотношения:

.

Откуда:

. (1.16)

В соответствии с этим величина 2θ равна длительности одного импульса, выраженного в угловой мере, т.е. ωτ_и = 2θ.

Для определения спектрального состава тока необходимо провести разложение периодической последовательности косинусоидальных импульсов в ряд Фурье, которое приводит к следующему результату:

i(t)=I₀+I₁cosω₀t+ I₂cos2ω₀t+…+ I_kcoskω₀t,

где I₀=SU_mγ₀(θ), I₁=SU_mγ₁(θ), I₂=SU_mγ₂(θ), …, I_k=SU_mγ_k(θ), – амплитуды соответствующих гармоник, γ₀(θ), γ₁(θ), γ₂(θ), …, γ_k(θ), – функции Берга.

Значения функций Берга рассчитаны для различный значений K и Θ и сведены в таблицу (табулированы).

Зависимости γ_k(θ) показывают, как изменяется амплитуда к-той гармоники тока, если амплитуда входного сигнала постоянна, а угол отсечки изменяется за счет изменения напряжения смещения .

Для получения наибольшей амплитуды желаемой гармоники тока необходимо обеспечить оптимальный угол отсечки. Так, например для второй гармоники при , оптимальный угол отсечки Θ=90⁰.

 

Резонансное усиление сигналов и умножение частоты

В технике радиопередающих устройств широко применяются резонансные усилители мощности. Их отличительная черта – работа при больших амплитудах входных напряжений, что делает обязательным учет нелинейного характера ВАХ активных элементов (транзис-торов или электронных ламп).

Схема резонансного усилителя изображена на Рис. 2.1. На вход усилителя (в цепь база – эмиттер) подается входное напряжение:

u(t)=u_c(t)+U₀=U_mвх cos ω₀t+U₀. (2.1)

Нагрузкой усилителя служит колебательный контур, настроенный на частоту сигнала, т.е. ω_p= ω₀ . ВАХ транзистора представлена отрезками прямых, т.е. имеет кусочно-линейную аппроксимацию вида 1.

На Рис. 2.2 показаны графики токов и напряжений в усилителе.

Ток, протекающий в коллекторной цепи имеет вид последовательности косинусоидальных импульсов (Рис. 2.2, а). Так как нагрузкой усилителя является контур, настроенный на частоту ω₀, ведущую роль в работе усилителя играет первая гармоника тока (Рис. 2.2, б).

Амплитуда первой гармоники тока:

I₁=SU_mвхγ₁(θ), (2.2)

Амплитуда выходного напряжения:

U_mвых=I₁R_э=SU_mвхR_э γ₁(θ), (2.3)

где .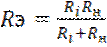

R_i – внутреннее сопротивление НЭ,

R_н = ρQ – сопротивление нагрузки,

Q – добротность контура, ρ – характеристическое сопротивление контура.

Сопротивление нагрузки на частотах 2ω₀, 3ω₀ и т.д. ничтожно мало и высшие гармоники практически не дают вклада в выходной сигнал. График выходного напряжения изображен на Рис. 2.2, в. Из этого графика следует, что:

.

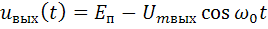Так как колебательный контур сам усиливает гармоническую составляющую частоты ω₀ (добротность контура велика), то амплитуда U_mвых достигает значений, близких к . Тогда в определенные промежутки времени выходное напряжение u_вых(t) превосходит напряжение (Рис. 2.2, в). Физически это объясняется тем, что при закрытом транзисторе потенциал коллектора определяется напряжением , с которым складывается напряжение на заряжающейся емкости (за счет запасенной в индуктивности контура энергии). Этим обусловлен эффект усиления.

Зависимость U_mвых= ƒ(U_mвх) называется колебательной характеристикой, которая должна быть линейной в диапазоне от 0 до U_mвх (Рис. 2.3). В общем случае колебательная характеристика нелинейна, так как θ (выражение 1.16), а следовательно и γ₁(θ) зависит от U_mвх. Исключение: U_н=U₀, θ=90⁰. При этом γ₁(90⁰) = 0.5, а U_mвых=0.5SU_mвхR_э.

Ширина линейного участка определяется критическим значением U_{mвх кр}. При U_mвх < U_{m кр} режим работы усилителя называют недонапряженным, а при U_mвх > U_{m кр} - перенапряженным режимом.

Если в схеме резонансного усилителя колебательный контур будет настроен

на частоту ω_k =k ω₀, то его используют в качестве умножителя частоты. При этом амплитуда выходного напряжения равна:

U_вых=I_kR_э=SU_mвхR_э γ_k(θ). (2.4)

Так как значения γ_k(θ) существенно снижаются с ростом номера k, и амплитуда выходного напряжения значительно падает, поэтому практически, как правило, реализуют удвоители и утроители частоты.

 

Преобразование частоты

Преобразование частоты или гетеродирование – это сдвиг спектра радиосигнала по оси частот на определенное постоянное значение при сохранении его структуры. Процедура преобразования частоты связана с воздействием на НЭ двух напряжений: напряжения u_с(t) радиосигнала и напряжения вспомогательного генератора u_г(t), называемого гетеродином.

При рассмотрении воздействия двух гармонических сигналов на НЭ (пункт 1.2) было показано, что в спектре тока НЭ помимо составляющих кратных частот присутствуют составляющие комбинационных частот, которые и используются при осуществлении преобразования частоты.

Принципиальная схема преобразователя частоты представлена на Рис. 2.4.

На вход преобразователя поступает сигнал:

u(t) =U_c(t)cosω₀t+U_гcosω_гt+U₀. (2.5)

где U_г, ω_г – соответственно амплитуда и частота гетеродина.

ВАХ транзистора аппроксимируется квадратичным членом степенного разложения:

I = a₂(u - U₀)². (2.6)

Подстановка (2.5) в (2.6) после преобразований с использованием выше упоминавшихся тригонометрических соотношений дает:

.(2.7)

Из этого выражения следует, что составляющие разностной частоты:

, (2.8)

и суммарной частоты:

, (2.9)

с точностью до постоянного коэффициента повторяют закон изменения амплитуды радиосигнала , но на разностной и суммарной частотах. Таким образом, спектр радиосигнала без изменения его формы оказывается сдвинутым либо в область более низких , либо в область более высоких частот. При соответствующей настройке контура будет выделено напряжение полезного сигнала на соответствующей частоте.

Если - однотональный амплитудно-модулированный сигнал:

, (2.10)

то сигнал на выходе преобразователя на разностной частоте в соответствии с (2.8) будет иметь вид:

. (2.11)

 

На Рис. 2.5 показаны спектры сигнала преобразователя при (Рис. 2.5,а) и при (Рис. 2.5,б).

Из (2.11) следует, что для увеличения амплитуды составляющих преобразованного сигнала следует выбирать .

Нелинейный элемент в составе преобразователя называется смесителем.