Методы составления характеристического уравнения

 

Свободный режим схемы не зависит от источников энергии, определяется только структурой схемы и параметрами ее элементов. Из этого следует, что корни характеристического уравнения p ₁, p ₂,…, p_n будут одинаковыми для всех переменных функций (токов и напряжений).

Характеристическое уравнение можно составить различными методами. Первый метод – классический, когда характеристическое уравнение составля­ется строго в соответствии с дифференциальным по классической схеме. При расчете переходных процессов в сложной схеме составляется система из “ m ” дифференциальных уравнений по законам Кирхгофа для схемы цепи после коммутации. Так как корни характеристического уравнения являются общими для всех переменных, то решение системы дифференциальных уравнений вы­полняется относительно любой переменной (по выбору). В результате решения получают неоднородное дифференциальное уравнение с одной переменной. Со­ставляют характеристическое уравнение в соответствии с полученным диффе­ренциальным и определяют его корни.

Пример. Составить характеристическое уравнение и определить его корни для переменных в схеме рис. 131. Параметры элементов заданы в общем виде.

 

 

 

Система дифференциальных уравнений по законам Кирхгофа:

 

Решим систему уравнений относительно переменной i ₃, в результате по­лучим неоднородное дифференциальное уравнение:

Характеристическое уравнение и его корень:

 

[c^-1]

Второй способ составления характеристического уравнения заключается в приравнивании нулю главного определителя системы уравнений Кирхгофа для свободных составляющих переменных.

Пусть свободная составляющая произвольного тока имеет вид , тогда

 

Система уравнений для свободных составляющих получается из системы дифференциальных уравнений Кирхгофа путем замены производных от пере­менных на множитель р, а интегралов – на 1 /р. Для рассматриваемого примера система уравнений для свободных составляющих имеет вид:

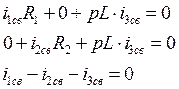
Характеристическое уравнение и его корень:

Третий способ составления характеристического уравнения (инженерный) заключается в приравнивании нулю входного операторного сопротивления схемы относительно любой ее ветви.

Операторное сопротивление элемента получается из его комплексного сопротивления путем простой замены множителя jω на р, следовательно

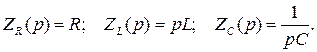
Для рассматриваемого примера:

;

;

.

Третий способ является наиболее простым и экономичным, поэтому он чаще других применяется при расчете переходных процессов в электрических цепях.

Корни характеристического уравнения характеризуют свободный пере­ходной процесс в схеме без источников энергии. Такой процесс протекает с по­терями энергии и поэтому затухает во времени. Из этого следует, что корни ха­рактеристического уравнения должны быть отрицательными или иметь отрица­тельную вещественную часть.

В общем случае порядок дифференциального уравнения, которым описы­вается переходный процесс в схеме, и, следовательно, степень характеристиче­ского уравнения и число его корней равны числу независимых начальных усло­вий, или числу независимых накопителей энергии (катушек L и конденсаторов C). Если в схеме цепи содержатся параллельно включенные конденсаторы С ₁, С ₂,… или последовательно включенные катушки L ₁, L ₂,…, то при расчете пере­ходных процессов они должны быть заменены одним эквивалентным элемен­том С _Э = С ₁ + С ₂+… или L _Э = L ₁ + L ₂+…

Таким образом, общий вид решения для любой переменной при расчете переходного процесса может быть составлен только из анализа схемы цепи, без составления и решения системы дифференциальных уравнений.

Для рассматриваемого выше примера:

а) – при e (t)= E =const;

б) – при e (t)= E_m sin(ωt + ).