Расчет электрических цепей, содержащих источники энергии [источники ЭДС e (t)и источники тока j (t)] с несинусоидальной формой кривой, выполняется по методу положения. Процедуру расчета можно условно разделить на три этапа.
1)Гармонический анализ.
На этом этапе выполняется разложение несинусоидальных функций источников ЭДС e (t)и источников тока j (t)в гармонический ряд Фурье:
Для проведения анализа структуры функций e (t) и j (t)количество гармоник в их разложении определяютзначительно больше, чем необходимо для расчета схемы.
2)Аналитический расчет.
Производится аналитический расчет схемы последовательно для каждой гармоники в отдельности. Для постоянной составляющей расчет производится как для резистивной цепи постоянного тока, при этом участки с катушками L закорачиваются, а ветви с конденсаторами C размыкается. Расчет схемы для отдельных гармоник производится как для цепи синусоидального тока, т.е. в комплексной форме, при этом определяются не действующие значения, а комплексные амплитуды токов и напряжений (
). Расчет для каждой гармоники выполняется по одному и тому же алгоритму, при этом учитывается зависимость реактивных сопротивлений элементов от частоты и, следовательно, от номера гармоники: 
. Выбор расчетного метода определяется структурой расчетной схемы.
Количество гармоник, для которых выполняется расчет схемы, устанавливается исходя из конкретных условий задачи. Например, если определяются только действующие значения токов и напряжений (I, U), то достаточно учитывать только те гармоники, для которых коэффициент 
, при этом относительная погрешность расчета в итоге не превысит 1%. Однако в тех случаях, когда требуется проводить исследование форм кривых функций u (t) и i (t), то необходимо учитывать также гармоники более высокого порядка с меньшим коэффициентом гармоник 
.
3.Синтез решения.
На заключительной стадии расчета определяются искомые величины согласно условию задачи.
Мгновенные значения токов и напряжений i (t)и u (t) определяются в соответствии с принципом наложения как алгебраической суммы мгновенных значений отдельных составляющих, например:
При необходимости исследования формы кривых функций i (t) и u (t) по полученным уравнениям строится их графические диаграммы.
Действующие значения токов и напряжений (I, U) находятся как среднеквадратичные значения этих функций по полученным ранее формулам, например:
Активные мощности отдельных элементов определяется как суммы активных мощностей этих элементов для отдельных гармоник, например:
Активную мощность отдельных приемников можно определять также по формуле Джоуля: 
, где 
-действующее значение тока этого приемника.
Определяются коэффициенты исследуемых несинусоидальных функций: ku - коэффициент искажения, kф - коэффициент формы, kг - коэффициенты отдельных гармоник и т. д.
Пример. На входе схемы (рис. 123а) с заданными параметрами элементов (R 1=30 Ом, R 2=20 Ом, L =100 мГн, С =22 мкФ) действует источник несинусоидальной ЭДС (рис. 123б) с частотой f =50 Гц. Требуется определить 1) действующие значения ЭДС Е и токов I, I 1, I 2; 2) коэффициенты искажения функций ЭДС e (t)и токов i (t), i 1(t), i 2(t); 3) баланс активных мощностей 
.
 |
1-ый этап. Разложение заданной графически функции ЭДС е (t) (рис. 123б) в гармонический ряд Фурье производится с помощью ЭВМ по программе GAR, в результате получим:
Примечание: гармоники, кратные трем, в разложении данной функции отсутствуют.
2-ой этап. Производится расчет схемы для каждой гармоники в отдельности в комплексной форме по одному и тому же алгоритму:
; 
; 
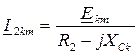, где k - номер гармоники.
Результаты расчета сведены в общую таблицу. Расчет останавливаем на 5-ой гармонике, так как амплитуды более высоких гармоник в функции e (t) незначительны и их учет уже не повлияет на конечные результаты расчета.
| k | E km | I km | I 1 km | I 2 km |
| 157,9 ej 0 | 3,081 e-j 30,4 | 3,634 e-j 46,3 | 1,080 ej 82,1 | |
| 39,5 ej 180 | 0,385 ej 180 | 0,576 ej 115,5 | 0,526 e-j 105,4 | |
| 9,9 ej 0 | 0,190 ej 45,2 | 0,077 e-j 76,54 | 0,240 ej 61,1 | |
| 6,3 ej 180 | 0,154 e-j 135,1 | 0,039 ej 100,8 | 0,179 e-j 124,6 |
3-ый этап. Определяются интегральные параметры искомых функций. Действующие значения функций:
В; I =2,20 A; I 1=2,60 A; I 3=0,88 A.
Коэффициенты искажения формы кривых для функций e (t), i (t), i 1(t), i 2(t):
; 
; 
.
Активная мощность источника энергии:
Вт.
Активная мощность приемников энергии:
Вт; 
Вт.
Баланс мощностей: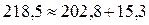 
Анализ результатов решения и выводы:
1. Для определения действующих значений величин и активных мощностей можно было бы пренебречь 4-ой и 5-ой гармониками, однако для определения коэффициентов искажения формы кривых учет названных гармоник необходим.
2. Величина и характер входного сопротивления схемы зависит от номера гармоники: для 1-ой гармоники (
) – входное сопротивление носит активно-индуктивный характер; для 2-ой гармоники (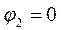
)– входное сопротивление носит чисто активный характер, т.е. на частоте 2-ой гармоники имеет место резонанс токов; для 4-ой гармоники (
)– входное сопротивление носит активно-емкостный характер.
3. Форма кривой функции тока i 1(t)в ветви с катушкой искажена меньше, чем форма кривой источника ЭДС e(t) (
), а форма кривой тока i 2(t)в ветви с конденсатором, наоборот, искажена больше (
). Такие соотношения между коэффициентами искажения форм кривых объясняются зависимостью реактивных сопротивлений от частоты: 
.
