Под активной мощностью P понимают количество энергии, потребляемое (генерируемое) объектом за единицу времени. Математически активную мощность определяют как среднее значение мгновенной мощности за полный период.
Пусть некоторый элемент цепи потребляет ток i (t) при несинусоидальном напряжении u (t):
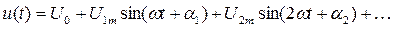
Мгновенная мощность 
, тогда активная мощность будет равна:
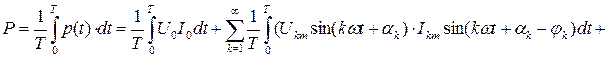
Таким образом, активная мощность несинусоидального тока равна сумме активных мощностей отдельных гармоник:
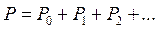
Реактивная мощность Q несинусоидального тока определяется по аналогии с активной мощностью P как алгебраическая сумма реактивных мощностей отдельных гармоник:
Как известно, реактивная мощность Q синусоидального тока характеризует интенсивность колебаний энергии (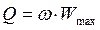
) с частотой w между электромагнитным полем элемента и остальной цепью. В цепи несинусоидального тока колебания энергии происходят на разных частотах. Сложение реактивных мощностей отдельных гармоник, характеризующих колебания энергии на разных частотах, лишено физического смысла. Математически может получиться, что реактивные мощности отдельных гармоник имеют разные знаки и в сумме дают нуль, хотя колебания энергии при этом имеют место. Таким образом, для цепи несинусоидального тока понятие реактивной мощности лишено физического смысла.
Для цепи несинусоидального тока применяется также и понятие полной мощности, которая определяется как произведение действующих значений напряжения и тока:
Как известно, для цепи синусоидального тока мощности P, Q, S образуют прямоугольный треугольник, из которого следует соотношение: 
. Для цепей несинусоидального тока это соотношение между мощностями выполняется только для резистивных элементов, в которых в соответствии с законом Ома (
) формы кривых функций u (t) и i (t) идентичны. Если в цепи содержатся реактивные элементы L и С, то это соотношение не выполняется: 
. Для баланса этого уравнения в его правую часть вносят добавление: 
, откуда
где Т - мощность искажения – понятие математическое, характеризует степень различия в формах кривых напряжение u (t)и тока i (t).
6. Коэффициенты, характеризующие несинусоидальные функции u (t), i (t)
Пусть несинусоидальная функция u (t)содержит только гармонические составляющие:
Несинусоидальные функции токов и напряжений, не содержащие постоянных составляющих (
) характеризуются следующими параметрами и коэффициентами.
Действующее значение всей функции определяется по формуле:
.
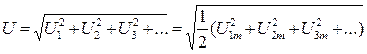Действующее значение высших гармоник:
.
Максимальные значения функции в положительной области (
) и в отрицательной области (
) не будут равны друг другу при наличии в гармоническом ряду функции четных гармоник и зависят как от амплитуд отдельных гармоник, так и от их фазовых сдвигов (начальных фаз).
Среднее по модулю значение функции определяется как среднеарифметическое значение модулей мгновенных значений функции за полный период:
.
Среднее значение функции зависит как от амплитуд отдельных гармоник, так и от их начальных фаз.
Коэффициентом амплитуды функции называется величина, равная отношению ее максимального (по модулю) значения к действующему значению:
для синусоиды.
Коэффициентом формы кривой функции называется величина, равная отношению действующего значения функции к ее среднему значению:
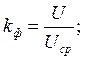
для синусоиды.
Коэффициентом k -ой гармоники называется величина, равная отношению действующего значения (амплитуды) k -ой гармоники к действующему значению (амплитуде) основной гармоники:
.
Коэффициентом искажения синусоидальности формы кривой функции называется величина, равная отношению действующего значения всех высших гармоник к действующему значению основной гармоники:
.
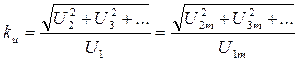Для приемников, работающих в несинусоидальном режиме, применяется понятие коэффициента мощности, который определяется как отношение активной мощности P к полной мощности S:
.
