Соответственно, количество тепла на ТS –диаграмме изохорного ТП определяется площадью под изохорой 1-2, то есть S1-2-3-4-1.
Долю поступающего (отводимого) в рабочее тело тепла, затраченного на изменение внутренней энергии Du, определим, принимая во внимание 1-й закон термодинамики:
. (7.2.10)
Следовательно, доля тепла на совершение работы деформирования будет:
. (7.2.11)
Изотермический процесс
Изотермический процесс, характеризующийся условиями T = const и dT = 0, может протекать, например, в цилиндре поршневого двигателя, в котором по мере подвода (отвода) тепла к газообразному рабочему телу поршень двигателя перемещается по такому закону, при котором объём рабочего тела увеличивается (уменьшается) настолько, что его Т остаётся неизменной.
В этом случае из уравнения Клапейрона получаем:
Из (7.4.1) видно, что объём рабочего телапри T = const изменяется обратно пропорционально его Р (закон Бойля-Мариотта). Графиком процесса является изотерма (изотерма (греч.) – линия одинаковой температуры; изо – равный, одинаковый, терм – тепло), представляющая собой на Рv - диаграмме равнобокую гиперболу, для которой координатные оси Р и v служат асимптотами (см. рис. 7.4.1).
 |
Изображение изотермического процесса на Pv-диаграмме
На графике процесс 1-2 является прямым и обеспечивается поступлением тепла в рабочее тело. Процесс же 1-3 является обратным. В этом случае рабочее тело отдаёт тепло в ОС.
Работа деформирования газообразного рабочего тела в изотермическом процессе 1-2 будет:
(7.4.2)
Принимая во внимание (7.4.1), формулу (7.4.2) можно представить в следующих видах:
На Рv - диаграмме lд в процессе 1-2 соответствует площади S1-2-4-5-1.
Располагаемая работа в изотермическом процессе 1-2 определяется как
Сравнивая (7.4.3) и (7.4.4), видим, что в изотермическом процессе располагаемая работа равна работе деформирования рабочего тела, то есть в этом процессе вся работа деформирования превращается в полезную работу. Этот факт предопределил применение изотермы в цикле Карно, который является циклом идеальной тепловой машины. Соответственно, на Рv - диаграмме l рас в процессе 1-2 соответствует площади S1-2-6-7-1.
Применительно к изотермическому процессу уравнение (5.3.7) имеет вид du = CV,удdT = 0. Нулю также равняется и изменение энтальпии рабочего тела в этом процессе di = CP,удdT= 0. Принимая во внимание первый вид дифференциального уравнения 1-го закона термодинамики, получаем:
dqТ = du + dlд = 0 + dlД = dlд.
Из данного выражения видно, что в изотермическом процессе всё подводимое (отводимое) к рабочему телу тепло затрачивается на совершение работы его деформирования.
Полученная взаимосвязь между dqТ и dlД позволяет определить изменение энтропии в изотермическом процессе:
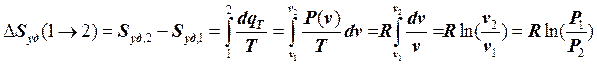.(7.4.5)
Аналогичный результат получается и при использовании для вычисления DSуд(1®2) формулы (6.4.3), так как при изотермическом процессе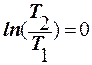 
:
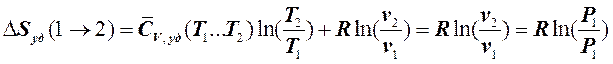
В связи с тем, что в изотермическом процессе теплоёмкость вещества равна бесконечности (см. 4.1), то определить количество тепла, подведённого (отведённого) к рабочему телу в этом процессе при помощи теплоёмкости, нельзя. Это можно сделать только через изменение энтропии в этом процессе. Используя уравнение (6.2.10) и учитывая (7.4.5), получаем:
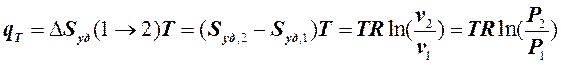. (7.4.6)
 |
Изображение изотермического процесса на TS-диаграмме
На TS -диаграмме изотермический процесс изображается горизонтальной прямой (T=const). Площадь S1-2-4-5-1 под процессом 1-2 численно равна количеству тепла, поступившему в газообразное рабочее тело из окружающей среды.
Распределение тепла между Du(Т 1 …Т 2 ) и lд соответственно будет:
и 
(7.4.7)
Адиабатный процесс
Адиабатным называется ТП изменения состояния рабочего тела рабочего телабез теплообмена с окружающей средой ОС, то есть при выполнении условий: dq = 0 и q = 0 (адиабата (греч.) - непереходимо). Условие q = 0 для адиабатного процесса является необходимым, но недостаточным. Действительно, в начале сжатия газа в цилиндре дизельного двигателя Т стенок цилиндра выше Т газа. Поэтому в этот момент тепло передаётся от стенок цилиндра сжимаемому газу. По мере сжатия газа его Т повышается настолько, что в конце сжатия стенки цилиндра оказываются уже холоднее газа. В этом случае сжатый газ начинает уже отдавать тепло стенкам цилиндра. В частном случае количество тепла, полученного газом от стенок цилиндра в начале сжатия, может оказаться равным количеству тепла, отданного газом стенкам цилиндра в конце сжатия. В этом случае суммарный теплообмен рабочего тела и ОС будет равным нулю (q = 0), хотя процесс сжатия газа был явно не адиабатным. Таким образом, необходимым и достаточным для адиабатного процесса является условие dq = 0.
Для того чтобы осуществить адиабатный процесс, следует либо рабочее тело отделить от ОС теплоизолированной (адиабатной) оболочкой, либо провести процесс настолько быстро, чтобы изменение температуры рабочего тела, обусловленное его теплообменом с ОС, было пренебрежимо мало по сравнению с изменением Т, вызванным расширением или сжатием рабочего тела. Как правило, это возможно, так как теплообмен происходит значительно медленнее, чем сжатие или расширение газа. Последние процессы имеют место в термодинамике потоков, что даёт возможность при конструировании сопел, эжекторов, инжекторов и так далее использовать основные закономерности обратимого адиабатного процесса. Адиабатные процессы имеют также большое значение и в теплотехнике. В паровых и газовых турбинах, в двигателях внутреннего сгорания и дизельных двигателях процессы расширения и сжатия газообразных рабочих тел происходят очень быстро, поэтому процессом теплообмена во многих случаях можно пренебречь.
Так как в адиабатном процессе dq = 0, то 
Отсюда следует, что в обратимом адиабатном процессе энтропия рабочего тела не изменяется, то есть Sуд = const. Поэтому обратимый адиабатный процесс очень часто в литературных источниках называют изоэнтропным процессом.
Уравнения 1-го закона термодинамики для адиабатного процесса принимают вид:
(7.5.1)
где dlд , dlрас – элементарные работы деформирования и располагаемая газообразного рабочего тела в адиабатном процессе, Дж.
Разделив нижнее уравнение на верхнее и сделав элементарные преобразования, получаем:
(7.5.2)
где k – показатель адиабаты.
Проинтегрируем последнее уравнение, при этом для расчётов, не требующих очень большой точности, рекомендуется брать k постоянным и равным его среднему значению в рассматриваемом диапазоне температур, то есть 
(далее запись 
в расчётных формулах в основном будет опущена и подразумеваться по умолчанию). Для большинства же практических расчётов можно вообще не учитывать влияние температуры на величину k, так как характер изменения CP, уд и CV, уд в поле температур у газов очень близок, что делает влияние температуры на величину k относительно небольшим. С учётом этих допущений, получаем:
Таким образом, уравнениями обратимого адиабатного процесса являются:
или 
. (7.5.4)
Уравнение (7.5.4) в технической литературе называют также уравнением Пуассона, а показатель адиабаты k коэффициентом Пуассона (не следует его путать с коэффициентом Пуассона, являющимся одним из показателей упругого деформирования твёрдых тел).
В технической литературе используются также и другие виды уравнения обратимого адиабатного процесса. Их можно легко получить из (7.5. 4), воспользовавшись уравнением Клапейрона. Имеем:
Подставив теперь в (7.5.4) P и v как функции соответственно v и P, получим:
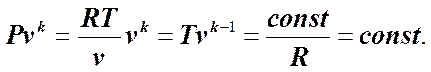
В правой части данного уравнения имеем частное от деления двух постоянных величин, которое также является постоянной величиной. Следовательно:
. (7.5.5)
Аналогично получим:
(7.5.6)
Из (7.5.3) следует, что:
и 
. (7.5.7)
Запишем уравнение Клапейрона для начала и конца процесса:
и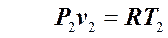 
.
Разделив почленно эти уравнения, получим:
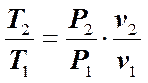. (7.5.8)
Используя (7.5.7) из (7.5.8), можно получить для адиабатного ТП соотношения между Т, v и Р:
(7.5.9)
Из (7.5.9) следует, что:
. (7.5.10)
В связи с тем, что у газов всегда k > 1, получаем, что в адиабатном процессе сжатие газообразных рабочих тел, приводящее, соответственно, к уменьшению их объёмов, имеет место увеличение Т газов, а их расширение сопровождается уменьшением Т газов.
Это широко применяется на практике. Так, если открыть вентиль баллона, в котором находится сжатый до Р » 40 ат СО2, то последний станет адиабатно расширяться. При этом его температура падает до Т » - 80 0С, и часть газа превращается в кристаллическую массу наподобие снега. Прессуя эту массу, получают, так называемый, «сухой лёд». В дизельном двигателе при быстром сжатии воздуха его температура возрастает до Т » 500…600 0С, что приводит к самовоспламенению дизельного топлива, впрыскиваемого в цилиндр в конце сжатия.
Таким образом, сжатие газов приводит к увеличению их внутренней энергии u, а расширение - к её уменьшению. Изменение внутренней энергии в адиабатном процессе определяется по известной формуле (5.3.10):
Работа деформирования, совершаемая газообразным рабочим телом над окружающей средой при равновесном адиабатном процессе, может быть вычислена по уравнению адиабаты. Учитывая (7.5.4), получим:
Учитывая это, получаем:
Учитывая (7.5.9), преобразуем (7.5.12) к виду часто используемому в технических расчётах:
Многообразие формул для расчётов величины lд позволяет в зависимости от наличия исходных данных выбирать наиболее приемлемую расчётную формулу.
Получить формулу (7.5.12) можно и несколько другим способом. При
dq = 0 первый вид уравнения 1-го закона термодинамики становится:
dlд = - du. Последнее равенство наглядно показывает, что работа расширения рабочего тела в адиабатном процессе совершается только за счёт уменьшения внутренней энергии, а его сжатие увеличивает внутреннюю энергию. После интегрирования имеем:
Учитывая (5.3.11), получаем:
(7.5.14)
Но согласно (4.5.3)
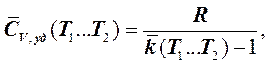
следовательно:
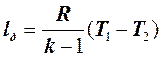. (7.5.15)
Из (7.5.14) и (7.5.15) следует, что при расширении рабочего тела (в этом случае Т 1 > Т 2) lд > 0, а при его расширении (в этом случае Т 1 < Т 2) lд < 0.
Следовательно, изменение внутренней энергии рабочего тела в адиабатном процессе может быть определено как:
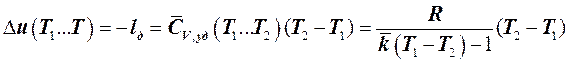. (7.5.16)
При обратимом адиабатном процессе располагаемая работа lрас будет в k раз больше (по модулю) работы деформирования, то есть lрас = k | lд |. Действительно, используя уравнение адиабаты (7.5.4), имеем:
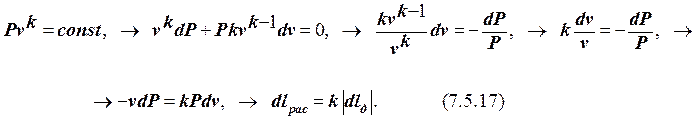
Проинтегрировав последнее уравнение, получаем, что lрас = k | lд |. Таким образом, располагаемая работа в адиабатном процессе в k раз превышает (по модулю) работу деформирования. Это обусловлено тем, что в располагаемую работу помимо работы деформирования преобразуется также и часть внутренней энергии рабочего телав количестве (k-1)lд = (k-1)Du (T 1… T 2). В этом проявляется особенность адиабатного процесса, позволяющая извлечь в качестве полезной работы также и часть внутренней энергии РТ. Это предопределило использование адиабаты в цикле Карно.
Графически работа деформирования lд и располагаемая работа lрас отображается на Pv - диаграмме (рис. 7.5.2) соответственно площадями S1-2-3-4-1 и S1-2-6-5-1.
 |
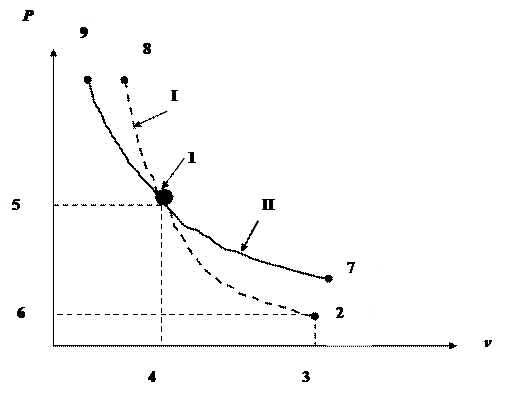Взаимное расположение адиабаты ( I) и изотермы (II)
На Pv-диаграмме
Так как k > 1,0, то на Pv - диаграмме адиабата 
идёт круче, чем изотерма 
. Давление P при адиабатном расширении Т (линия 1-2) падает быстрее, чем при изотермическом (линия 1-7), то есть адиабата расположится ниже изотермы. Это объясняется тем, что при адиабатном расширении помимо снижения Р уменьшается и Т рабочего тела. При изотермическом же расширении Т = const. Если от точки 1 рабочего телабудет сжиматься, то адиабата (линия 1-8) будет возрастать быстрее изотермы (линия
1-9), то есть адиабата расположится выше изотермы. Причиной этого является то, что при адиабатном процессе сжатия имеет место увеличение Т, что приводит к более быстрому возрастанию Р, чем это происходит при изотермическом сжатии.
Изменение энтальпии в адиабатном процессе определяется соответственно по формуле:
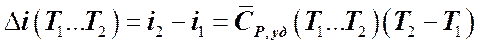. (7.5.19)
Так как в адиабатном процессе энтропия газообразного рабочего тела не изменяется, то на TS -диаграмме этот процесс изображается вертикальной прямой, при этом не надо забывать, что уменьшение Т рабочего тела происходит при его расширении (прямой процесс), а увеличение Т – при сжатии. Согласно (5.4.10), в адиабатном процессе lрас = i 1 – i 2. Следовательно, изменение энтальпии в этом процессе можно определять как:
(7.5.20)
 |
|
Изображение адиабатного процесса на TS-диаграмме
Определение распределения тепла между Du(Т 1 …Т 2 ) и lД в адиабатном процессе в принципе не имеет смысла, так как dq = 0. Действительно:
и 
(7.5.21)
Политропный процесс
Все рассмотренные выше ТП имели определённые особенности. В каждом из них на какую-либо из величин накладывались определённые ограничения: v = const, P = const, T = const, dq = 0. Реальные же ТП, как правило, протекают при наличии теплообмена и с изменением v, P, Т. Эти параметры зачастую изменяются по очень сложным зависимостям, что делает их чрезвычайно трудными для изучения. Исследования этих процессов показали, что их изучение в принципе становится возможным, если теплоёмкость газообразного рабочего теласчитать постоянной величиной в рассматриваемых температурных границах от Т 1 до Т 2 изучаемого ТП. При этом следует отметить, что при изменении температурных границ этого ТП, например, от Т¢ 1 до Т¢ 2 теплоёмкость, являясь также постоянной величиной, будет иметь уже другое численное значение. Такие термодинамические процессы назвали политропными, а линию этих процессов – политропой (политропный(греч.) – многообразный, многосторонний; поли – много, тропос - путь). Таким образом, политропы – это кривые, описывающие термодинамические процессы в идеальных газах, в которых происходит изменение всех термодинамических параметров. Соответственно, теплоёмкость политропного процесса получила название политропной теплоёмкости.
При использовании удельной политропной теплоёмкости СП,уд удельное количество тепла в политропном процессе qп определяется как
. (7.6.1)
В (7.6.1) следует иметь ввиду, что в политропном процессе нет понятия истинная теплоёмкость, так как на температурном интервале от Т 1 до Т 2, политропная удельная теплоёмкость газообразного рабочего тела является по определению средней политропной удельной теплоёмкости.
Подставляя (7.6.1) в уравнения 1-го закона термодинамики, получаем:
(7.6.2)
или
(7.6.3)
Разделив почленно нижнее уравнение системы на верхнее, получим:
. (7.6.4)
Левая часть (7.6.4) получила название показателя политропы и обозначение латинской буквой «n». Тогда:
. (7.6.5)
Интегрируя (7.6.5), учитывая при этом, что «n» является постоянной величиной, получим:
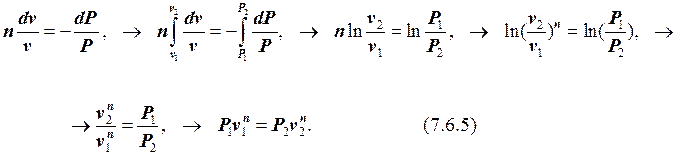
Следовательно, можем записать:
Pvn = const. (7.6.6)
Полученное уравнение является уравнением политропного процесса. В каждом конкретном процессе величина «n » постоянна, но для различных процессов показатель политропы может принимать любое численное значение от 
до 
Вид уравнения (7.6.6) полностью совпадает с видом уравнения адиабатного процесса (7.5.4), они различаются только показателями степени при v. Поэтому по аналогии с адиабатным процессом можно получить и другие виды уравнения (7.6.6):
, (7.6.7)
(7.6.8)
Определим теперь величину 
:
Таким образом: 
Уравнение (7.6.9) позволяет определить теплоёмкость политропного процесса для каждого значения «n». В отличие от теплоёмкостей 
и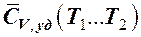 
теплоёмкость газообразного РТ в политропных процессах при > n > 1 может быть даже отрицательной. Это означает, что, несмотря на подвод тепла к рабочему телу, его температура падает и, наоборот, при отводе тепла она растёт. Это необычное на первый взгляд поведение Т объясняется тем, что политропные процессы с
> n > 1 и, следовательно, с < 0, реализуются при сильном расширении с подводом небольшого количества тепла. В этом случае lд > qп, где lд – удельная работа деформирования (положительная, так как имеет место процесс расширения) рабочего тела в политропном процессе, Дж; qп – удельная теплота, поступающая в рабочее тело и, следовательно, считающаяся положительной, Дж, поэтому изменение внутренней энергии оказывается отрицательным, то есть 
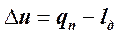< 0.
В процессе сжатия рабочего тела, когда от него отводится тепла меньше, чем подводится работы (в этом случае и тепло и работа являются отрицательными величинами), то есть когда ½ lд ½> ½ qп ½, изменение внутренней энергии оказывается положительным, то есть 
> 0, что приводит к росту температуры рабочего тела.
Поскольку уравнение политропы отличается от уравнения адиабаты только показателем степени при v, то все соотношения между основными параметрами политропного процесса описываются теми же уравнениями, что и у адиабатного процесса:
. (7.6.10)
Соответственно, работы располагаемая и деформирования в политропном процессе будут:
lрас = n | lд |. (7.6.11)
Учитывая (4.5.3) величину lд можно найти и несколько иным способом. Учитывая, что согласно(4.5.4):
получим:
.
Если при адиабатном процессе располагаемая работа всегда больше (по модулю) работы деформирования, то при политропном процессе в зависимости от величины «n» располагаемая работа может быть как больше работы деформирования, так и меньше её.
Изменение внутренней энергии газообразного рабочего тела и количество тепла в политропном процессе определяются по формулам:
Изменение энтальпии рабочего тела в этом процессе определяется по формуле (7.5.19):
,
которую, при необходимости, учитывая (7.6.9) и то, что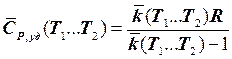 
можно легко преобразовать к следующему виду:
Изменение энтропии в политропном процессе в принципе можно определять по формулам (6.4.3), (6.4.6) и (6.4.8). Можно также определить 
и несколько другим способом. Для этого запишем (6.2.2) применительно к политропному процессу:
.(7.6.16)
После интегрирования получаем:
. (7.6.17)
Учитывая (7.6.10), получаем:
, (7.6.18)
. (7.6.19)
Значение показателя политропы «n» определяют на основании экспериментальных данных, полученных при исследовании реальных ТП. В этих исследованиях зачастую определяются только два из трёх основных термодинамических параметров, например Р и v. Полученная экспериментальная кривая Р(v), представленная на Рv –диаграмме, обычно состоит из ряда политроп с разными значениями «n». Поэтому сначала определяют среднее значение «n» для всей кривой в целом. Для этого используются уравнения политропы в начальной и конечной точках процесса:
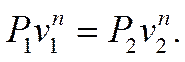(7.6.20)
Логарифмируя это уравнение, получим:
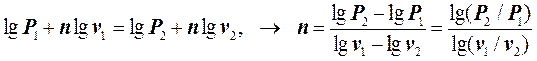. (7.6.21)
Если полученное таким образом уравнение политропы не обеспечивает необходимую точность расчётов, то тогда кривую процесса разбивают на ряд участков и для каждого из этих участков определяют свой показатель политропы.
Учитывая (7.6.9), можно из (7.6.21) получить уравнения для расчётов «n» с помощью параметров Р, Т и v, Т:
аналогично получим:
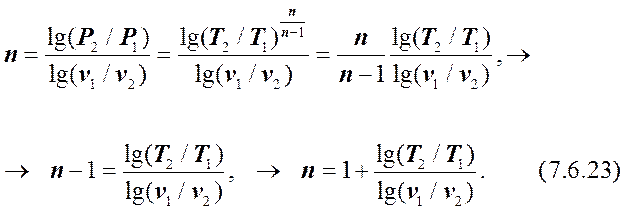
Таким образом, для определения показателя политропы достаточно знать начальные и конечные параметры процесса.
Все рассмотренные выше процессы: изохорный, изобарный, изотермический, адиабатный – являются частными случаями политропного процесса.
Действительно, при n = 0 уравнение политропы получает вид:
Рv 0 = Р ×1 = const или Р = const (изобарный процесс). При n = 1 уравнение политропы превращается в уравнение изотермического процесса: Рv = const. При n = k уравнение политропы превращается в уравнение адиабаты: Рvk = const. При n = ± 
(при очень больших абсолютных значениях «n») уравнение политропы преобразуется в уравнение изохоры. Извлекая из уравнения политропы корень n -ой степени, получаем:
При n ® ± величина (1/ n) ® 0, а следовательно 
Тогда при n = ± получаем v = const.
Учитывая (7.6.8), определим долю тепла, расходуемого на изменение внутренней энергии РТ в политропном процессе:
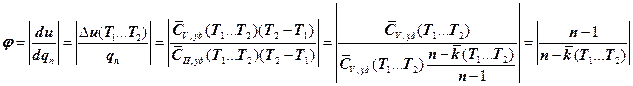. (7.6.24)
Соответственно доля тепла расходуемого на работу деформирования будет:
(7.6.25)
