5. Для проведения теста Манна – Уитни снова разделим наблюдения на две подвыборки -  и
и 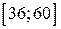 . Отсортируем теперь все элементы по возрастанию, запомнив, к какой из подвыборок они относятся (таблица 2.1.):
. Отсортируем теперь все элементы по возрастанию, запомнив, к какой из подвыборок они относятся (таблица 2.1.):
Таблица 2.1.
| Отсортированные значения ряда | Принадлежность к выборке | Ранги критерия Манна - Уитни | Ранги критерия Сиджела - Тьюки | Отсортированные значения ряда | Принадлежность к выборке | Ранги критерия Манна - Уитни | Ранги критерия Сиджела - Тьюки | Отсортированные значения ряда | Принадлежность к выборке | Ранги критерия Манна - Уитни | Ранги критерия Сиджела - Тьюки |
Сумма рангов для первой подвыборке равна: 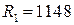 .
.
Тогда стандартизованная переменная, рассчитанная по формуле:
 ,
,
где  .
.
Будет равна: 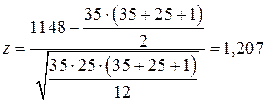 .
.
Статистика Манна – Уитни имеет стандартное нормальное распределение. Значение квантиля стандартного нормального распределения при уровне значимости  равно
равно 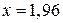 . Так как
. Так как  , то гипотеза о постоянстве математического ожидания принимается.
, то гипотеза о постоянстве математического ожидания принимается.
6. Для критерия Сиджела – Тьюки выборку также разбиваем на 2 части: в первой – 35 наблюдений, во второй – 25. Сортируем элементы по возрастанию и присваиваем ранги в следующем порядке: наименьшему – ранг 1, наибольшему – ранг 2, следующему за наименьшим - ранг 3, следующему наибольшему – ранг 4 и т.д. (см. табл. 2.1.)
Просуммировав ранги первой подвыборки, получим 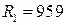 . Рассчитаем:
. Рассчитаем:
 .
.
Статистика Сиджела - Тьюки имеет стандартное нормальное распределение. Значение квантиля стандартного нормального распределения при уровне значимости  равно
равно 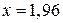 . Так как
. Так как  , то гипотеза о постоянстве дисперсии не отклоняется.
, то гипотеза о постоянстве дисперсии не отклоняется.
7. При тестировании по критерию Вальда – Вольфовитца сначала производится сортировка всех элементов выборки по их возрастанию и определяется медиана:
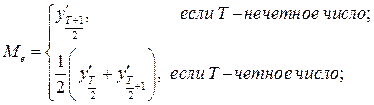 ,
,
где  - значения упорядоченной выборки. В нашем случае:
- значения упорядоченной выборки. В нашем случае:
 .
.
Возвращаемся к исходному ряду и рассчитываем разность между каждым элементом и медианой. Ставим напротив элемента знак «+», если элемент больше медианы и «‑», если элемент меньше медианы.
Получим следующее чередование «+» и «‑» (таблица 2.2.)
Таблица 2.2.
| - | + | - | + | - | + | + | - | + | - | + | - | + | - | + | - | + | + | - | + |
| - | + | - | + | - | + | - | - | - | + | - | + | + | + | - | + | - | + | - | + |
| - | + | - | + | - | + | - | + | - | + | - | + | + | - | + | - | - | - | + | - |
Общее число серий 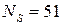 , количество элементов с положительным знаком
, количество элементов с положительным знаком  и количество элементов с отрицательным знаком
и количество элементов с отрицательным знаком  .
.
Среднее значение числа серий будет равно:

а его дисперсия:

Нормированная переменная 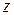 , определяемая как
, определяемая как

распределена по стандартизованному нормальному закону N (0,1). Так как  , то нельзя отклонить гипотезу о постоянстве математического ожидания.
, то нельзя отклонить гипотезу о постоянстве математического ожидания.






