Примечание: критическое значение - критерия Стьюдента находится либо с помощью статистических таблиц, либо с помощью встроенной функции в Excel: СТЬЮДРАСПОБР.
2. Проверка гипотезы о постоянстве дисперсии временного ряда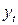 
в случае разбиения исходного интервала на две части осуществляется с использованием двухстороннего критерия Фишера. Расчетное значение критерия Фишера определяется:
(
).
Для нашего примера расчетное значение критерия Фишера равно: 
. Сравнивая его с табличным значением критерия Фишера с 34 и 24 степенями свободы: 
, можно сделать вывод, о том, что гипотеза о постоянстве дисперсии отвергается, так как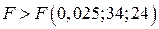 
.
3. При разбиение ряда на несколько частей для проверки гипотезы о постоянстве дисперсий может быть использован критерий Кокрена, основанный на распределении Фишера. Он применяется в предположении, что объемы этих частей равны между собой. Расчетное значение этого критерия определяется: 
, где 
.
Табличное значение критерия Кокрена, соответствующее заданной доверительной вероятности и числам степеней свободы (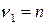
, 
), определяется на основании табличного значения 
–критерия: 
, где 
- табличное значение критерия Фишера, выбранное для уровня доверительной вероятности 
и числа степеней свободы 
и 
. Если оказывается справедливым соотношение 
, то гипотеза о постоянстве дисперсии временного ряда принимается.
В нашем примере разобьем ряд на 5 равных частей. Обозначим через 
число наблюдений в подвыборке. В нашем случае 
. Для каждой из подвыборок рассчитаем дисперсию по формуле: 
. В результате получаем:
;
;
;
;
.
Статистика критерия Кокрена определяется следующим образом:
Рассчитаем критическое значение:
.
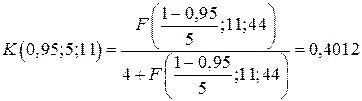Поскольку расчетное значение меньше критического значения, нельзя отвергнуть гипотезу о постоянстве дисперсии.
Примечание: в Excel табличное значение рассчитывается с помощью встроенной функции FРАСПОБР.
4. Данный критерий основан на использовании распределения Пирсона - 
. Согласно этому критерию случайная величина 
, рассчитанная как: 
, распределенная примерно по закону с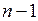 
степенями свободы, где 
- оценка дисперсии на 
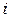–ом интервале; 
- средняя дисперсия на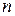 
интервалах; 
- число степеней свободы.
Величина 
рассчитывается по формуле: 
.
Когда 
получаем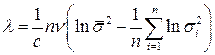 
, где 
.
Если оказывается, что 
, то гипотеза о постоянстве дисперсии временного ряда принимается.
В нашем примере разобьем ряд на 3 части: первая – с 1 по 20, вторая – с 21 по 40, третья – 41 по 60. Рассчитаем среднее значение для подвыборок:
; 
; 
.
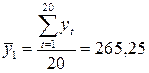Определим дисперсии:
;
;
.
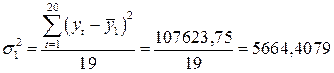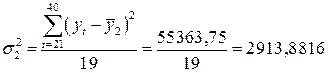Общая дисперсия для всей выборки:
.
Т.к. 
получаем, при 
.
Статистика Бартлетта имеет распределение 
- Пирсона с 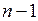степенью свободы. И так как 
, поэтому нельзя отклонить гипотезу о постоянстве дисперсии.
