Лекция 2
Главной целью расчета нефтехимических аппаратов является вычисление их основных размеров. При этом предполагается, что процесс изучен во всем объеме и найдено уравнение связи между коэффициентом скорости процесса и величинами, определяющими его течение.
Процессы химической технологии очень сложны; для математического их описания удается составить только сложные дифференциальные уравнения, которые лишь приближенно отражают их протекание. Поэтому возникает необходимость опытного изучения процессов.
Изучение процессов опытным путем возможно только при наличии теории постановки опытов и обработки их результатов. Такой теорией является теория подобия.
Она отвечает па вопрос, как нужно организовать опыт и обработать полученные данные, чтобы их можно было обоснованно распространить на процессы, протекающие в условиях, отличных от условий опыта.
Первые понятия о подобии (механическом) были даны Ньютоном в 1686г. Основы теории подобия в современном понимании были заложены известным русским ученым В. Л. Кирпичевым еще с 1874 г. Его идеи позднее были развиты в трудах В. Нуссельта, М.В. Кирпичева, Г. К Дьяконова, И. Бэкингема и др. Ихработы дали возможность использовать представления о подобии в различных отраслях науки и техники.
Представление о подобии процессов позволяет:
1) установить условия экспериментальных работ, при которых число требующихся опытов будет минимальным;
2) определить наименьшее число величин, которые нужно измерять при проведении опытов, и правильно обработать результаты опытов;
3) установить области, на которые можно распространить данные, полученные в результате проведенного опыта.
Выводы теории подобия строятся на основании особых форм исследования дифференциальных уравнений, описывающих течение изучаемого процесса.
При составлении дифференциального уравнения процесс рассматривают не во всем исследуемом объеме и не за весь исследуемый промежуток времени, а в произвольно выделенном элементарном объеме в течение произвольно выбранного малого интервала времени. Выделенный элементарный объем настолько мал по сравнению со всем исследуемым объемом, что его линейные размеры могут быть приняты за дифференциалы длины. Применительно к изучаемому в элементарном объеме процессу дается математическая формулировка соответствующего общего закона физики.
Математические выражения, формулирующее таким способом общие законы физики, представляет собой дифференциальное уравнение, описывающее течение изучаемого процесса в любом элементарном объеме в любой момент времени.
При составлении дифференциального уравнения отвлекаются от частных особенностей процесса, поэтому оно описывает целый класс процессов, в пределах которого действуют примененные физические законы. Дифференциальное уравнение по существу не может описывать какой-нибудь единичный процесс, оно описывает бесчисленное множество однородных процессов.
Чтобы описать единичный процесс, нужно дополнить дифференциальное уравнение данными, характеризующими его, но не присущие всему рассматриваемому классу процессов. Эти дополнительные данные называют условиями однозначности.
Условия однозначности включают особенности процесса, к ним относятся:
1) геометрические размеры и форма объема, в котором протекает процесс;
2) физические свойства среды, существенные для рассматриваемого процесса;
3) граничные условия, характеризующие взаимодействие среды с телами, ограничивающими объем, в котором протекает процесс;
4) начальное состояние системы, т.е. ее состояние в момент, когда начинается изучение процесса.
Условия однозначности, заданные в виде конкретных численных значений, в соединении с дифференциальным уравнением выделяют из всего класса один конкретный процесс. В этом случае решение дифференциального уравнения, если его удается получить, справедливо только для заданных численных условий однозначности.
При проведении опыта изучаемый процесс протекает в аппарате, имеющем конкретные размеры и форму, в среде, обладающей определенными физическими свойствами, при определенных граничных и начальных условиях. Полученные в опытах данные соответствуют конкретным условиям однозначности и дают практическое решение вопроса для единичного процесса точно так же, как численное решение дифференциального уравнения при конкретных значениях величин, определяющих условия однозначности.
Переносить данные единичного опыта на целый класс процессов практически неверно, так как в пределах одного класса ввиду резкого отличия условии однозначности имеются совершенно различные процессы.
Теория подобия позволяет распространить данные единичного опыта па определенную группу подобных процессов в пределах рассматриваемого класса путем особого способа задания условий однозначности. Это дает возможность переносить опытные данные с модели на подобный промышленный объект.
Для выделения из класса группы подобных процессов условия однозначности задаются не в виде определенных численных значений отдельных параметров, а в форме произведения соответствующих параметров на постоянные числовые множители.
Подобие условий однозначности включает геометрическое подобие систем, временное подобие, подобие физических величин, характеризующих процесс, подобие граничных и начальных условий.
Геометрическое подобие аппаратов (систем), в которых протекает изучаемый процесс, соблюдается, если отношение всех сходственных размеров двух сравниваемых аппаратов является величиной постоянной (при этом соответствующие углы должны быть равны), т.е. (рис. 1):
l1’’/l1’=l2’’/l2’=l3’’/l3’=…Kl или l1’’=Kl/l1’; l2’’=Kl/l2’; l3’’=Kl/l3’ (1)
где l1’, l2’, l3’ — размеры, характеризующие первый аппарат; l1’’, l2’’, l3’’ — размеры, характеризующие второй аппарат, подобный первому; Kl — множитель линейного (геометрического) преобразования, сохраняющий постоянное значение для двух подобных аппаратов (при переходе к третьему аппарату, подобному первому, множитель преобразования Kl получает другое значение)

Рис. 1. Геометрически подобные аппараты
Временное подобие соблюдается, если отношение между сходственными интервалами времени процесса сохраняет постоянное значение. Сходственные интервалы – это интервалы, в течение которых завершаются аналогичные стадии рассматриваемых процессов. Временное подобие характеризуется соотношением
τ1’’/τ1’=τ2’’/τ2’=τ3’’/τ3’=…Kτ или τ1’’=Kτ/τ1’; τ2’’=Kτ/τ2’; τ3’’=Kτ/lτ’ (2)
где τ1', τ2', τ3' — интервалы времени в первом процессе; τ1'', τ2'', τ3''— интервалы времени во втором процессе, подобном первому; Kτ - множитель временного преобразования, сохраняющий постоянное значение для двух подобных процессов.
Временное подобие может быть пояснено на следующем примере. В двух аппаратах протекают за различные интервалы времени аналогичные стадии процесса: загрузка в аппарат перерабатываемого материала за время соответственно τ1’ и τ1’’, нагревание его (τ2’ и τ2’’) перемешивание (τ3’ и τ3’’), охлаждение (τ4’ и τ4’’) и выгрузка из аппарата готового продукта (τ5’ и τ5’’). Общая продолжительность процесса в первом аппарате
τ’ = 2 ч, во втором τ’’ = 1 ч. Тогда Kτ = τ’’:τ’ = 1: 2 = 0,5. Каждая из аналогичных стадий процесса в первом и втором аппаратах совершается за различные интервалы времени, однако соотношение между интервалами времени протекания двух сходственных стадий сохраняется постоянным:
Kτ =τ’’/τ’=τ1’’/τ1’=τ2’’/τ2’=…=τ5’’/τ5’=0,5 (3)
Временное подобие процессов называют гомохронностыо (однородностью во времени).
Одновременность протекания процессов, являющаяся частным случаем гомохронности (при Kτ=l), и называется синхронностью; в этом случае сходственные моменты времени совпадают.
Подобие физических величин, характеризующих процесс, соблюдается, если отношение значений этих величин для подобных процессов в сходственные моменты времени является величиной постоянной, т.е.
ρ1’’/ρ1’=ρ2’’/ρ2’=ρ3’’/ρ3’=…Kρ или ρl1’’=Kρ/ρ1’; ρ2’’=Kρ/ρ2’; ρ3’’=Kρ/ρ3’ (4)
где ρ1' ρ2', ρ3'— значения физических величин в первом процессе; ρ1", ρ2", ρ3" - их значения во втором процессе, подобном первому; Кρ - множитель преобразования значений физических величин.
Если значение физических величин не постоянно во всем объеме, охваченном процессом, то для подобных процессов должно соблюдаться подобие полей физических величин.
Полем физической величины называют совокупность мгновенных значений физической величины во всем объеме, охваченном процессом. Подобие полей физических величин соблюдается, если отношение значений этих величин для подобных процессов в сходственных точках объема в сходственные моменты времени является величиной постоянной.
Если рассматриваются векторные физические величины, то для подобных процессов направление их должно совпадать.
Следует отметить, что множители преобразования Kl, Kτ, Kρ численно отличаются друг от друга, т.е. для каждой переменной, характеризующей процесс, существует свой множитель преобразования.
Подобие граничных условий определяется тем, что все значения величин, характеризующих эти условия на границах системы, для сходственных точек в сходственные моменты времени находятся в постоянных соотношениях.
Подобие начальных условий означает, что в момент, когда начинается изучение процесса (начальный момент), соблюдается подобие полей всех физических величин во всем объеме, охваченном изучаемым процессом.
Условия однозначности являются индивидуальными признаками различных процессов одного и того же класса. Если все индивидуальные признаки подобны, то процессы также подобны, т.е. представляют собой один процесс, протекающий в различных масштабах.
Понятие подобия процессов значительно шире, чем понятие, подобия условий однозначности. Подобие процессов распространяется на весь объем и на весь период их протекания. Подобие условий однозначности распространяется на весь объем только в начальный момент, а в последующие моменты условия однозначности определяют подобие только на границе.
Процессы подобны, если они описываются одним и тем же дифференциальным уравнением (или системой уравнений) при подобных условиях однозначности.
Следовательно, для соблюдения подобия нужно найти и выдержать условия, при которых умножение переменных на постоянные множители не меняло бы уравнения.
Это возможно, если комплекс из произведений постоянных величин (множителей преобразования), входящий в уравнение, будет равен единице.
В каждом из подобных процессов комплексы изменяются в пространстве и во времени. Но изменения эти происходят так, что для любых сходственных точек объема в сходственные моменты времени комплексы во всех подобных процессах принимают одно и то же значение.
Безразмерные комплексы играют большую роль в теории подобия и получили название чисел подобия.
Числа подобия обычно обозначают двумя первыми буквами фамилий ученых, известных своими работами в соответствующей области наук. Полученное число называется числом Ньютона, оно определяет механическое подобие:
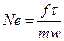
В теории подобия числа подобия получают из дифференциальных уравнений любой степени сложности по следующей схеме:
1) запись дифференциального уравнения, описывающего исследуемый процесс;
2) получение из дифференциального уравнения безразмерного комплекса делением обеих частей уравнения на правую пли левую часть; при наличии в дифференциальном уравнении нескольких слагаемых безразмерные комплексы получают делением всех слагаемых на одно из них (следует иметь в виду, что в правильно составленном уравнении все слагаемые имеют одну и ту же размерность);
3) вычеркивание символов дифференцирования, включая символы порядка дифференцирования;
4) символы, показывающие, степени дифференциалов, сохраняются; символы суммирования аналогичных членов дифференциального уравнения и индексов, характеризующих направление, вычеркиваются.
Указанная схема получения чисел подобия из диффх уравнений применяется во всех разделах курса.
Кроме чисел подобия, получаемых из дифференциальных уравнений, применяют числа подобия, характеризующие условия задачи исследования. Например, при исследовании движения жидкости по змеевику задают диаметр трубы и радиус змеевика. Очевидно, что процессы, происходящие при движении жидкости, в этом случае будут зависеть от соотношения характеризующего данную группу явлений: d/R=idem
Обозначение idem с ледует понимать как «одно и то же».
Числа подобия, представляющие собой отношение двух одноименных величин и получающиеся непосредственно из условий задачи исследования, называют параметрическими числами подобия.
Физические величины, характеризующие процесс, могут иметь различное значение для разных точек объема, охваченного процессом. В этом случае обычно пользуются усредненными значениями физической величины. Числа подобия, составленные из усредненных значений физических величин, называют усредненными числами подобия.
Если в выражение числа подобия входит линейный размер, то выбирают тот размер, который наиболее полно характеризует систему, охваченную процессом (например, диаметр - при рассмотрении процесса движения жидкости по трубе).
Линейный размер, включаемый в число подобия и являющийся наиболее характерным для рассматриваемой системы, называют определяющим, или характерным линейным размером.
В подобных процессах все числа подобия, характеризующие процессы, изменяются так, что для любой сходственной точки объема в сходственные моменты времени они принимают одно и то же значение.
Для обеспечения подобия необходимо равенство определяющих чисел подобия, составленных только из физических величин, входящих в условия однозначности. Определяющие числа подобия называют также определяющими критериями подобия. Равенство определяющих критериев подобия является условием подобия процессов.
Числа подобия, в состав которых входит хотя бы одна физическая величина, не входящая в условия однозначности, называют определяемыми числами подобия.
Следует отметить, что в различных задачах условия однозначности могут формулироваться по-разному. Поэтому при изменении формулировки условии однозначности определяющими могут стать другие числа подобия. Одно и то же число подобия в различных задачах может быть и определяющим, и неопределяющим. Только параметрические критерии подобия являются всегда определяющими.
Равенство определяющих чисел подобия свидетельствует о подобии процессов, а при подобии процессов равны все числа подобия. Отсюда следует, что неопределяющие числа подобия являются функцией определяющих чисел подобия. Эта функциональная зависимость распространяется на всю группу подобных процессов и называется уравнением подобия.
Представление зависимости между физическими величинами, характеризующими процесс, в виде уравнения подобия, справедливого для целой группы подобных процессов и позволяет распространять на нее данные единичного опыта.
В опытах нужно измерять все величины, входящие в числа подобия изучаемого процесса. Результаты опытов нужно представлять в виде функциональной зависимости между числами подобия. Обычно эта зависимость дается в виде графика или в виде степенных функций.
Пусть, например, при исследовании какого-либо процесса было выведено дифференциальное уравнение, описывающее его. Из него и условий однозначности были найдены числа подобия, характеризующие процесс; неопределяющее Kн и определяющие Ко1 и Кo2. Кроме того, из анализа условия задачи исследования было получено параметрическое число подобия Коз. Связь между физическими величинами, характеризующими процесс, может быть представлена уравнением подобия в виде степенных функций:
Кн = АКп01Кт02Кt03, (1)
где A, п, т и t —постоянные, определяемые опытным путем.
Первую серию опытов проводят в условиях, при которых какие-нибудь два определяющих числа подобия в правой части уравнения подобия (1) сохраняют постоянное значение, например числа подобия Кo2 и Коз. Тогда для первой серии опытов имеем
АКт02Кt03 = const = В
и уравнение подобия (1) принимает вид (2), а после логарифмирования - вид (3):
Кн = ВКn01 (2) lg Кн = IgB + n lg Коз (3)
При проведении опытов находят ряд конкретных значений чисел подобия Ко1 и соответствующих им значений числа подобия Кн. По этим значениям на график в координатах lg Ко1—lg Кн наносят точки; по точкам наилучшим образом проводят прямую. Как следует из уравнения (3), тангенс угла наклона этой прямой к оси абсцисс равен показателю степени при числе подобия Ко1. Аналогично определяют опытным путем остальные постоянные уравнения подобия (1).
Применительно к различным процессам в дальнейшем будут рассмотрены соответствующие числа подобия и уравнения подобия.






