ЗАДАНИЕ
Механизм гайковырубного автомата:

Рисунок 1 - Рычажный механизм
Таблица 1 - Исходные данные для проектирования
| Параметры | Обозначение | Размерность | Числовое значение |
| Размеры звеньев рычажного механизма | O1A | м | 0.09 |
| AB | м | 0.43 | |
| O2B | м | 0.25 | |
| BD | м | 0.25 | |
| a | м | 0.24 | |
| b | м | 0.45 | |
| Угол поворота крывошипа | 
| ||
| Частота вращения крывошипа | n | об/мин | |
| Массы звеньев рычажного механизма | m1 | кг | |
| m3 | кг | ||
| m4 | кг | ||
| m5 | кг | ||
| Моменты инерции звеньев | J1 | 
| 1.2 |
| J2 | 
| 0.2 | |
| J3 | 
| 0.09 | |
| J4 | 
| 0.09 | |
| Сила сопротивления | Fp | кН |
Оглавление
ЗАДАНИЕ. 1
ВВЕДЕНИЕ. 3
1. СТРУКТУРНЫЙ АНАЛИЗ РЫЧАЖНОГО МЕХАНИЗМА.. 4
1 ИСХОДНЫЕ ДАННЫЕ. 8
2 ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ ТОЧЕК И ЗВЕНЬЕВ МЕХАНИЗМА МЕТОДОМ ПЛАНА.. 9
3 Определение ускорений точек и звеньев механизма методом плана.. 11
4 Силовой анализ механизма.. 14
4.1 Силовой анализ механизма по группам Ассура. 14
4.2 Первая группа 5-4. 15
4.2 Метод жесткого рычага Жуковского. 18
Список литературы.. 20
ВВЕДЕНИЕ
Начальная стадия проектирования машин и механизмов требует от инженера качественного выполнения анализа и синтеза проектируемой машины, а также разработки её кинематической схемы, которая обеспечивает с достаточным приближением воспроизведение требуемого закона движения. Это необходимо для того, чтобы конструктору было легче понять как устроен механизм, как он работает, по каким законам происходит его движение.
Цель курсового проекта - развить у студента навыки самостоятельного решения комплексных инженерных задач, приобретение навыков оформления конструкторской документации в соответствии с требованиями ЕСКД.
Объектом исследования является рычажный механизма гайковырубного автомата. Рычажный механизм служит для преобразования возвратно-поступательного перемещения ползуна из вращательного движения кривошипа.
Проект по разработке (анализу и синтезу) механизма гайковырубного автомата выполнен в соответствии с исходным заданием и методическими указаниями на курсовой проект [1].
СТРУКТУРНЫЙ АНАЛИЗ РЫЧАЖНОГО МЕХАНИЗМА

Рис. 1 Кинематическая схема гайковырубного автомата
Рассматриваемый в данном проекте рычажный механизм состоит из стойки 0, кривошипа 1, шатуна 2, коромысла 3, шатуна 4 и ползуна 5 (рис. 1).
Перечислим все одноподвижные пары:
кривошип 1 образует вращательную пару со стойкой и шатуном 2;
кулиса 3 входит во вращательную пару с шатуном 2 и стойкой и в поступательную пару с шатуном 4;
ползун 5 входит во вращательную пару с шатуном 4 и в поступательную пару с звеном 3.
Таблица 2 - Кинематические пары
| № кинематической пары | Тип кинематической пары | Класс кинематической пары |
| I (стойка 0 - кривошип 1) | вращательная | |
| II (кривошип 1 -шатун 2) | вращательная | |
| III (шатун 2 - кулиса 3) | поступательная | |
| IV (кулиса 3 - стойка 0) | вращательная | |
| V (кулиса 3 - шатун 4) | вращательная | |
| VI (шатун 4 - ползун 5) | вращательная | |
| VII (ползун 5 - стойка 0) | поступательная |
Таким образом, число подвижных звеньев n = 5; число одноподвижных пар p1 = 7.
Кинематическая цепь механизма плоская, сложная, замкнутая. Число степеней подвижности определяем по формуле Чебышева [2]:
W = 3n - 2p1 - p2 = 3×5 - 2×7 - 0 = 1,(1)
Исследуемый механизм имеет одну обобщенную координату: угол поворота начального звена 
Для установления класса механизма, определим наивысший класс группы Аcсура, входящей в его состав. Отделение структурных групп начинаем с группы, наиболее удаленной от начального звена. В заданном механизме наиболее отдалена от начального звена группа второго класса второго вида со звеньями 4 и 5 (ВВП) (рисунок 2, a).



Рисунок 2 - Структурные группы механизма:
а - группа второго класса второго вида (ВВП); б - группа второго класса второго вида (ВВВ); в - механизм первого класса
Затем отделяем группу второго класса второго вида со звеньями 2 и 3 (ВВВ) (рисунок 2, б).
В результате остается механизм первого класса, в состав которого входит начальное звено 1 и стойка 0 (рисунок 3, в).
Механизм образован последовательным присоединением к начальному звену двух структурных групп второго класса. Поэтому по классификации Ассура-Артоболевского, его следует отнести ко второму классу.
Формула строения рассматриваемого механизма имеет вид:
I(1) ® II(2,3) ® II(4,5).
ИСХОДНЫЕ ДАННЫЕ

Гайковырубной автомат.
a = 240 мм. J1 = 1.2 кг·м2.
b = 450 мм. m2 = 11 кг. J2 = 0.2 кг·м2.
ОА = 90 мм. m3 = 15 кг. J3 = 0.09 кг·м2.
АВ = 430 мм. m4 = 25 кг. J4 = 0,09 кг·м2.
ВО2 = 250 мм. m5 = 60 кг.
ВD = 250 мм.
n = 100 об/мин.
Fp = 60 кН.
ОПРЕДЕЛЕНИЕ СКОРОСТЕЙ ТОЧЕК И ЗВЕНЬЕВ МЕХАНИЗМА МЕТОДОМ ПЛАНА
По исходным данным определим угловую скорость 1 звена:


Определим модуль скорости точки А начального звена 1:


Для дальнейших построений необходимо определить масштабный коэффициент скорости:
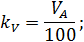

Основу построения плана скоростей составляет векторная формула определения скорости точки плоской фигуры.
Составим системе векторных уравнений для скорости точки В:

Графически решив систему уравнений, получим скорость точки В.
Аналогично составим векторное уравнение для точки D:
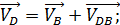
Проводим из конца вектора  прямую, перпендикулярную звену 4, а из полюса
прямую, перпендикулярную звену 4, а из полюса  – прямую, параллельную направляющим ползуна 5. Точка пересечения этих прямых и будет концом вектора
– прямую, параллельную направляющим ползуна 5. Точка пересечения этих прямых и будет концом вектора  .
.
По плану скоростей определим модули скоростей всех точек механизма:
Линейные скорости:

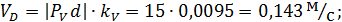


Угловые скорости:



Определение ускорений точек и звеньев механизма методом плана
Построение плана ускорений начинается с того что нужно определить ускорение точки А для 1 звена:
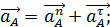
Где  и
и  , соответственно нормальная и касательная составляющая ускорения точки А. Так как 1 звено вращается с постоянной скоростью, то
, соответственно нормальная и касательная составляющая ускорения точки А. Так как 1 звено вращается с постоянной скоростью, то  =0;
=0;
Следовательно  , отсюда:
, отсюда:


Далеевыбираем масштабный коэффициент:


Далее определим значения нормальных составляющих ускорений точек механизма, а также длины их отрезков на плане ускорений:

Ускорению  соответствует отрезок
соответствует отрезок  на плане ускорений, его длина равна:
на плане ускорений, его длина равна:

Далее аналогично:




Запишем систему векторных уравнений для ускорения точки В:

Распишем ускорения  и
и  через их составляющие, получим:
через их составляющие, получим:

Аналогично составим векторное уравнение для точки D:

Проводим из конца вектора  прямую, перпендикулярную звену 4, а из полюса
прямую, перпендикулярную звену 4, а из полюса  – прямую, параллельную направляющим ползуна 5. Точка пересечения этих прямых и будет концом вектора
– прямую, параллельную направляющим ползуна 5. Точка пересечения этих прямых и будет концом вектора  .
.
По плану ускорений определим модули ускорений всех точек механизма:
Линейные ускорения:


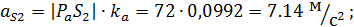

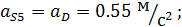
Касательные ускорения:



Угловые ускорения:



Силовой анализ механизма




