| Режим движения жидкости | |||
| Ламинарный | Турбулентный | ||
| Гидравлически гладкие трубы | Гидравлически шероховатые трубы | ||
| Область доквадратичного сопротивления | Область квадратичного сопротивления | ||
| Re < 2300 |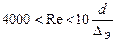 
| 
| 
|
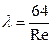λ = f (Re)
hl ~ V 1
| Формула Блазиуса
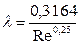λ = f (Re)
hl ~ V 1,75
| Формула Альтшуля
λ = f (Re, Δэ/d)
hl ~ V 1,75…2,00
| Формула Шифринсона
λ = f (Δэ/d)
hl ~ V 2
|
Методика определения области гидравлического сопротивления:
1) Определить расход воды по формуле:
, см3/с
2) Определить площадь живого сечения трубопровода по формуле:
3) Определить среднюю скорость движения воды в трубопроводе по формуле: 
, см/с
4) Определить число Рейнольдса по формуле: 
5) Вычислить относительную гладкость трубопровода 
.
6) Пользуясь данными табл. 1, определить область гидравлического сопротивления трубопровода.
Выполнение лабораторной работы.
Описание установки.
Потери напора по длине определяются в прямом горизонтальном трубопроводе 1 с внутренним диаметром d=5,1 см на участке длиной l = 500 см (рис. 1). По справочным данным эквивалентная шероховатость трубопровода Δэ = 0,02 см.
В начале участка установлен пьезометр 11, в конце участка установлен пьезометр 12. Вода в трубопровод подается из питающего бака 2. Для определения расхода воды, проходящей по трубопроводу, установлен расходомер 4. Регулирование расхода воды в трубопроводе производится с помощью кранов 3 и 5.
После трубопровода 1 вода поступает в промежуточный бак 6. Система питания установки – оборотная, поэтому из бака 6 в бак 2 вода перекачивается по трубе 8 с помощью насоса 7. Уровень воды в баке поддерживается постоянным с помощью переливной трубы 9.
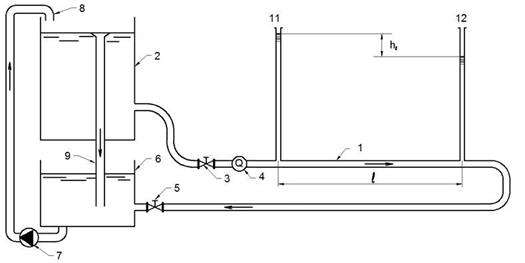
Рис. 1. Схема установки для изучения потерь напора по длине
В данной лабораторной работе определяется потеря напора по длине прямого горизонтального трубопровода (рис. 1) между сечениями 11 и 12 при напорном движении.
Напорное движение жидкости – движение жидкости, при котором жидкость со всех сторон ограничена жёсткими стенками, нет свободной поверхности. Напорное движение возникает в условиях, когда труба полностью заполнена жидкостью, и гидродинамическое давление во всех точках живого сечения выше атмосферного.
На участке 11—12 местные сопротивления отсутствуют. Поэтому hw = hl. Опытным путём потеря напора hl может быть определена как разность напоров в сечениях 11 и 12.
(6)
Выражение (6) представляет собой уравнение Бернулли
(7)
Для горизонтального трубопровода геометрические высоты во всех сечениях равны: z11=z12.
Согласно уравнению неразрывности потока, расход Q во всех сечениях трубопровода одинаков. Площадь живого сечения потока тоже не изменяется по длине потока. Следовательно, средняя скорость движения воды в трубопроводе 
и скоростная высота 
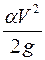во всех сечениях одинаковы. Это означает, что движение воды в трубопроводе равномерное. Таким образом,
(8)
и уравнение (7) преобразуется в выражение:
(9)
которое показывает, что в прямом напорном трубопроводе потеря напора по длине равна разности пьезометрических высот в начале и в конце рассматриваемого участка. Иными словами, при равномерном движении жидкости потери напора можно определять не только по напорной, но и по пьезометрической линии.
Таким образом, при проведении лабораторной работы опытное определение hl заключается в измерении разности
пьезометрических высот в пьезометрах 11 и 12 (рис. 1).
Эта формула применяется в лабораторной работе для опытного определения коэффициента гидравлического трения:
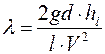(10)
Чтобы воспользоваться формулой (10), необходимо определить расход воды в трубопроводе так же, как это делается в других лабораторных работах
(11)
по расходу вычислить среднюю скорость движения воды
(12)
Таблица 2. Опытные данные
| № опыта | Объём жидкости | Время | Показания пьезометра | температура | Кинематический коэффициент вязкости | |
| W | t | 
| 
| t0C | υ | |
| см3 | сек | см | см | 0C | см2/сек | |
Диаметр трубы d = ______ см Площадь живого сечения трубы 
Длина трубы L = ________ см Экв. шероховатость Δэ = ______ см
Таблица 3. Расчётные данные
| № опыта | Потери напора | Расход жидкости | Средняя скорость | Число Рейнольдса | Область гидравлического сопротивления | Коэффициент гидравлического трения
| |
| 
| 
| 
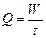
| по расчёту | из опыта | ||
| см | см3/сек | см/сек | – | - | - | - | |
Обработка опытных данных
1. Определение коэффициента гидравлического трения опытным путём:
1.1. Вычислить потерю напора по длине по формуле (9).
1.2. Вычислить расход воды по формуле (11).
1.3. Вычислить среднюю скорость движения воды в трубопроводе по формуле (12).
1.4. Вычислить коэффициент гидравлического трения опытным путём по формуле (10).
Все данные вычислений записать в табл. 3.
2. Определение коэффициента гидравлического трения по эмпирическим формулам (по расчёту):
2.1. Вычислить число Рейнольдса по формуле (3).
2.2. Определить режим движения в трубопроводе.
2.3. Вычислить относительную гладкость трубопровода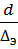 
.
2.4. Пользуясь данными табл. 1, определить область гидравлического сопротивления трубопровода.
2.5. Определить эмпирическую формулу, соответствующую найденной области гидравлического сопротивления (см. табл. 1).
2.6. Определить расчетное значение коэффициента гидравлического трения по соответствующей эмпирической формуле.
Все данные вычислений записать в табл. 3.
3. Сравнить коэффициент гидравлического трения λрасч., полученный по эмпирическим формулам с коэффициентом гидравлического трения λопыт., полученным опытным путём.
ВЫВОДЫ:
Лабораторная работа
