Основные теоретические сведения.

ЛАБОРАТОРНАЯ РАБОТА

«ПОТЕРИ НАПОРА ПО ДЛИНЕ»

 

 

Выполнил:
Студент группы
	курса		(ФИО студента)
Факультет:
Проверил:
	(ФИО преподавателя)

 

 

Санкт-Петербург, 2017

Лабораторная работа

ОПРЕДЕЛЕНИЕ ПОТЕРЬ НАПОРА ПО ДЛИНЕ ТРУБОПРОВОДА

 

Цели работы:

1) Определение потерь напора по длине трубопровода опытным путём.

2) Определение коэффициента гидравлического трения опытным путём.

3) Определение области гидравлического сопротивления.

4) Определение коэффициента гидравлического трения по эмпирическим формулам для соответствующей области гидравлического сопротивления.

 

Основные теоретические сведения.

Поток жидкости в трубопроводе затрачивает энергию на преодоление сил трения, которые возникают как в самой жидкости, так и между жидкостью и стенками трубопровода. Силы трения, преодолеваемые потоком, называются гидравлическими сопротивлениями. Поскольку удельная энергия жидкости, отнесенная к единице веса, именуется в гидравлике напором, затраты энергии на преодоление сил трения получили название потерь напора.

Различают два вида гидравлических сопротивлений и обусловленных ими потерь напора:

1) потери по длине потока h_l

2) местные потери напора h_м

 

Потери напора по длине в случае равномерного движения представляют собой затраты энергии на преодоление гидравлических сопротивлений, равномерно распределенных по длине потока.

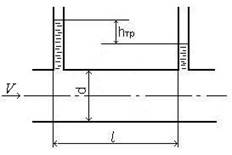
Местные потери напора в трубопроводе представляют собой затраты энергии на преодоление гидравлических сопротивлений, которые обусловлены локальными сопротивлениями, сосредоточенными на небольшом участке потока, например, на резком повороте, при резком расширении или резком сужении трубопровода и т. п.

Полная потеря напора в трубопроводе определяется суммированием потерь напора по длине трубопровода на отдельных участках и местных сопротивлений:

(1)

Где

h_l - потери по длине потока, м

h_м - местные потери напора, м

 

Гидравлические сопротивления по длине в напорных трубопроводах характеризуются безразмерным коэффициентом гидравлического трения λ, который входит в формулу Вейсбаха-Дарси для вычисления потерь напора по длине:

(2)

где

λ - коэффициентом гидравлического трения, безразмерный

l – длина рассматриваемого участка трубопровода, м

d – внутренний диаметр трубы, м

V – средняя скорость движения потока воды на участке, м/с

g – ускорение свободного падения, g=9,81 м/с²

Коэффициент гидравлического трения λ можно найти двумя способами:

1) Опытным путём из формулы Вейсбаха-Дарси

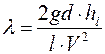
2) В инженерной практике коэффициент гидравлического трения чаще всего вычисляют по эмпирическим формулам.

Потери напора по длине трубопровода зависят от режима движения жидкости - для различных режимов используются разные формулы.

Режим движения потока жидкости определяют по числу Рейнольдса (см. лабораторную работу «Режимы движения жидкости»).

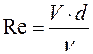(3)

где

d – внутренний диаметр трубы, см

V – средняя скорость движения потока воды на участке, см/с

– кинематический коэффициент вязкости, см²/с

 

При Re<2300 режим движения жидкости - ламинарный и коэффициент гидравлического трения λ вычисляют по формуле:

, (4)

которая выведена теоретическим путем.

При ламинарном режиме λ = f (Re) - коэффициент гидравлического трения λ зависит только от числа Рейнольдса, т. е. определяется скоростью движения жидкости, внутренним диаметром трубопровода и вязкостью жидкости. Принципиально важно то, что λ не зависит от шероховатости стенок трубы. Потери напора по длине прямо пропорциональны средней скорости движения жидкости. Установлено, что при ламинарном режиме движения потери напора минимально возможные.

В случае турбулентного режима не удается обойтись одной формулой для вычисления λ. Приходится различать гидравлически гладкие и шероховатые трубы. Различие между ними состоит в следующем. Силы молекулярного притяжения материала стенок трубы лишают возможности перемешивания частицы жидкости, которые находятся в непосредственной близости от стенок. Этот слой называют пограничным вязким (ламинарным) слоем. На самом деле считать движение в этом слое ламинарным не следует, поскольку в этом слое наблюдаются значительные продольные пульсации скорости. Однако практически отсутствуют пульсации поперек потока. Толщина пограничного слоя δ составляет сотые или тысячные доли внутреннего диаметра трубы.

Для вычисления толщины ламинарного пограничного слоя δ, мм,
получена полуэмпирическая формула:

(5)

где

d – внутренний диаметр трубы, мм

λ - коэффициентом гидравлического трения, безразмерный

Re – число Рейнольдса, безразмерный

Как видно из формулы (5), с увеличением скорости движения потока жидкости, а, следовательно, и с увеличением числа Рейнольдса – толщина пограничного ламинарного слоя δ уменьшается.

Внутренняя поверхность трубы не может быть абсолютно гладкой и обладает некоторой шероховатостью Δ.

Шероховатость Δ - характеризуется средней высотой неровностей, шероховатость зависит от материала и технологии изготовления труб. Значение шероховатости обязательно указывается в паспорте на трубу.

В расчетах используются также величины относительной шероховатости и относительной гладкости .

Среднюю высоту неровностей стенок труб трудно измерить. Поэтому в гидравлических расчетах используется понятие эквивалентной шероховатости.

Эквивалентная шероховатость Δ_э - это некоторая близкая к средней величине высота выступов на внутренней поверхности трубы.

Если толщина вязкого слоя (рис. 2), то турбулентное ядро потока в процессе движения не соприкасается с неровностями стенок трубы. В этом случае коэффициент гидравлического трения не зависит от шероховатости, а стенки труб и сами трубы называются гидравлически гладкими.

 

Рис. 3. Гидравлически гладкие трубы.

 

Если (рис. 3), то турбулентное ядро потока соприкасается с неровностями стенок, λ зависит от шероховатости, а трубы называются гидравлически шероховатыми.

 

Рис. 3. Гидравлически шероховатые трубы.

Как известно, толщина ламинарного слоя зависит от числа Рейнольдса и уменьшается с его увеличением. Поэтому отнесение труб к разряду гидравлических гладких или шероховатых производится с помощью числа Рейнольдса.

Зависимость толщины ламинарного слоя от Re свидетельствует о том, что разделение труб на гладкие и шероховатые является условным. Труба, которая при небольшой скорости движения жидкости является гидравлически гладкой, может при увеличении скорости перейти в разряд шероховатых труб 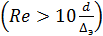и наоборот.

Гидравлически гладкими трубы являются при числах Рейнольдса в пределах 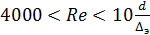. При гидравлически гладких трубах λ = f (Re) - коэффициент гидравлического трения λ зависит только от числа Рейнольдса. Потери напора по длине в гидравлически гладких трубах прямо пропорциональны средней скорости движения жидкости в степени 1,75.

Если 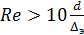, то труба относится к разряду гидравлически шероховатых труб (см. табл. 1). В гидравлически шероховатых трубах зависимость h _l от V меняется с изменением числа Рейнольдса.

Поэтому выделены области доквадратичного сопротивления шероховатых труб и квадратичного сопротивления шероховатых труб (см. табл.1).

При имеем область доквадратичного сопротивления, в которой h _l прямо пропорциональна скорости в степени от 1,75 до 2,00. В этой области λ = f (Re, Δ_э/d) - коэффициент гидравлического трения λ зависит как от шероховатости стенок труб, так и от числа Рейнольдса Re.

При имеем область квадратичного сопротивления, в которой h _l прямо пропорциональна квадрату скорости. В этой области наблюдается зависимость λ = f (Δ_э/d) - коэффициент гидравлического трения λ зависит только от характеристик самой трубы – внутреннего диаметра и шероховатости трубы, и не зависит от числа Рейнольдса Re.

Формулы для расчета коэффициента гидравлического трения при турбулентном режиме не удается получить теоретическим путем. Предложены десятки эмпирических формул. В табл. 1 приведены три из них, которые относятся к числу наиболее часто применяемых в практических расчетах.

 

Таблица 1