Задача № 11. Составить уравнение касательной и нормали кривой в данной точке
Решение: По формуле (41) имеем
или 
(*)
Находим координаты точки касания 
:
Затем определим производную от 
по 
, как от функции заданной параметрически, по формуле (43)
Вычислим ее значение для точки касания
.
Подставляя 
и 
в уравнение (*), получим
,
,
– уравнение касательной
или 
По формуле (42) имеем
или 
(**)
Подставляя и в уравнение (**), получим
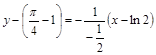
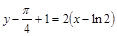– уравнение нормали
или 
Ответ: ,
Задача № 12. Найти асимптоты графика функции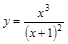 
.
Решение: Т.к. 
Следовательно, 
– вертикальная асимптота.
По формуле (46) находим
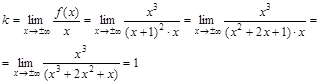
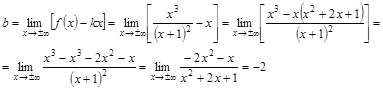
Таким образом, 
– наклонная асимптота графика функции.
Рассмотрим
(горизонтальной асимптоты нет)
Ответ:
.
Задача № 13. Провести полное исследование и построить график функции 
Решение: Воспользуемся планом полного исследования функции (см. § 5 главы III)
I. Функция определена на всей числовой оси кроме точки 
, т.е. 
1.
В точке функция имеет разрыв II-го рода, т.к. 
Аналогично рассматривается 
.
2. Функция является нечетной, т.к. 
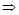график симметричен относительно начала координат, функция является непериодической.
3. Точек пересечения с осями координат нет.
II. Найдем асимптоты.
– вертикальная асимптота.
Для нахождения наклонных асимптот воспользуемся формулами (46)
Следовательно, уравнение наклонной асимптоты имеет вид 
.
Горизонтальной асимптоты нет, т.к. 
.
III. Находим производную первого порядка:
. Производная 
обращается в нуль при 
и не существует при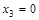 
. Однако, критическими точками являются только точки 
и 
: они лежат внутри области определения функции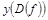 
и в них эта функция непрерывна. Точка 
.
Исследуем критические точки по знаку производной .
Следовательно, функция возрастает 
на 
, убывает 
на 
.
IV. Находим производную второго порядка
,
Имеем 
и 
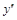не существует при , но 
Следовательно, точек перегиба нет.
Находим интервалы выпуклости функции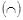 
и вогнутости 
:
 |
Т.е. функция выпукл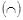а на 
и вогнута на 
.
V. Построим график функции
Задача № 14. Вычислить 
Решение:
.
Находим 
.
Находим смешанную производную
Ответ: 
.
Задача № 15. Найти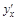 
, 
.
Решение:
Воспользуемся формулой (44):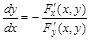 
.
Преобразуем уравнение к виду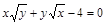 
, 
.
Находим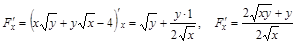 
Следовательно, 
,
.
Ответ:
Задача № 16. Найти наибольшее и наименьшее значения функции в замкнутой области 
.
, 
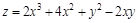Решение:
I. Ищем критические точки функции 
, лежащие внутри :
Решая систему уравнений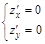 
, находим критические точки 
и 
. Ни одна из них не лежит внутри области . Других критических точек функция не имеет.
II. Находим наибольшее и наименьшее значения на границе заданной области.
а) На участке АОВ имеем 
, где 
.
Ищем наибольшее и наименьшее значения функции 
на отрезке 
:
1) 
; 
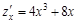при ; 
.
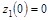2) Находим 
.
3) Сравнивая значения во внутренней критической точке и на концах 
, заключаем: наибольшее значение 
на отрезке равно 5, т.е. 
, а наименьшее значение на этом отрезке равно нулю (в точке ).
б) На участке АВ имеем 
где 
:
Ищем наибольшее и наименьшее значения 
на отрезке :
1) 
внутри данного отрезка 
при 
; 
.
2) Находим 
.
3) Наибольшее значение на отрезке равно 5 в точках 
, а наименьшее значение 
на этом отрезке равно 0,77 (в точке ).
Сопоставляя значения 
на участках АОВ и АВ, приходим к выводу: на всей границе наибольшее значение функции 
равно 5 (в точках А и В, а ее наименьшее значение равно 0 (в точке О).
III. Внутри заданной замкнутой области функция не имеет точек экстремума, ее наибольшее и наименьшее значения достигаются в точках, лежащих на границе этой области. В граничных точках 
и 
функция имеет наибольшее значение, 
, а в граничной точке 
она имеет наименьшее значение,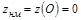 
.
