Занятие 3.Условные вероятности и независимые события.
Условные вероятности.
Пусть произведено 
испытаний (экспериментов, наблюдений), пусть событие 
произошло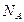 
раз, событие 
произошло 
раз, а оба события произошли в 
случаях. Наряду с 
- относительной частотой наступления события вычислим 
- относительную условную частоту наступления события , при условии, что произошло событие . Поскольку относительная частота колеблется вокруг вероятности события 
, получаем, что и 
.
Определение. Условная вероятность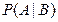 
события 
при условии, что событие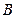 
произошло, определяется формулой 
, где 
.
Зафиксируем событие и наряду с 
рассмотрим 
- условное вероятностное пространство. Здесь множество элементарных исходов сужено до , система подмножеств 
является алгеброй, и 
по определению положим 
.
Условная вероятность 
удовлетворяет всем аксиомам и свойствам (безусловной) вероятности.
1. 
.
2. 
.
3. Если 
- объединение попарно несовместных событий из 
, то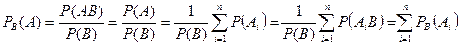 
.
Теорема умножения. Вероятность совместного наступления двух событий равна вероятности одного из них, умноженной на условную вероятность другого при условии, что первое событие наступило: 
.
Обобщая этот результат для вероятности произведения любого числа событий, получим: 
.
Пример 1. В урне 
белых и 
зеленых шаров. Опыт состоит в извлечении одного за другим двух шаров, причем: а) шары возвращаются; б) шары не возвращаются. Найдите вероятность извлечения двух зеленых шаров.
Решение.
а) 
;
б) 
.
Пример 2. Подбрасываются три игральные кости. Наблюдаемые события: 
, 
. Найти 
и 
.
Решение. По определению 
, 
.
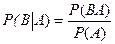Вычислим эти вероятности. Всего в опыте возможно 
исходов. Вычислим : 
, 
.
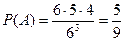Рассмотрим 
.
Тогда 
, 
, 
.
Рассмотрим 
.
, 
, 
.
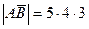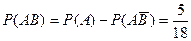Окончательно 
, 
.
Формулы полной вероятности и Байеса
Определение. Совокупностьсобытий 
называется полной группой событий, если 
, 
, 
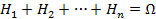. Сами события 
при этом называются гипотезами.
Теорема (формула полной вероятности).
Если - полная группа событий, то для любого события 
имеет место формула 
.
Доказательство. В условиях теоремы всякое событие можно разбить в сумму попарно несовместных событий 
: 
(см. рис.). Следовательно, 
. Каждое слагаемое можно расписать по формуле умножения 
.
Пример 3. В урне №1 имеется 6 белых и 2 черных шара, а в урне №2 - 4 белых и 4 черных. Из урны №1 в урну №2 наугад перекладывается один шар, после чего из урны №2 наугад выбирается шар. Какова вероятность, что будет выбран белый шар?
Решение. Пусть событие 
. Рассмотрим гипотезы: 
, 
.
Тогда 
, а 
. Вычислим условные вероятности:
, так как в урне номер два при гипотезе 
стало 5 белых шаров из 9, 
, так как при гипотезе 
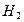число белых осталось равно 4 из 9.
Следовательно 
.
Теорема (формула Байеса).
Пусть гипотезы , 
, образуют полную группу событий и 
. Тогда имеет место формула: 
.
Доказательство. По формуле умножения вероятностей
, откуда после деления на вероятность
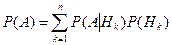и получается формула Байеса.
Вероятности 
называются апостериорными (вычисленными после опыта) вероятностями гипотез , в отличие от вероятностей 
, называемых априорными (известными до проведения опыта). То есть результат опыта (осуществление или неосуществление события ) позволяет уточнить вероятности гипотез.
Пример 4. Группа состоит из 
отличников, 
хорошистов и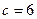 
слабых учеников. Отличники на предстоящем экзамене могут получить только отличные оценки, хорошисты с равной вероятностью "хорошо", "отлично" или "удовлетворительно", а остальные с равными вероятностями "удовлетворительно" и "неудовлетворительно". Для сдачи экзамена наугад вызывается один ученик. С какой вероятностью он получит "хорошо" или "отлично" (событие )?
Решение. Рассмотрим три гипотезы: 
, 
, 
.
Тогда 
, 
, 
.
Найдем условные вероятности: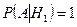 
, 
, 
. Тогда 
.
