Если заданный интеграл простейшим преобразованием трудно привести (или нельзя привести) к табличному интегралу, то для его отыскания применяют особые приемы. Один из них – интегрирование способом подстановки. Еще этот метод называют способом замены переменной.
Прежде чем перейти к рассмотрению способа подстановки, вспомним понятие дифференциала функции.
Определение. Если функция y(x) в точке 
имеет производную 
, то произведение 
является дифференциалом функции у(х) в точке и обозначается dy(
. Таким образом dy(
dx.
dy = 
|
Интегрирование способом подстановки заключается в том, что выражение заменяется новой переменной.
Например в интеграле 
необходимо произвести замену переменной. Обозначим 
. Найдем дифференциал обеих частей равенства: d(
Дифференциал данного в интеграле переменного значения необходимо выразить через дифференциал введенной нами переменной.
Имеем: 
(таким образом вторую часть подынтегрального выражения выразили через dt).
Замену подставляем в интеграл, и под знаком интеграла получаем выражение, зависящее только от введенной новой переменной t. Если замена проведена правильно, то полученный интеграл должен быть табличным. Таким образом, получаем: 
- ответ выражен через вспомогательную переменную t.
Чтобы получить окончательный ответ, сделаем обратную замену 
:
= 
Подстановка должна выбираться так: если одна часть подынтегрального выражения обозначается за t, то другая должна соответствовать dt с каким-нибудь коэффициентом. В нашем примере
t 
dt
|
|
Пример 1: 
. Произведем замену переменной: 2+x=t, dx=dt.
Пример 2. 
. Произведем замену: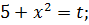 
.
Пример 3. 
. Произведем замену: 
Тогда интеграл примет вид: 
Пример 4. 
Произведем замену: 
Пример 5. 
. Произведем замену: 
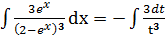= -3 
Пример 6. 
Произведем замену: sinx=t; cosxdx=dt
Пример 7. 
. Произведем замену: lnx=t; 
+C.
Задание №11.
| № | ЗАДАНИЕ | ВАРИАНТЫ ОТВЕТА |
| 1. | 
| 1) 
|
| 2. | 
| 1)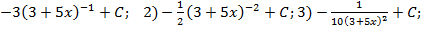 
4)- 
|
| 3. | 
| 1) 
|
| 4. | 
| 1)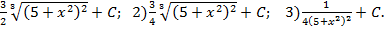 
|
| 5. | 
| 1) 
|
| 6. | 
| 1)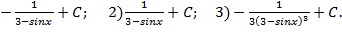 
|
| 7. | 
| 1) 
|
| 8. | 
| 1) 
|
 +C
|
|
Для того чтобы интеграл приводился к виду 
, он должен состоять из дроби, числитель которой равен дифференциалу знаменателя с некоторым коэффициентом. Выражение, стоящее в знаменателе, должно быть в первой степени, в противном случае интеграл соответствует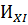 
. Подстановка делается так, что весь 
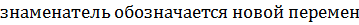ной.
Пример 1. 
. Произведем замену: 
.
= 
Пример 2. 
. Произведем замену: 1+3cosx=t; -3sinxdx=dt; sinxdx= 
dt. Тогда интеграл будет иметь вид: =- 
=- 
ln 
+C=
ln 
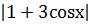+C.
Пример 3. 
. Произведем замену: 
= 
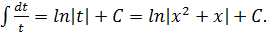
Задание №12.
| № | ЗАДАНИЕ | ВАРИАНТЫ ОТВЕТА |
| 1. | 
| 
|
| 2. | 
| 1) 
|
| 3. | 
| 1)-  +c; 3) –  +C.
|
| 4. | 
| 1) 
|
| 5. |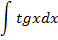 
| 1) 
|
|
|
Для того чтобы интеграл приводился к виду 
, он должен содержать показательную функцию с показателем вида f(x). Этот показатель и заменяется новой переменной.
Пример 1.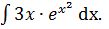 
Произведем замену: 
= 
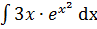Пример 2. 
Произведем замену: sinx=t; cosxdx=dt.
Пример 3. 
Произведем замену: 
.
Задание №13.
| № | ЗАДАНИЕ | ВАРИАНТЫ ОТВЕТА |
| 1. | 
| 1)  3)  .
|
| 2. | 
| 1) 
|
|
|
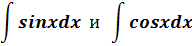
К 
приводятся интегралы, содержащие sinf(x) или cosf(x), где f(x) заменяется через новое переменное.
Пример 1. 
. Произведем замену: 
Пример 2. 
По известной Вам формуле: 
.
.
Во втором интеграле произведем замену: 2x=t; 2dx=dt; dx= 
.
Пример 3. 
.
Произведем замену в первом интеграле: 3x=t; 3dx=dt; dx= 
Произведем замену во втором интеграле: 2x=t; 2dx=dt; dx= 
Следовательно: 
Задание №14.
| № | ЗАДАНИЕ | ВАРИАНТЫ ОТВЕТА |
| 1. | 
| 1)-cos4x+C; 2) 
|
| 2. | 
| 1)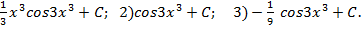 
|
| 3. | 
| 1)  .
|
ЗАДАНИЕ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
1. 
; 2. 
; 3. 
;
4. 
5. 
6. 
|
|
К 
приводятся интегралы, содержащие в знаменателе 
, поэтому f(x) заменяется через вспомогательное переменное.
Пример 1. 
. Произведем замену: 3x=t; 3dx=dt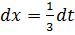 
.
Пример 2. 
. Произведем замену: 1-2x=t; -2dx=dt;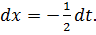 
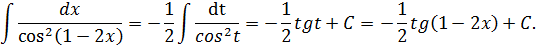
Пример 3. 
. Произведем замену: lnx=t; 
Пример 4. 
. Произведем замену: 
= -ctgt+C=-ctg 
Задание №15.
| № | ЗАДАНИЕ | ВАРИАНТЫ ОТВЕТА |
| 1. | 
| 1) tg2x+C; 2) 
|
| 2. | 
| 1)  tg  tg 
|
| 3. | 
| 1) 
|
|
|
К 
приводятся интегралы, содержащие в знаменателе корень их разности постоянной величины и квадрата х с некоторым коэффициентом или сумму постоянной величины и квадрата х с коэффициентом.
Пример 1. 
. Произведем замену: 
Пример 2. 
Произведем замену: 
= 
dt.
Пример 3. 
.Произведем замену: 
= 
= 
= 
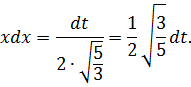
Задание №16.
| № | ЗАДАНИЕ | ВАРИАНТЫ ОТВЕТА |
| 1. | 
| 1)arctg3x+C; 2)  +C; 3) 
|
| 2. | 
| 1) 
|
| 3. | 
| 1) 
|
ЗАДАНИЕ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ
1. 
4. 
; 6. 
.
ТЕМА №3
Интегрирование по частям
|
Пусть U=U(x) и V=V(x) – дифференцируемые функции. По свойству дифференциала d(U·V)=VdU+UdV UdV=d(U·V)-VdU.
Интегрируем обе части равенства: 
Используя свойства неопределенного интеграла, получаем формулу интегрирования по частям для неопределенного интеграла:
|
При её применении фиксируется разбиение подынтегрального выражения искомого интеграла на два сомножителя U и dV. При переходе к правой части формулы первый из сомножителей дифференцируется (при нахождении дифференциала dU=U´dx), второй интегрируется (V= 
Возможности применения формулы интегрирования по частям связаны с тем, что дифференцирование может существенно упростить один из сомножителей (при условии, что интегрирование не слишком усложнит другой).
Пример 1. 
Так как x´=1, а 
при интегрировании практически не изменяется (появляется лишь постоянный множитель 
, то данный интеграл можно найти интегрированием по частям.
Пусть U=x; dV= 
, тогда dU=dx; 
k=-2; b=0 =- 
Применяя формулу интегрирования по частям, получаем:
Замечание: Анализ полученного решения показывает, что постоянная С, возникшая при нахождении V (по заданному dV), не входит в запись окончательного ответа. Аналогично, в общем случае постоянная С, возникшая при нахождении V, исключается в процессе решения. Поэтому в дальнейшем, применяя формулу интегрирования по частям и найдя V, будем полагать С=0, что несколько упрощает запись решения.
Пример 2.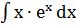 
.
Пусть U=x; dV= 
Тогда dU=dx; V= 
Пример 3. 
dx.
Пусть U=2+3x; dV= 
Тогда dU=d(2+3x)=(2+3x)´dx=3dx; V= 
.
Применяя формулу интегрирования по частям, получаем:
= 
Пример 4. 
U dV
Пусть arctgx=U; dx=dV
Тогда dU=(arctgx)´dx= 
Получаем согласно формулы интегрирования по частям:
=
= 
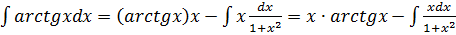Указание. Все интегралы, которые находят с использованием формулы интегрирования по частям, можно разбить на три группы.
I группа: 
, где P(x) –многочлен.
В данной группе полагаем U=lnx; U=arcsinx; U=arccosx; U=artgx; U=arcctgx, а оставшееся выражение за dV=P(x)dx.
II группа: 
, где Р(х)- многочлен, k и b-числа.
В данной группе полагаем U=P(x), а оставшееся выражение за dV.
III группа: 
.
Эта группа сложных интегралов. Они находятся при помощи двукратного интегрирования.
Пример 5. 
Пусть U=lnx; dV=xdx.
Тогда dU=d(lnx)= 
; V= 
.
Пример 6. 
.
Пусть U=lnx; dV= 
.
Тогда dU=d(lnx)= 
.
Применяя формулу интегрирования по частям, получаем:
.
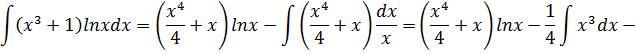
